The derivative of the function does not fall very far, and in the case of L'Hôpital's rules, it falls exactly to the same direction as the original function. This circumstance helps in disclosing uncertainties of the form 0/0 or ∞ / ∞ and some other uncertainties that arise when calculating limit the ratio of two infinitesimal or infinitely large functions. The calculation is greatly simplified with the help of this rule (in fact, two rules and notes to them):
As the formula above shows, when calculating the limit of the ratio of two infinitesimal or infinitely large functions, the limit of the ratio of two functions can be replaced by the limit of their ratio derivatives and thus get a certain result.
Let's move on to more precise formulations of L'Hôpital's rules.
L'Hôpital's rule for the case of the limit of two infinitesimal quantities... Let the functions f(x) and g(x a... And at the very point a a derivative of a function g(x) is not equal to zero ( g"(x a are equal to each other and equal to zero:
.
L'Hôpital's rule for the case of the limit of two infinitely large quantities... Let the functions f(x) and g(x) have derivatives (i.e., differentiable) in some neighborhood of the point a... And at the very point a they may or may not have derivatives. Moreover, in the vicinity of the point a derivative of a function g(x) is not equal to zero ( g"(x) ≠ 0) and the limits of these functions as x tends to the value of the function at the point a are equal to each other and equal to infinity:
.
Then the limit of the ratio of these functions is equal to the limit of the ratio of their derivatives:
In other words, for uncertainties of the form 0/0 or ∞ / ∞, the limit of the ratio of two functions is equal to the limit of the ratio of their derivatives, if the latter exists (finite, that is, equal to a certain number, or infinite, that is, equal to infinity).
Remarks.
1. L'Hôpital's rules are also applicable when the functions f(x) and g(x) are not defined for x = a.
2. If, when calculating the limit of the ratio of derivatives of functions f(x) and g(x) again we arrive at an uncertainty of the form 0/0 or ∞ / ∞, then L'Hôpital's rules should be applied multiple times (at least twice).
3. L'Hôpital's rules are also applicable when the argument of the functions (x) tends not to a finite number a, and to infinity ( x → ∞).
Uncertainties of other types can also be reduced to uncertainties of 0/0 and ∞ / ∞ types.
Disclosure of uncertainties of the types "zero divided by zero" and "infinity divided by infinity"
Example 1.
x= 2 results in an uncertainty of the form 0/0. Therefore, the derivative of each function and we obtain
The derivative of the polynomial was calculated in the numerator, and in the denominator - derivative of a complex logarithmic function... Before the last equal sign, the usual limit, substituting two instead of x.
Example 2. Calculate the limit of the ratio of two functions using L'Hôpital's rule:
Solution. Substitution of a value in a given function x
Example 3. Calculate the limit of the ratio of two functions using L'Hôpital's rule:
Solution. Substitution of a value in a given function x= 0 results in an uncertainty of the form 0/0. Therefore, we calculate the derivatives of the functions in the numerator and denominator and get:
Example 4. Calculate
Solution. Substitution of the x value equal to plus infinity into the given function leads to an uncertainty of the form ∞ / ∞. Therefore, we apply L'Hôpital's rule:
Comment. Let us turn to examples in which L'Hôpital's rule has to be applied twice, that is, to come to the limit of the ratios of the second derivatives, since the limit of the ratio of the first derivatives is an uncertainty of the form 0/0 or ∞ / ∞.
Disclosure of uncertainties of the form "zero times infinity"
Example 12. Calculate
.
Solution. We get
This example uses trigonometric identity.
Disclosure of uncertainties of the types "zero to the power of zero", "infinity to the power of zero" and "one to the power of infinity"
Uncertainties of the form, or are usually reduced to the form 0/0 or ∞ / ∞ using the logarithm of a function of the form
To calculate the limit of an expression, one should use the logarithmic identity, a special case of which is the property of the logarithm 
.
Using the logarithmic identity and the continuity property of the function (to go beyond the limit sign), the limit should be calculated as follows:
Separately, you should find the limit of expression in the exponent and build e to the degree found.
Example 13.
Solution. We get
.
.
Example 14. Calculate using L'Hôpital's rule
Solution. We get
We calculate the limit of expression in the exponent
.
.
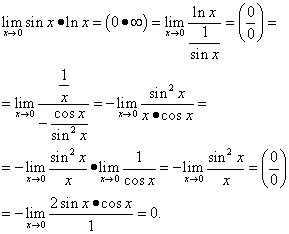Example 15. Calculate using L'Hôpital's rule
Uncertainties of type and type are the most common uncertainties that need to be disclosed when solving limits.
Most of the tasks to the limits that come across to students, just carry such uncertainties. To reveal them, or, more precisely, to avoid ambiguities, there are several artificial methods for transforming the form of an expression under the limit sign. These techniques are as follows: term-by-term division of the numerator and denominator by the highest power of the variable, multiplication by the conjugate expression and factorization for subsequent reduction using solutions of quadratic equations and abbreviated multiplication formulas.
Uncertainty of the species
Example 1.
n is equal to 2. Therefore, we divide the numerator and denominator by term:
.
Comment on the right side of the expression. Arrows and numbers indicate what the fractions tend to after substitution instead of n infinity values. Here, as in example 2, the degree n more in the denominator than in the numerator, as a result of which the whole fraction tends to an infinitely small value or "super-small number".
We get the answer: the limit of this function with a variable tending to infinity is equal to.
Example 2. .
Solution. Here the highest power of the variable x is equal to 1. Therefore, we divide the numerator and denominator by term x:
.
Commentary on the course of the solution. In the numerator, we drive "x" under the root of the third degree, and so that its initial degree (1) remains unchanged, we assign it the same degree as that of the root, that is, 3. There are no more arrows and additional numbers in this entry, so try mentally, but by analogy with the previous example, determine what the expressions in the numerator and denominator are striving for after substituting infinity for "x".
We got the answer: the limit of this function with a variable tending to infinity is equal to zero.
Uncertainty of the species
Example 3. Uncover uncertainty and find a limit.
Solution. The numerator is the difference between the cubes. Let's factor it out using the formula of abbreviated multiplication from the school mathematics course:
The denominator is a quadratic trinomial, which we factor out by solving a quadratic equation (once again a reference to solving quadratic equations):
Let's write the expression obtained as a result of the transformations and find the limit of the function:
Example 4. Uncover uncertainty and find the limit
Solution. The quotient limit theorem is not applicable here, since
Therefore, we transform the fraction identically: multiplying the numerator and denominator by the binomial conjugate to the denominator, and cancel it by x+1. According to the corollary to Theorem 1, we obtain an expression, solving which, we find the desired limit:
Example 5. Uncover uncertainty and find the limit
Solution. Direct value substitution x= 0 to the given function results in an uncertainty of the form 0/0. To reveal it, we perform identical transformations and get the desired limit as a result: 
Example 6. Calculate 
Solution: we use the theorems on the limits
Answer: 11
Example 7. Calculate 
Solution: in this example, the limits of the numerator and denominator are 0:
; 
... We have obtained, therefore, the theorem on the limit of the quotient cannot be applied.
Let us factor out the numerator and denominator to cancel the fraction by a common factor tending to zero, and, therefore, to make possible the application of Theorem 3.
We expand the square trinomial in the numerator by the formula, where x 1 and x 2 are the roots of the trinomial. Having factorized and denominated, cancel the fraction by (x-2), then apply Theorem 3.
Answer:
Example 8. Calculate
Solution: At, the numerator and denominator tend to infinity; therefore, with the direct application of Theorem 3, we obtain an expression that represents an uncertainty. To get rid of this kind of ambiguity, divide the numerator and denominator by the highest degree of the argument. In this example, you need to divide by X:
Answer:
Example 9. Calculate 
Solution: x 3:
Answer: 2
Example 10. Calculate 
Solution: When the numerator and denominator tend to infinity. Divide the numerator and denominator by the highest degree of the argument, i.e. x 5:
= 
the numerator of the fraction tends to 1, the denominator to 0, so the fraction tends to infinity.
Answer:
Example 11. Calculate
Solution: When the numerator and denominator tend to infinity. Divide the numerator and denominator by the highest degree of the argument, i.e. x 7:
Answer: 0
Derivative.
Derivative of the function y = f (x) with respect to the argument x is the limit of the ratio of its increment y to the increment x of the argument x when the increment of the argument tends to zero:. If this limit is finite, then the function y = f (x) is called differentiable at the point x. If this limit exists, then they say that the function y = f (x) has an infinite derivative at the point x.
Derivatives of basic elementary functions:
1. (const) = 0 9. 
3. 11. 
4. 
12. 
5. 13. 
6. 
14. 
Differentiation rules:
a) 
v) 
Example 1. Find the derivative of a function 
Solution: If the derivative of the second term is found according to the rule of differentiation of the fraction, then the first term is a complex function, the derivative of which is found by the formula:
, where 
, then
When solving the formulas were used: 1,2,10, a, c, d.
Answer:
Example 21. Find the derivative of a function 
Solution: both terms are complex functions, where for the first, and for the second,, then
Answer: 
Derivative applications.
1. Speed and acceleration
Let the function s (t) describe position object in a certain coordinate system at time t. Then the first derivative of the function s (t) is instantaneous speed object:
v = s ′ = f ′ (t)
The second derivative of the function s (t) is the instantaneous acceleration object:
w = v ′ = s ′ ′ = f ′ ′ (t)
2. Tangent equation
y − y0 = f ′ (x0) (x − x0),
where (x0, y0) are the coordinates of the point of tangency, f ′ (x0) is the value of the derivative of the function f (x) at the point of tangency.
3. Normal Equation
y − y0 = −1f ′ (x0) (x − x0),
where (x0, y0) are the coordinates of the point at which the normal is drawn, f ′ (x0) is the value of the derivative of the function f (x) at this point.
4. Increasing and decreasing functions
If f ′ (x0)> 0, then the function increases at the point x0. In the figure below, the function is increasing as x
If f ′ (x0)<0, то функция убывает в точке x0 (интервал x1
5. Local extrema of a function
The function f (x) has local maximum at the point x1 if there exists a neighborhood of the point x1 such that the inequality f (x1) ≥f (x) holds for all x from this neighborhood.
Similarly, the function f (x) has local minimum at the point x2 if there exists a neighborhood of the point x2 such that for all x from this neighborhood the inequality f (x2) ≤f (x) holds.
6. Critical points
Point x0 is critical point function f (x) if the derivative f ′ (x0) in it is equal to zero or does not exist.
7. The first sufficient indicator of the existence of an extremum
If the function f (x) increases (f ′ (x)> 0) for all x in some interval (a, x1] and decreases (f ′ (x)<0) для всех x в интервале и возрастает (f′(x)>0) for all x from the interval ^ \ infty $ and $ ^ \ infty $.
Also, such uncertainties can be disclosed using the logarithm of the exponential function, but this is a different solution method, which will be covered in another article.
Formula and Consequences
Formula the second remarkable limit is written as follows: $$ \ lim_ (x \ to \ infty) \ bigg (1+ \ frac (1) (x) \ bigg) ^ x = e, \ text (where) e \ approx 2.718 $$
The formula implies consequences, which are very convenient to use for solving examples with limits: $$ \ lim_ (x \ to \ infty) \ bigg (1 + \ frac (k) (x) \ bigg) ^ x = e ^ k, \ text (where) k \ in \ mathbb (R) $$ $$ \ lim_ (x \ to \ infty) \ bigg (1 + \ frac (1) (f (x)) \ bigg) ^ (f (x)) = e $ $ $$ \ lim_ (x \ to 0) \ bigg (1 + x \ bigg) ^ \ frac (1) (x) = e $$
It is worth noting that the second remarkable limit can be applied not always to the exponential function, but only in cases where the base tends to unity. To do this, first, the base limit is calculated in the mind, and then conclusions are drawn. All of this will be covered in the sample solutions.
Examples of solutions
Let's consider examples of solutions using a direct formula and its consequences. We will also analyze the cases in which the formula is not needed. It is enough to write down only the ready-made answer.
| Example 1 |
| Find the limit $ \ lim_ (x \ to \ infty) \ bigg (\ frac (x + 4) (x + 3) \ bigg) ^ (x + 3) $ |
| Solution |
|
Let's substitute infinity in the limit and look at the uncertainty: $$ \ lim_ (x \ to \ infty) \ bigg (\ frac (x + 4) (x + 3) \ bigg) ^ (x + 3) = \ bigg (\ frac (\ infty) (\ infty) \ bigg) ^ \ infty $$ Find the limit of the base: $$ \ lim_ (x \ to \ infty) \ frac (x + 4) (x + 3) = \ lim_ (x \ to \ infty) \ frac (x (1+ \ frac (4) ( x))) (x (1+ \ frac (3) (x))) = 1 $$ We got a base equal to one, which means that the second remarkable limit can already be applied. To do this, we fit the base of the function to the formula by subtracting and adding one: $$ \ lim_ (x \ to \ infty) \ bigg (1 + \ frac (x + 4) (x + 3) - 1 \ bigg) ^ (x + 3) = \ lim_ (x \ to \ infty) \ bigg (1 + \ frac (1) (x + 3) \ bigg) ^ (x + 3) = $$ We look at the second consequence and write down the answer: $$ \ lim_ (x \ to \ infty) \ bigg (1 + \ frac (1) (x + 3) \ bigg) ^ (x + 3) = e $$ If you can't solve your problem, then send it to us. We will provide a detailed solution. You will be able to familiarize yourself with the course of the calculation and get information. This will help you get credit from your teacher in a timely manner! |
| Answer |
| $$ \ lim_ (x \ to \ infty) \ bigg (1 + \ frac (1) (x + 3) \ bigg) ^ (x + 3) = e $$ |
| Example 4 |
| Solve limit $ \ lim_ (x \ to \ infty) \ bigg (\ frac (3x ^ 2 + 4) (3x ^ 2-2) \ bigg) ^ (3x) $ |
| Solution |
|
We find the limit of the base and see that $ \ lim_ (x \ to \ infty) \ frac (3x ^ 2 + 4) (3x ^ 2-2) = 1 $, so the second wonderful limit can be applied. Standardly, according to the plan, we add and subtract one from the base of the degree: $$ \ lim_ (x \ to \ infty) \ bigg (1+ \ frac (3x ^ 2 + 4) (3x ^ 2-2) -1 \ bigg) ^ (3x) = \ lim_ (x \ to \ infty ) \ bigg (1+ \ frac (6) (3x ^ 2-2) \ bigg) ^ (3x) = $$ We fit the fraction to the formula of the 2nd remark. limit: $$ = \ lim_ (x \ to \ infty) \ bigg (1+ \ frac (1) (\ frac (3x ^ 2-2) (6)) \ bigg) ^ (3x) = $$ Now let's adjust the degree. The power must be a fraction equal to the denominator of the base $ \ frac (3x ^ 2-2) (6) $. To do this, multiply and divide the degree by it, and continue to solve: $$ = \ lim_ (x \ to \ infty) \ bigg (1+ \ frac (1) (\ frac (3x ^ 2-2) (6)) \ bigg) ^ (\ frac (3x ^ 2-2) (6) \ cdot \ frac (6) (3x ^ 2-2) \ cdot 3x) = \ lim_ (x \ to \ infty) e ^ (\ frac (18x) (3x ^ 2-2)) = $$ The limit located in degree at $ e $ is: $ \ lim_ (x \ to \ infty) \ frac (18x) (3x ^ 2-2) = 0 $. Therefore, continuing the solution, we have: |
| Answer |
| $$ \ lim_ (x \ to \ infty) \ bigg (\ frac (3x ^ 2 + 4) (3x ^ 2-2) \ bigg) ^ (3x) = 1 $$ |
Let us examine the cases when the problem is similar to the second remarkable limit, but it can be solved without it.
In the article: "The second remarkable limit: examples of solutions" was analyzed the formula, its consequences, and given the frequent types of problems on this topic.
CONSPECT 20
20.1 UNCERTAINTY DISCLOSURE
Example 1
Solve the limit 
First, let's try to substitute -1 in the fraction: 
In this case, the so-called uncertainty is obtained.
General rule: if there are polynomials in the numerator and denominator, and there are uncertainties of the form, then for its disclosure you need to factor out the numerator and denominator.
To do this, most often you need to solve a quadratic equation and / or use abbreviated multiplication formulas.
Factor out the numerator. 
Example 2
Calculate Limit 
Let us factor out the numerator and denominator.
Numerator denominator: 
,
The method of multiplying the numerator and denominator by the conjugate expression
We continue to consider the uncertainty of the form
The next type of limits is similar to the previous type. The only thing, besides the polynomials, we will add roots.
Example 3
Find the limit 
Multiply the numerator and denominator by the conjugate expression.
20.2 UNCERTAINTY DISCLOSURE
Now we will consider a group of limits when, and the function is a fraction, in the numerator and denominator of which there are polynomials
Example 4
Calculate Limit 
According to our rule, we will try to substitute infinity into the function. What do we get at the top? Infinity. And what happens below? Also infinity. So we have the so-called uncertainty of the species. One would think that, and the answer is ready, but in the general case this is not at all the case, and you need to apply some solution technique, which we will now consider.
How to solve limits of a given type?
First, we look at the numerator and find in the highest power: 
The highest degree in the numerator is two.
Now we look at the denominator and also find in the highest power: 
The highest power of the denominator is two.
Then we choose the highest power of the numerator and denominator: in this example, they are the same and equal to two.
So, the solution method is as follows: in order to uncover uncertaintyit is necessary to divide the numerator and denominator byin the senior degree.
Divide the numerator and denominator by 
That's how it is, the answer, not infinity.
What is fundamentally important in the design of the solution?
First, we indicate the uncertainty, if any.
Second, it is advisable to interrupt the solution for intermediate explanations. I usually use a sign, it does not carry any mathematical meaning, but means that the solution was interrupted for an intermediate explanation.
Thirdly, in the limit it is desirable to mark what is striving and where. When the work is completed by hand, it is more convenient to do it like this: 
It is best to use a simple pencil to mark up.
Of course, you can do nothing of this, but then, perhaps, the teacher will note the shortcomings in the solution or start asking additional questions on the assignment. Do you need it?
Example 5
Find the limit 
Again, in the numerator and denominator, we find in the highest power: 
Maximum degree in the numerator: 3 Maximum degree in the denominator: 4 Select the greatest value, in this case a four. According to our algorithm, to disclose the uncertainty, we divide the numerator and the denominator by. The complete design of the assignment may look like this:
Example 6
Find the limit 
The maximum degree of "x" in the numerator: 2 The maximum degree of "x" in the denominator: 1 (can be written as) To disclose the uncertainty, it is necessary to divide the numerator and the denominator by. A clean solution might look like this:
Divide the numerator and denominator by
Recording does not mean division by zero (you cannot divide by zero), but division by an infinitesimal number.
Thus, when disclosing the uncertainty of the species, we can get finite number, zero or infinity.
PRACTICE 20
JOB N 1
Solution: If, instead of the variable, we put the value 7, to which it tends, then we get the uncertainty of the form, then 
JOB N 2Topic: Disclosure of Zero to Zero Uncertainty
Solution: If, instead of the variable, we put the value 0, to which it tends, then we get the uncertainty of the form, then
JOB # 3Topic: Disclosure of Zero to Zero Uncertainty
Solution: If instead of the variable we put the value 6, to which it tends, then we get the uncertainty of the form, then
JOB # 4
Solution: Because 
and 
JOB # 5Topic: Disclosure of uncertainty of the form "infinity to infinity"
Solution: Because 
and 
then there is an uncertainty of the form To reveal it, you need to divide each term of the numerator and denominator by. Then, knowing that we will receive: 
INDEPENDENT WORK 20
JOB N 1Topic: Disclosure of Zero to Zero Uncertainty
JOB N 2Topic: Disclosure of Zero to Zero Uncertainty
JOB # 3Topic: Disclosure of Zero to Zero Uncertainty
JOB # 4Topic: Disclosure of uncertainty of the form "infinity to infinity"
JOB # 5Topic: Disclosure of uncertainty of the form "infinity to infinity" Function limit 
equals ...
JOB # 6Topic: Disclosure of uncertainty of the form "infinity to infinity"
Methods for solving the limits. Uncertainties.
The growth order of the function. Replacement method
Example 4
Find the limit 
This is a simpler example for a do-it-yourself solution. In the proposed example, there is again uncertainty (of a higher order of growth than the root).
If "x" tends to "minus infinity"
The ghost of "minus infinity" has been in this article for a long time. Consider the limits with polynomials in which. The principles and methods of solution will be exactly the same as in the first part of the lesson, with the exception of a number of nuances.
Consider 4 chips that will be required to solve practical tasks:
1) Calculate the limit 
The value of the limit depends only on the term, since it has the highest growth order. If, then infinitely large modulo negative number to the EVEN power, in this case - in the fourth, equal to "plus infinity":. Constant ("two") positive, That's why: 
2) Calculate the limit 
Here again the senior degree even, That's why: . But in front of the "minus" ( negative constant -1), therefore: 
3) Calculate the limit 
The limit value depends only on. As you remember from school, the "minus" "jumps out" from under the odd degree, therefore infinitely large modulo negative number to odd power equals "minus infinity", in this case:.
Constant ("four") positive, means: 
4) Calculate the limit
The first guy in the village has again odd degree, moreover, in the bosom negative constant, which means: Thus:
.
Example 5
Find the limit 
Using the above points, we come to the conclusion that there is uncertainty. The numerator and denominator are of the same order of growth, which means that in the limit you get a finite number. Let's find out the answer, discarding all the fry: 
The solution is trivial: 
Example 6
Find the limit 
This is an example for a do-it-yourself solution. Complete solution and answer at the end of the tutorial.
And now, perhaps the most subtle of the cases:
Example 7
Find the limit 
Considering the leading terms, we come to the conclusion that there is uncertainty. The numerator is of a higher order of growth than the denominator, so you can immediately say that the limit is infinity. But which infinity, plus or minus? The technique is the same - in the numerator and denominator, we get rid of the little things: 
We decide: 
Divide the numerator and denominator by
Example 15
Find the limit
This is an example for a do-it-yourself solution. A rough example of finishing at the end of the lesson.
A couple more interesting examples on variable replacement:
Example 16
Find the limit
When substituting a unit in the limit, uncertainty is obtained. Variable replacement is already obvious, but first we transform the tangent using the formula. Indeed, why do we need a tangent?
Note that, therefore. If not entirely clear, look at the sine values in trigonometric table... Thus, we immediately get rid of the multiplier, in addition, we get the more familiar 0: 0 uncertainty. It would also be nice if the limit tends to zero.
Let's replace:
If, then
Under the cosine we have "x", which must also be expressed through "te".
From the replacement we express:.
We complete the solution: 
(1) We perform the substitution
(2) Expand the brackets under the cosine.
(4) To organize first wonderful limit, artificially multiply the numerator by and the reciprocal.
Assignment for independent solution:
Example 17
Find the limit
Complete solution and answer at the end of the tutorial.
These were not difficult tasks in their class, in practice everything can be worse, and, in addition to reduction formulas, you have to use a variety of trigonometric formulas, as well as other tricks. In the article Difficult Limits, I took apart a couple of real examples =)
On the eve of the holiday, let us finally clarify the situation with one more widespread uncertainty:
Elimination of uncertainty "one to the degree of infinity"
This uncertainty is "served" second wonderful limit, and in the second part of that lesson, we examined in great detail the standard examples of solutions that in most cases are encountered in practice. Now the picture with the exhibitors will be completed, in addition, the final tasks of the lesson will be devoted to the limits-"trick", in which it SEEMS that it is necessary to apply the 2nd wonderful limit, although this is not at all the case.
The disadvantage of the two working formulas of the 2nd remarkable limit is that the argument must tend to "plus infinity" or to zero. But what if the argument tends to a different number?
A universal formula comes to the rescue (which is actually a consequence of the second remarkable limit):
Uncertainty can be eliminated by the formula:
Somewhere like already explained what square brackets mean. Nothing special, brackets are like brackets. They are usually used to make a mathematical notation clearer.
Let's highlight the essential points of the formula:
1) It is only about uncertainty and no other.
2) The "x" argument may tend to arbitrary value(and not only to zero or), in particular, to "minus infinity" or to any a finite number.
Using this formula, you can solve all the examples of the lesson. Wonderful limits which belong to the 2nd remarkable limit. For example, let's calculate the limit:
In this case 
, and by the formula 
:
True, I do not advise you to do this, in the tradition it is still to use the "usual" design of the solution, if it can be applied. but using a formula is very convenient to check"Classic" examples at the 2nd remarkable limit.
