Пример 1. Определить напряженность и потенциал поля бесконечной плоскости, равномерно заряженной с поверхностной плотностью заряда s. Диэлектрическая проницаемость окружающей среды e.
Из симметрии задачи ясно, что линии напряженности электрического поля должны быть параллельными прямыми, перпендикулярными заряженной поверхности, как показано на ри с.1.2. Следовательно, поле заряженной плоскости является однородным.
Выберем замкнутую поверхность в виде прямого цилиндра длиной l с площадью основания S , как показано на рисунке. В силу однородности поля напряженности на нижнем и верхнем основаниях цилиндра одинаковы по величине и совпадают по направлению с положительными нормалями к этим поверхностям. Кроме того, учтем, что поток вектора напряженности через боковую поверхность отсутствует. Поэтому
Полный заряд в объеме, ограниченном цилиндрической поверхностью, равен q = sS . Тогда и .
Потенциал поля плоскости .
В полученном выражении С – постоянная интегрирования, а ось Ох перпендикулярна плоскости. Принимая потенциал на поверхности плоскости равным нулю, получаем С = 0.
Окончательно .
Пример 2. Определить напряженность и потенциал электрического поля бесконечной нити, равномерно заряженной с линейной плотностью заряда t. Диэлектрическая проницаемость окружающей среды e.
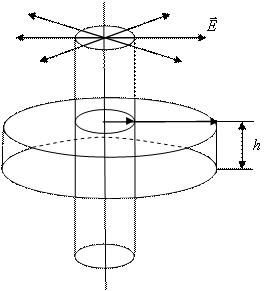
Из осевой симметрии задачи следует, что силовые линии поля нити представляют собой систему радиальных лучей, выходящих из точек, принадлежащих оси симметрии. Тогда в точках, равноудаленных от нити, напряженность поля одинакова по величине. Выберем в качестве замкнутой поверхности прямой цилиндр длины l с радиусом основания r , ось которого совпадает с нитью (см. рис.1.3). При этом поток вектора напряженности через основания цилиндра отсутствует, и полный поток через замкнутую поверхность равен потоку через боковую поверхность цилиндра s :
Т.к. в каждой точке боковой поверхности цилиндра направление совпадает с направлением нормали в этой точке, и E(r) = const , то
Полный заряд, заключенный в объеме цилиндра, q = tl . Тогда получаем
Потенциал поля нити
глее постоянная С определяется выбором точки нулевого потенциала
Пример 3. Шар радиуса R со сферической полостью радиуса а в центре заряжен с плотностью заряда, изменяющейся по линейному закону r = a(r – а), где a - постоянная величина, а r – расстояние от центра шара. Определить напряженность и потенциал электрического поля шара. Диэлектрическую проницаемость шара и окружающей среды принять равными 1.
Из сферической симметрии задачи следует, что напряженность электрического поля зависит только от расстояния r от центра шара, т.е. E = E(r) , а линии вектора - радиальные лучи, выходящие из начала координат, совмещенного с центром шара. При этом на любой сферической поверхности r = const напряженность поля по величине одинакова в каждой точке этой поверхности, а направление совпадает с направлением нормали к поверхности. Поэтому при использовании теоремы Гаусса в качестве замкнутой поверхности удобно выбирать поверхность r = const .
Рассмотрим поток вектора напряженности электрического поля через сферическую поверхность r < a . Т.к. в объеме полости заряд отсутствует, то поток вектора напряженности электрического поля через сферическую поверхность r < a равен 0, и, следовательно, электрическое поле в полости отсутствует.
Пусть радиус поверхности, через которую рассчитывается поток вектора напряженности, удовлетворяет неравенству a < r < R . Тогда поток вектора напряженности
С другой стороны этот поток с точностью до e 0 равен заряду, заключенному в объеме сферического слоя, ограниченного сферами радиусов а и r :
Таким образом,
И при a < r < R .
Рассмотрим поток вектора напряженности электрического поля через поверхность сферы r > R . Здесь, по-прежнему, N = , а заряд, заключенный в рассматриваемом объеме, равен полному заряду шара, т.е.
Поэтому при r > R .
Вычислим потенциал шара. Т.к. и при r < a Е = 0, то j 1 = С 1 ,
причем С 1 – постоянная. В области a < r < R
Вопрос из ОРОКСА
Две линии напряженности электрического поля не могут пересекаться в одной точке. Можно ли утверждать, что две эквипотенциальные поверхности также не могут пересекаться в одной точке?
Ответ: Две эквипотенциальные поверхности могут пересекаться в одной точке при условии, что напряженность поля в этой точке равна нулю. В самом деле, вектор напряженности определяет направление нормали к каждой эквипотенциальной поверхности. Так как поверхности пересекаются, в точке пересечения их нормали не совпадают, а значит, электрическое поле не может иметь определенного направления. Это возможно только при нулевом значении величины поля.
Компьютерная модель демонстрирует картину силовых линий и эквипотенциальных поверхностей точечного заряда и системы из двух точечных зарядов. Можно изменять величины зарядов и их знаки, а также расстояние между зарядами. При установке курсора в любой точке и нажатии левой клавиши мыши компьютер высвечивает на дисплее значения модуля вектора напряженности электрического поля и потенциала φ в данной точке. Следует обратить внимание, что в электрическом поле двух точечных зарядов возможны сферические эквипотенциальные поверхности.
2.7. Примеры вычисления потенциала
Рассмотрим вычисление потенциала поля, созданного некоторыми заряженными телами.
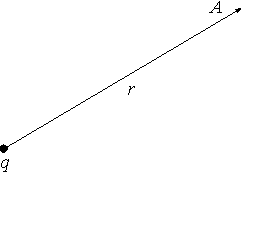
Рис.3. Расположение точки наблюдения А по отношению к точечному источнику поля q
1 .Пример Точечный заряд. Используя соотношения (1) и (4) и совмещая точку 1 с точкой наблюдения А (рис.3), а точку 2 удаляя на бесконечность, получим
Замечание. До сих пор использовалось понятие векторного поля - поля векторов (каждой точке пространства ставится в соответствие вектор ). Представление о потенциале как функции точки пространства позволяет ввести понятие скалярного поля - поля чисел (каждой точке пространства ставится в соответствие, с точностью до произвольной аддитивной постоянной, число ). Поэтому в дальнейшем кроме понятий электростатическое поле и поле , будем использовать понятие поля.
2.Пример . Найдем потенциал бесконечной однородно заряженной с линейной плотностью нити.
Наша задача найти как функцию .
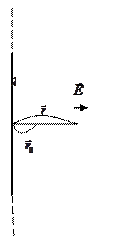
 Как уже было показано для бесконечно длинной нити:.
Как уже было показано для бесконечно длинной нити:.
Выберем где-нибудь точку из которой мы стартуем, к примеру в точке , то
![]() .
.
Договоримся, что в точке старта потенциал равен нулю: , тогда
![]() .
.
Это при такой нормировке. Если в такой задаче нормировать , то получим ,то есть все потенциалы во всех точках бесконечно большие. Кому нужна такая нормировка? Если Вас интересует какой-то конкретный пространственный диапазон, то нормировать надо где-то вблизи этой области, тогда все потенциалами будут конечными приятными числами. От бесконечной нити нельзя уйти на бесконечность, по этой же причине не следует ожидать хорошего результата от как суммы потенциалов точечных фрагментов нити, каждый из которых нормирован условием.
3.Пример . Потенциал поля точечного диполя (первый способ).
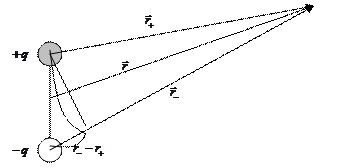 Итак, мы рассматриваем точечный диполь и точку наблюдения достаточно далеко от этой нашей гантельки.
Итак, мы рассматриваем точечный диполь и точку наблюдения достаточно далеко от этой нашей гантельки.
Давайте искать потенциал этой точки наблюдения.
Во первых, принцип суперпозиции.
Во-вторых, как известно
Учтя, что есть проекция вектора на и то, что расстояние до диполя очень велико, то
Потенциал поля точечного диполя (второй способ).
Используем готовую формулу для напряженности поля:
![]() . Вот такое выражение мы с вами в свое время вывели. Обопремся на него.
. Вот такое выражение мы с вами в свое время вывели. Обопремся на него.
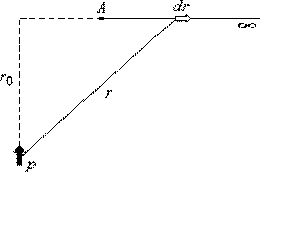
 Давайте выберем такое направление, чтобы нам было удобно вычислять этот интеграл, так как поле потенциальное, то результат не будет зависеть от вида траектории. Ориентация диполя, направление движения и вектор показаны на рисунке. С учетом некоторых соотношений (5) примет вид.
Давайте выберем такое направление, чтобы нам было удобно вычислять этот интеграл, так как поле потенциальное, то результат не будет зависеть от вида траектории. Ориентация диполя, направление движения и вектор показаны на рисунке. С учетом некоторых соотношений (5) примет вид.
Рассмотрим поле, созданное зарядом, равномерно распределенным по бесконечной нити. Эту задачу мы решили на прошлой лекции, воспользовавшись принципом суперпозиции электрических полей (см. 1.11).
Теперь покажем, несколько проще можно рассчитать это поле с помощью теоремы Гаусса.
Определим напряжённость поля на расстоянии r от нити, заряженной с постоянной линейной плотностью:
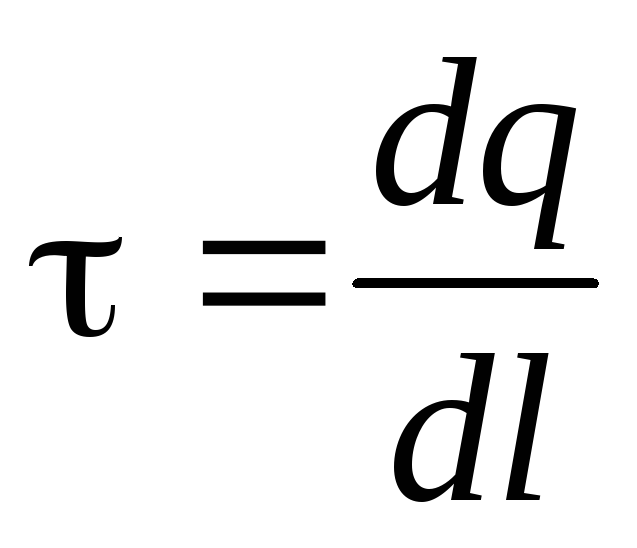 ,
[Кл/м] (2.10)
,
[Кл/м] (2.10)
Окружим нить замкнутой цилиндрической поверхностью (рис. 2.7.). Высота цилиндра - h , а радиус его основания -r .
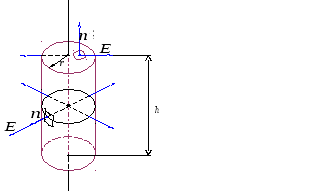
Рис. 2.7.
Поле, созданное заряженной нитью,
обладает цилиндрической симметрией. В
связи с этим векторы напряжённости во
всех точках боковой поверхности цилиндра
будут одинаковы по модулю и направлены
радиально, то есть перпендикулярно к
боковой поверхности цилиндра. На
основаниях цилиндра векторы
 ,
направленные по-прежнему радиально,
«скользят» по основанию, образуя прямой
угол с нормалью
,
направленные по-прежнему радиально,
«скользят» по основанию, образуя прямой
угол с нормалью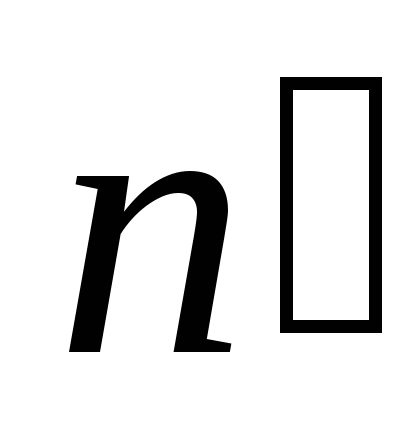 .
.
Вычислим поток вектора
 через поверхность выбранного цилиндра.
Полный поток через эту замкнутую
«гауссову» поверхность складывается
из потока через боковую поверхность
цилиндра и через два его основания:
через поверхность выбранного цилиндра.
Полный поток через эту замкнутую
«гауссову» поверхность складывается
из потока через боковую поверхность
цилиндра и через два его основания:
Последние два интеграла равны нулю, так
как «скользящие» по основаниям цилиндра
векторы
 не пронизывают их и не создают никакого
потока. Формально эти два интеграла
равны нулю, так как между векторами
не пронизывают их и не создают никакого
потока. Формально эти два интеграла
равны нулю, так как между векторами и
и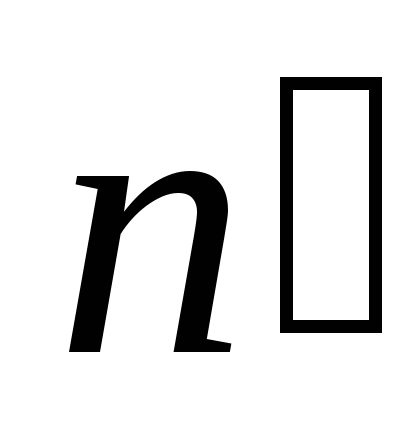 прямой угол и
прямой угол и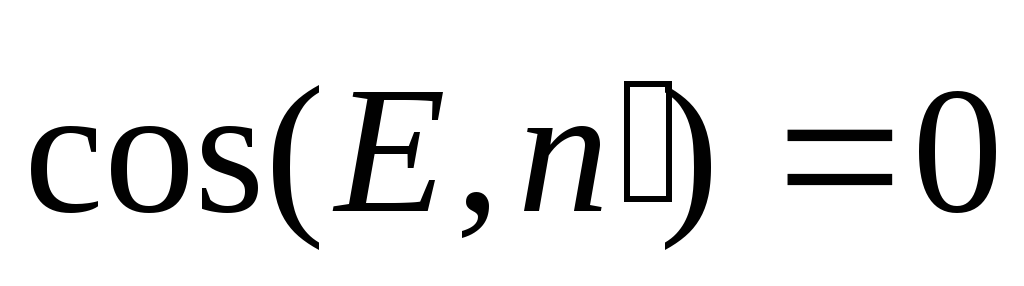 .
Таким образом
.
Таким образом
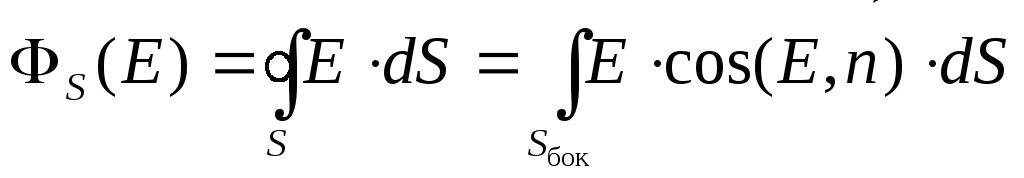
Во всех точках боковой поверхности
цилиндра E
=Е
r
=constи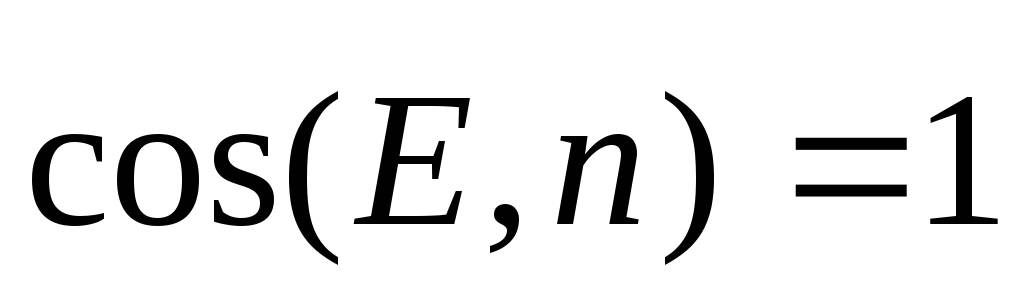 .
.
Поэтому поток через боковую поверхность цилиндра равен
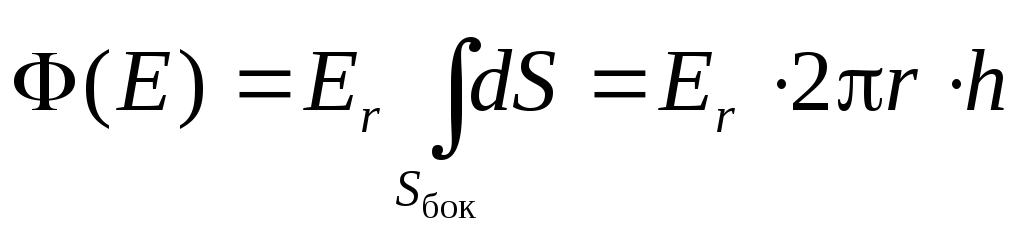 (2.11)
(2.11)
Это поток вектора напряжённости электрического поля, вычисленный по определению потока.
Теперь воспользуемся теоремой Гаусса, отметив предварительно, что «заряд, заключённый внутри гауссовой поверхности» в данном случае сосредоточен на отрезке нити h - на оси цилиндра:
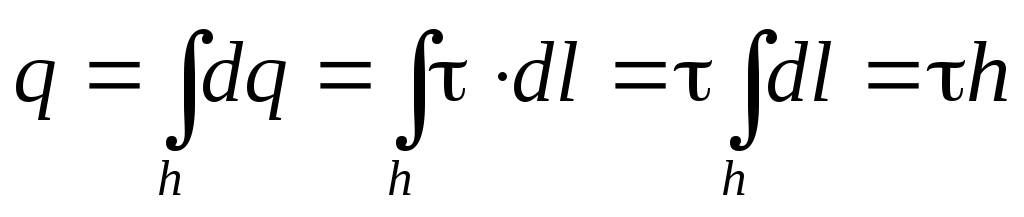
Таким образом
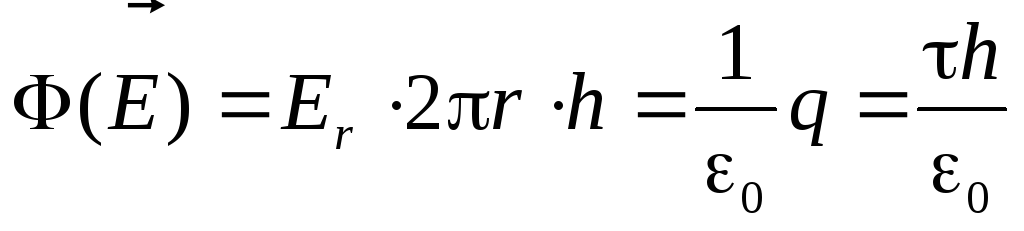 (2.12)
(2.12)
Отсюда теперь легко получить знакомую нам гиперболическую зависимость напряжённости поля от расстояния до нити - r (см. 1.11).
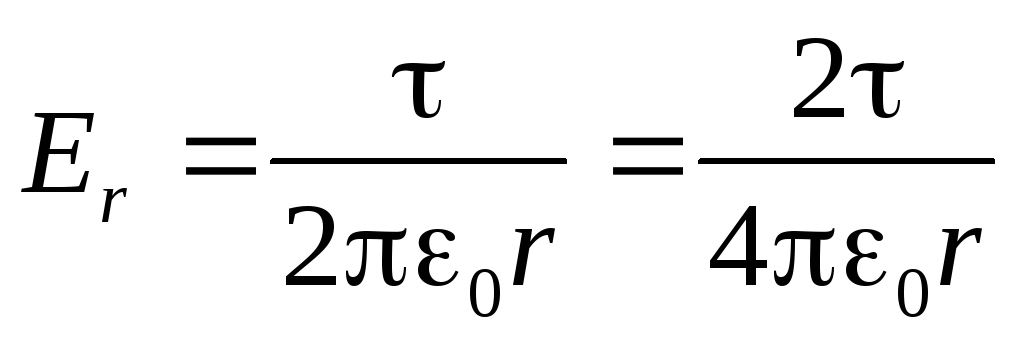 (2.13)
(2.13)
Поле бесконечной равномерно заряженной плоскости. Поле плоского конденсатора
Пусть электрическое поле создаётся зарядом, равномерно распределённым по поверхности безграничной плоскости, с поверхностной плотностью (рис. 2.8.)
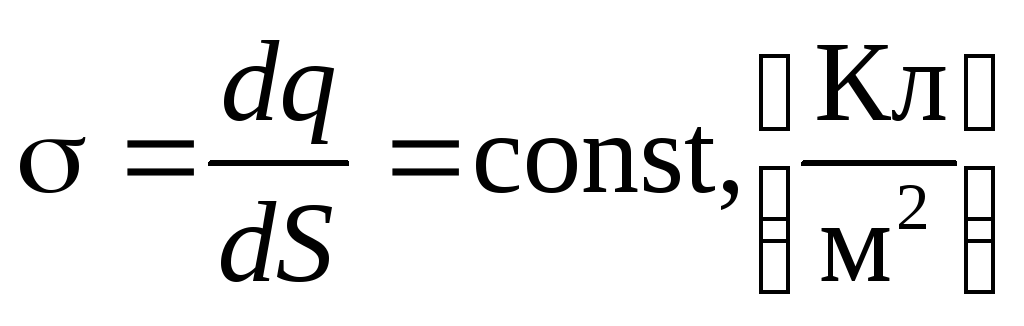
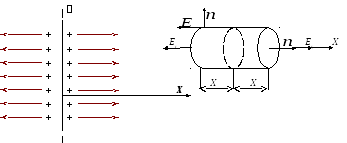
Рис. 2.8.
Из симметрии задачи следует, что поле повсюду направлено перпендикулярно к поверхности. Выясним, как меняется напряжённость поля по мере удаления от заряженной плоскости.
В качестве гауссовой поверхности удобно выбрать цилиндр. Ось цилиндра направим перпендикулярно плоскости, его основание расположим на расстоянии Х симметрично по обе стороны от поверхности.
Вычислим поток вектора напряжённости
через боковую поверхность и основания
цилиндра. Как следует из рис. 2.8., поток
вектора напряжённости
 через боковую поверхность цилиндра
равен нулю, так как здесь повсюду векторы
напряжённости «скользят» по поверхности
и
через боковую поверхность цилиндра
равен нулю, так как здесь повсюду векторы
напряжённости «скользят» по поверхности
и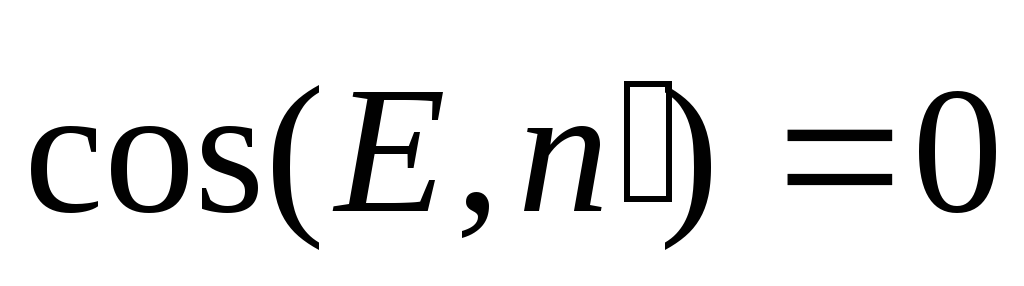 .
.
Тогда полный поток через замкнутую цилиндрическую поверхность можно записать как поток через два основания цилиндра.
Это величина, рассчитанная по определению потока.
Теперь воспользуемся теоремой Гаусса, заметив, что заряд q , «находящийся внутри гауссовой поверхности», в данном случае сосредоточен на площадкеS =S осн, «вырезанной» цилиндром на бесконечной плоскости
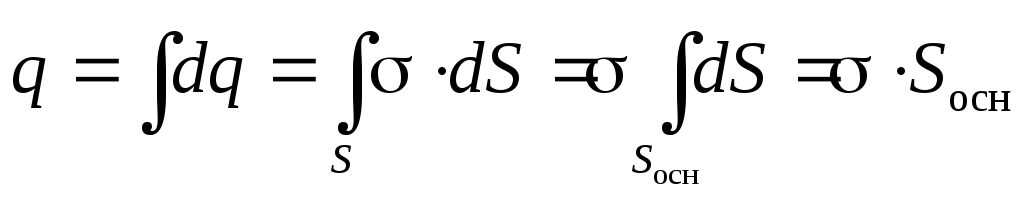 (2.15)
(2.15)
Объединим результаты(2.15) и (2.14) в уравнение Гаусса:
![]()
Откуда следует
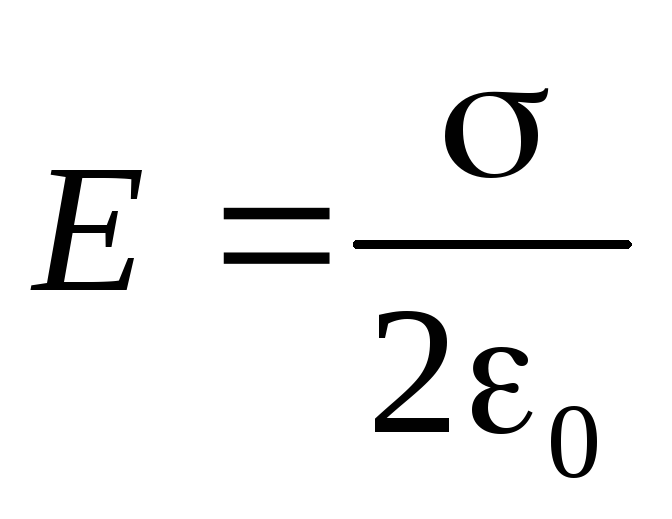 (2.16)
(2.16)
Вывод. Поле, созданное бесконечной равномерно заряженной плоскостью, однородно. Оно не меняется с расстоянием от заряженной поверхности ни по величине, ни по направлению.
Теперь рассмотрим еще один важный пример. Пусть поле создаётся двумя бесконечными плоскостями, заряженными разноименно, но с одинаковой по величине поверхностной плотностью заряда (рис. 2.9.). Это важная идеализация электростатики - плоский конденсатор . Каждая обкладка этого конденсатора создаёт однородное поле, напряжённость которого мы только что установили (2.16):
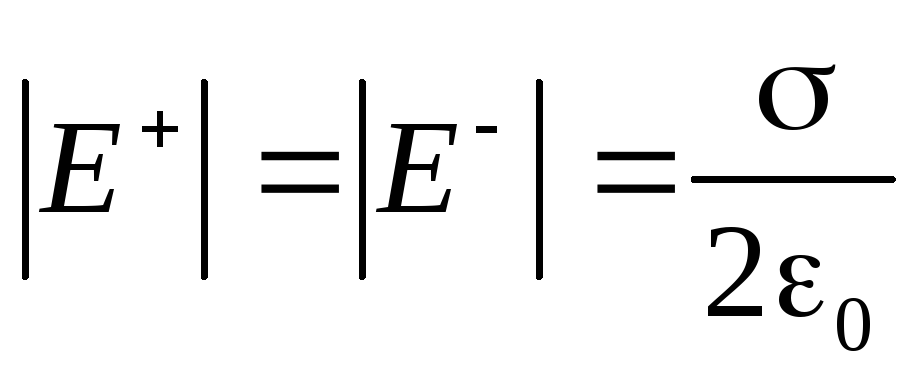 .
.
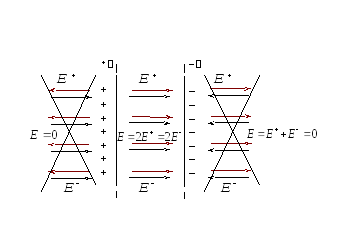
Рис. 2.9.
Силовые линии поля положительно заряженной плоскости направлены от неё, а отрицательной - к плоскости. При сложении этих полей, напряжённость результирующего поля вне конденсатора оказывается равной нулю, а внутри конденсатора, где эти поля совпадают по направлению, - поле удваивается:
![]() . (2.17)
. (2.17)
Пример 1 . Тонкая, бесконечно длинная нить заряжена однородно с линейной плотностью заряда λ . Найти напряженность электростатического поля Е (r ) на произвольном расстоянии r от нити.
Сделаем рисунок:

Анализ:
Т.к. нить несет не точечный заряд, применим метод ДИ. Выделим бесконечно малый элемент длины проводника dl
, который будет содержать заряд dq
=dlλ
. Рассчитаем напряженность поля, созданного каждым элементом проводника в произвольной точке А, находящейся от нити на расстоянии а
. Вектор будет направлен вдоль прямой, соединяющей точечный заряд с точкой наблюдения. Результирующее поле получим по нормали к нити вдоль оси х. Необходимо найти величину dE x
:
dE x
=
dE
cosα
.![]() .
.
По определению:
![]() .
.
Величина dl , r , меняются согласованно при изменении положения элемента dl . Выразим их через величину α:
где dα – бесконечно малое приращение угла α в результате поворота радиуса-вектора относительно точки А при перемещении по нити на dl . Тогда dl= r 2 dα/ а . При перемещении dl от до точки О угол меняется от 0 0 до π/2.
Следовательно ![]() .
.
Проверка размерности:[Е]=В/м=кгм/мфм=КлВ/Клм=В/м;
Ответ:
![]() .
.
Способ 2.
В силу аксиальной симметрии распределения заряда, все точки, расположены на равном расстоянии от нити, эквивалентны и напряженность поля в них одинакова, т. е. Е (r )=const, где r - расстояние от точки наблюдения до нити. Направление Е в этих точках всегда совпадает с направлением нормали к нити. По теореме Гаусса ; где Q -заряд, охваченный поверхностью – S’ через которую вычисляется поток, выберем в виде цилиндра радиусом а и образующей с нитью. Учитывая, что нормален боковой поверхности цилиндра, получим для потока:
Т. к. Е =const.
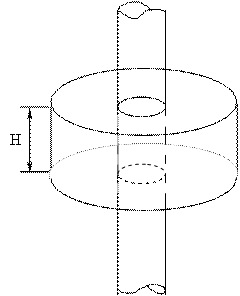
S бок.пов. =На 2π .
С другой стороны Е 2πаН=Q/ε 0 ,
где λН=q .
Ответ: Е =λ /4πε 0 а .
Пример 2 . Рассчитать напряженность равномерно заряженной бесконечной плоскости с поверхностной плотностью зарядов σ .
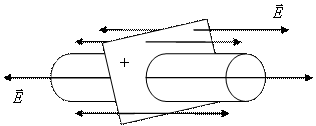
Линии напряженности перпендикулярны и направлены в обе стороны от плоскости. В качестве замкнутой поверхности выберем поверхность цилиндра, основания которого параллельны плоскости, а ось цилиндра перпендикулярна плоскости. Т.к. образующие цилиндра параллельны линиям напряженности (α=0, cos α=1), то поток вектора напряженности сквозь боковую поверхность равна нулю, а полный поток сквозь замкнутую цилиндрическую поверхность равен сумме потоков сквозь его основание. Заряд, заключенный внутри замкнутой поверхности равен σS осн. , тогда:
Ф Е =2Е S осн или Ф Е = = , тогда E = =
Ответ: E =, не зависит от длинны цилиндра и на любых расстояниях от плоскости одинакова по модулю. Поле равномерно заряженной плоскости однородно.
Пример 3 . Рассчитать поле двух бесконечно заряженных плоскостей, с поверхностной плотностью +σ и –σ соответственно.
E = E = 0 ; E = E + + E - = .
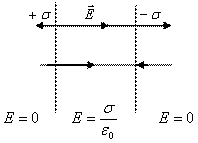
Ответ: Результирующая напряженность поля в области между плоскостями равна E =, а вне объема, ограниченного плоскостями равняется нулю.
Пример 4 . Рассчитать напряженность поля равномерно заряженной с поверхностной плотностью заряда +σ сферической поверхности радиуса R .
То , и ,
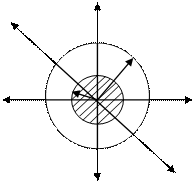
если r < R , то внутри замкнутой поверхности нет зарядов и электростатическое поле отсутствует (Е=0).
Ответ: .
Пример 5 . Рассчитать напряженность объемно заряженной с объемной плотностью ρ , шара радиусам R .
В виде замкнутой поверхности возьмем сферу.
Если r ≥R , то = 4πr 2 E ; E =
если r < R , то сфера радиусом r , охватывает заряд q" равный q"= (так как заряды относятся как объёмы, а объёмы, как кубы радиусов)
Тогда по т.Гаусса
![]()
Ответ: ; внутри равномерно заряженного шара напряжённость растет линейно с расстоянием r от его центра, а вне - убывает обратно пропорционально r 2 .
Пример № 6 . Рассчитать напряжённость поля бесконечного, круглого цилиндра, заряженного с линейной плотностью заряда λ , радиуса R .
Поток вектора напряженности сквозь торцы цилиндра равен 0, а сквозь боковую поверхность:
Т.к. , или ,
тогда ![]() (если r
> R
)
(если r
> R
)
если λ > 0, Е > 0 , вектор Ē направлен от цилиндра,
если λ < 0, Е < 0 , вектор Ē направлен к цилиндру.
Если r < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е = 0
Ответ: (r > R ) ; E = 0 (R >r ). Внутри равномерно заряженного по поверхности бесконечного, круглого цилиндра, поля нет.
Пример 7 . Электрическое поле создано двумя бесконечно длинными параллельными плоскостями с поверхностными плоскостями зарядов 2 нКл/м 2 и 4нКл/м 2 . Определить напряжённость поля в областях І, ІІ, ІІІ. Построить график зависимости Ē (r ) .
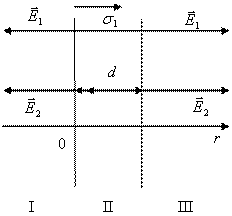
Плоскости делят пространство на 3 области
Направление Ē результирующего поля в сторону большего.
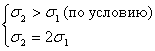
В проекции на r :
; «–»;![]() ;
;
; «–»;![]() ;
;
; «+»;![]() .
.
График Ē (r )
Выбор масштаба: Е 2 =2 Е 1
Е 1 = 1; Е 2 =2
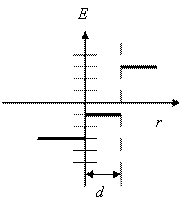
Ответ: Е І = –345 В/м; Е І I = –172 В/м; Е І II = 345 В/м.
Пример № 8 . Эбонитовый сплошной шар радиусом R = 5 см несет заряд, равномерно распределенный с объёмной плотностью ρ =10 нКл/м 3 . Определить напряженность электрического поля в точках: 1) на расстоянии r 1 = 3 см от центра сферы; 2) на поверхности сферы; 3) на расстоянии r 2 = 10 см от центра сферы.
Рассмотрим поле, созданное зарядом, равномерно распределенным по бесконечной нити. Эту задачу мы решили на прошлой лекции, воспользовавшись принципом суперпозиции электрических полей (см. 1.11).
Теперь покажем, несколько проще можно рассчитать это поле с помощью теоремы Гаусса.
Определим напряжённость поля на расстоянии r от нити, заряженной с постоянной линейной плотностью :
, [Кл/м] (2.10)
Окружим нить замкнутой цилиндрической поверхностью (рис. 2.7.). Высота цилиндра - h , а радиус его основания - r .
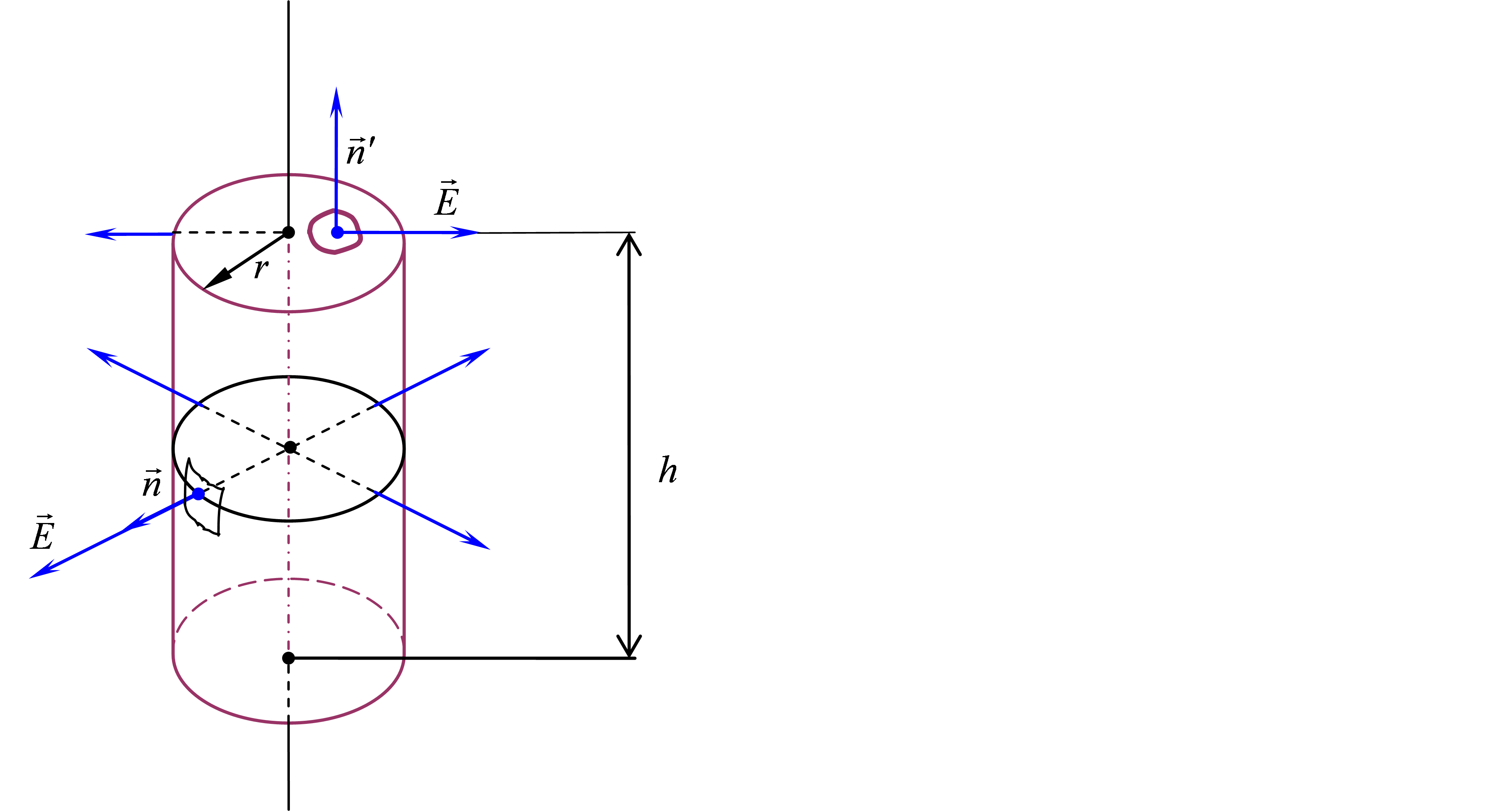
Поле, созданное заряженной нитью, обладает цилиндрической симметрией. В связи с этим векторы напряжённости во всех точках боковой поверхности цилиндра будут одинаковы по модулю и направлены радиально, то есть перпендикулярно к боковой поверхности цилиндра. На основаниях цилиндра векторы , направленные по-прежнему радиально, «скользят» по основанию, образуя прямой угол с нормалью .
Вычислим поток вектора через поверхность выбранного цилиндра. Полный поток через эту замкнутую «гауссову» поверхность складывается из потока через боковую поверхность цилиндра и через два его основания:
Последние два интеграла равны нулю, так как «скользящие» по основаниям цилиндра векторы не пронизывают их и не создают никакого потока. Формально эти два интеграла равны нулю, так как между векторами и прямой угол и . Таким образом
![]()
Во всех точках боковой поверхности цилиндра E =Е r = const и .
Поэтому поток через боковую поверхность цилиндра равен
Это поток вектора напряжённости электрического поля, вычисленный по определению потока.
Теперь воспользуемся теоремой Гаусса, отметив предварительно, что «заряд, заключённый внутри гауссовой поверхности» в данном случае сосредоточен на отрезке нити h - на оси цилиндра:
Таким образом
![]() (2.12)
(2.12)
Отсюда теперь легко получить знакомую нам гиперболическую зависимость напряжённости поля от расстояния до нити - r (см. 1.11).
Поле бесконечной равномерно заряженной плоскости. Поле плоского конденсатора
Пусть электрическое поле создаётся зарядом, равномерно распределённым по поверхности безграничной плоскости, с поверхностной плотностью s (рис. 2.8.)
![]()
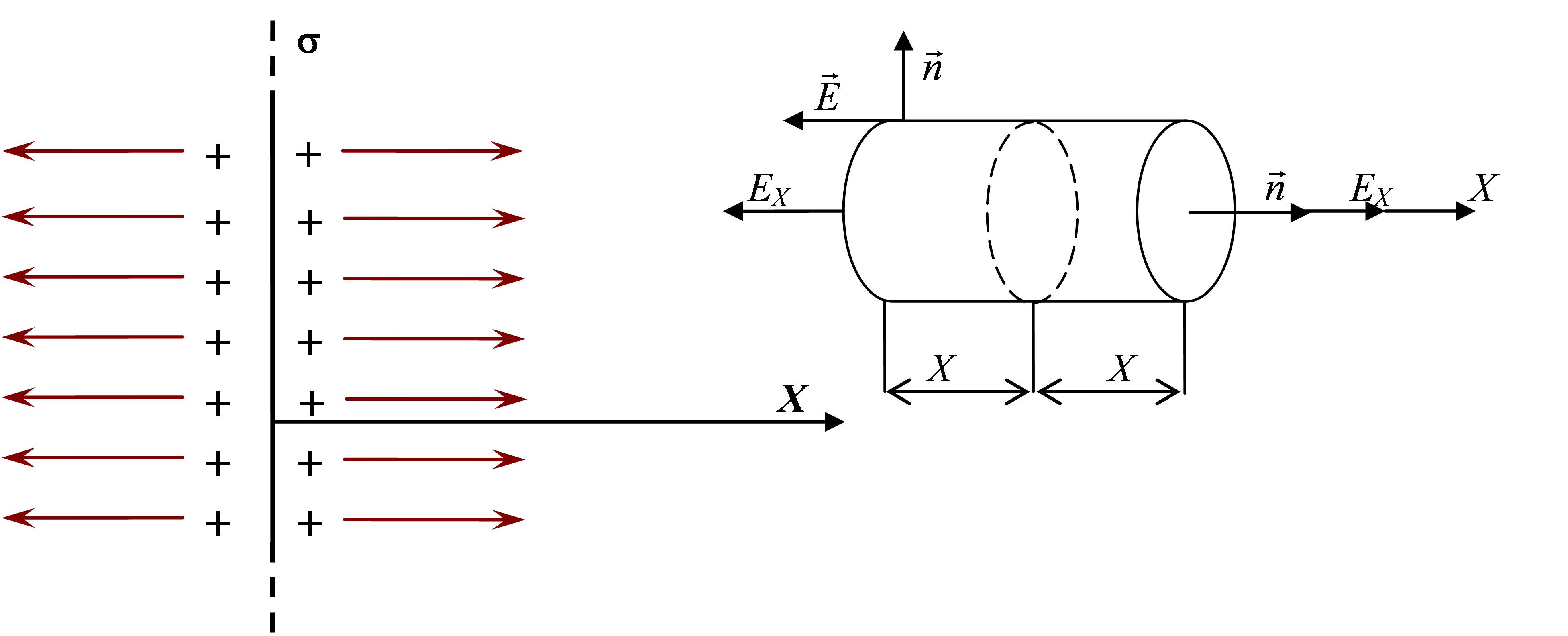
Из симметрии задачи следует, что поле повсюду направлено перпендикулярно к поверхности. Выясним, как меняется напряжённость поля по мере удаления от заряженной плоскости.
В качестве гауссовой поверхности удобно выбрать цилиндр. Ось цилиндра направим перпендикулярно плоскости, его основание расположим на расстоянии Х симметрично по обе стороны от поверхности.
Вычислим поток вектора напряжённости через боковую поверхность и основания цилиндра. Как следует из рис. 2.8., поток вектора напряжённости через боковую поверхность цилиндра равен нулю, так как здесь повсюду векторы напряжённости «скользят» по поверхности и .
Тогда полный поток через замкнутую цилиндрическую поверхность можно записать как поток через два основания цилиндра.
Это величина, рассчитанная по определению потока.
Теперь воспользуемся теоремой Гаусса, заметив, что заряд q , «находящийся внутри гауссовой поверхности», в данном случае сосредоточен на площадке S = S осн, «вырезанной» цилиндром на бесконечной плоскости
Объединим результаты(2.15) и (2.14) в уравнение Гаусса:
![]()
Откуда следует
Вывод. Поле, созданное бесконечной равномерно заряженной плоскостью, однородно. Оно не меняется с расстоянием от заряженной поверхности ни по величине, ни по направлению.
Теперь рассмотрим еще один важный пример. Пусть поле создаётся двумя бесконечными плоскостями, заряженными разноименно, но с одинаковой по величине поверхностной плотностью заряда (рис. 2.9.). Это важная идеализация электростатики - плоский конденсатор . Каждая обкладка этого конденсатора создаёт однородное поле, напряжённость которого мы только что установили (2.16):
![]() .
.
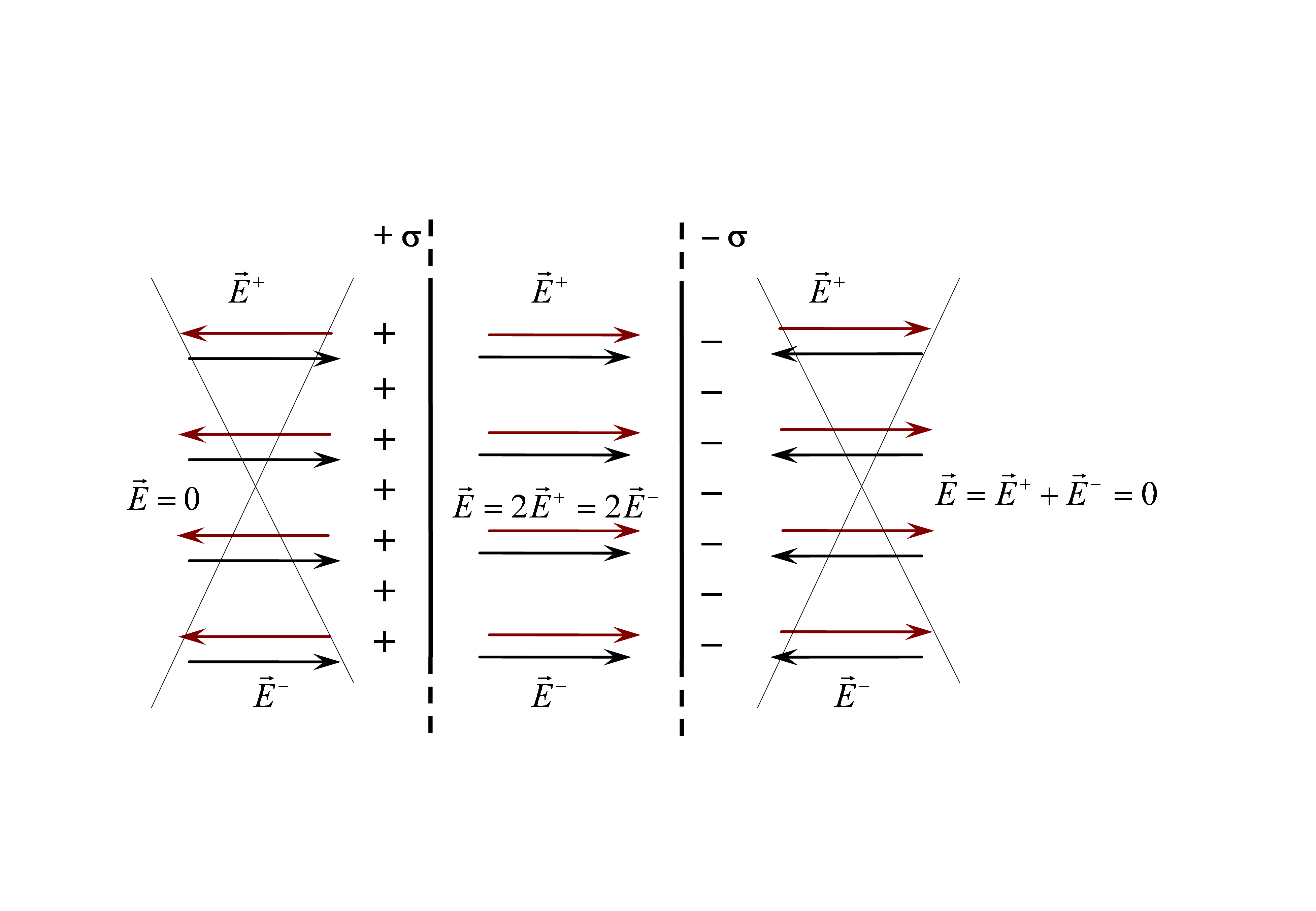
Силовые линии поля положительно заряженной плоскости направлены от неё, а отрицательной - к плоскости. При сложении этих полей, напряжённость результирующего поля вне конденсатора оказывается равной нулю, а внутри конденсатора, где эти поля совпадают по направлению, - поле удваивается.




