Третье уравнение Максвелла является обобщением закона Гаусса на случай переменных процессов. Закон Гаусса связывает поток вектора электрического смещения через произвольную замкнутую поверхность S с зарядом Q, сосредоточенным внутри этой поверхности:

где dS = n0dS ; n0 – орт внешней нормали к поверхности S.

До Максвелла уравнение (1.40) рассматривалось только в применении к постоянным полям. Максвелл предположил, что оно справедливо и в случае переменных полей.

Заряд Q может быть произвольно распределен внутри поверхности S. Поэтому в общем случае

где ρ – объемная плотность зарядов; V - объем, ограниченный поверхностью S. Объемная плотность зарядов

где ΔQ – заряд, сосредоточенный в объеме ΔV. Размерность ρ – кулон на кубический метр (Кл/м3).

Подставляя (1.41) в (1.40), получаем

. (1.43)

Уравнение (1.43) обычно называют третьим уравнением Максвелла в интегральной форме. Для перехода к дифференциальной форме преобразуем левую часть этого уравнения по теореме Остроградского-Гаусса (П. 19). В результате получим:

Это равенство должно выполняться при произвольном объеме V , что возможно только в том случае, если

divD = ρ. (1.44)

Соотношение (1.44) принято называть третьим уравнением Максвелла. В декартовой системе координат оно записывается в виде

Из равенства (1.44) следует, что дивергенция вектора D отлична от нуля в тех точках пространства, где имеются свободные заряды. В этих точках линии вектора D имеют начало (исток) или конец (сток). Линии вектора D начинаются на положительных зарядах и заканчиваются – на отрицательных.

В отличие от вектора D истоками (стоками) вектора Е могут быть как свободные, так и связанные заряды. Чтобы показать это, перепишем уравнение (1.44) для вектора Е. Подставляя соотношение (1.4) в (1.44), получаем εоdiv Е = ρ – div P. Второе слагаемое в правой части этого равенства имеет смысл объемной плотности зарядов , возникающих в результате неравномерной поляризации среды (такие заряды будем называть поляризационными ):

divP = -. (1.45)

Поясним возникновение поляризационных зарядов на следующем примере. Пусть имеется поляризованная среда (рис. 1.8). Выделим мысленно внутри нее объем ΔV, ограниченный поверхностью ΔS. В результате поляризации в среде происходит смещение зарядов, связанных с молекулами вещества. Если объем ΔV мал, а поляризация неравномерная, то в объем ΔV с одной стороны может войти больше зарядов, чем выйдет с другой (на рис. 1.8 объем ΔVпоказан пунктиром). Подчеркнем, что поляризационные заряды являются "связанными" и возникают только под действием электрического поля. Знак минус в формуле (1.45) следует из определения вектора Р (см. 1.2.1).

Рис. 1.8. Поляризованная среда

Линии вектора Р начинаются на отрицательных зарядах и оканчиваются на положительных. С учетом формулы (1.45) приходим к соотношению εоdiv Е = ρ + ρp, из которого и следует сделанное выше утверждение, что истоками (стоками) линий вектора Е (силовых линий электрического поля) являются как свободные, так и связанные заряды.

Четвертое уравнение Максвелла в интегральной форме совпадает с законом Гаусса для магнитного поля, который можно сформулировать следующим образом. Поток вектора В через любую замкнутую поверхность S равен нулю, т.е.

.(1.46)

Это означает, что не существует линий вектора В, которые только входят в замкнутую поверхность S (или, наоборот, только выходят из поверхности S): они всегда пронизывают ее (рис. 1.9).

Рис. 1.9. Линии вектора В, пронизывающие поверхность S

Уравнение (1.46) называют четвертым уравнением Максвелла в интегральной форме. К дифференциальной форме уравнения (1.46) можно перейти с помощью теоремы Остроградского-Гаусса так же, как это было сделано в случае третьего уравнения Максвелла. В результате получим

divB = 0. (1.47)

Уравнение (1.47) представляет собой четвертое уравнение Максвелла. Оно показывает, что в природе отсутствуют уединенные магнитные заряды одного знака. Из этого уравнения также следует, что линии вектора В (силовые линии магнитного поля) являются непрерывными.

В основе теории Максвелла лежат рассмотренные выше четыре уравнения:

1. Электрическое поле может быть как потенциальным (Е Q ), так и вихревым (Е B ), поэтому напряженность суммарного поля Е =Е Q +Е B . Так как циркуляция вектора Е Q равна нулю (см. (137.3)), а циркуляция вектора Е B определяется выражением (137.2), то циркуляция вектора напряженности суммарного поля

Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):

Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.

3. Теорема Гаусса для поля D (см. (89.3)):

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, то формула (139.1) запишется в виде

4. Теорема Гаусса для поля В (см. (120.3)):

Итак, полная система уравнений Максвелла в интегральной форме:

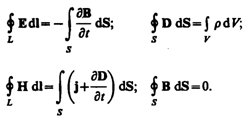
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):

где e 0 и m 0 - соответственно электрическая и магнитная постоянные, e и m - соответственно диэлектрическая и магнитная проницаемости, g - удельная проводимость вещества.

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.

Для стационарных полей (E= const и B= const) уравнения Максвелла примут вид

т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного - только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.

Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса

можно представить полную систему уравнении Максвелла в дифференциальном форме (характеризующих поле в каждой точке пространства):

Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла - интегральная и дифференциальная - эквивалентны. Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.

Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше:

(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).

Уравнения Максвелла - наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т. е. электрическое и магнитное поля неразрывно связаны друг с другом - они образуют единое электромагнитное поле .

Ток смещения или абсорбционный ток - величина, прямо пропорциональная быстроте изменения электрической индукции. Это понятие используется вклассической электродинамике

Введено Дж. К. Максвеллом при построении теории электромагнитного поля.

Введение тока смещения позволило устранить противоречие в формуле Ампера для циркуляции магнитного поля, которая после добавления туда тока смещения стала непротиворечивой и составила последнее уравнение, позволившее корректно замкнуть систему уравнений (классической) электродинамики.

Строго говоря, ток смещения не является электрическим током, но измеряется в тех же единицах, что и электрический ток.

ного коэффициента) называется поток вектора быстроты изменения электрического поля через некоторую поверхность :

(СИ)

ВВЕДЕНИЕ В ЭЛЕКТРОРАЗВЕДКУ

Учебно-методическое пособие для слушателей курсов повышения квалификации специальности «Геофизика» по программе «Методы поисков и разведки месторождений полезных ископаемых в промысловой и разведочной геофизике»

Казань 2009

Печатается по решению Редакционно-издательского совета ГОУ ВПО «Казанский государственный университет им. В.И. Ульянова–Ленина»

Утверждено на заседании кафедры геофизики

Казанского государственного университета,

Протокол №____от____ ______________2009

Д.И. Хасанов

Введение в электроразведку: пособие для самостоятельного изучения для слушателей курсов повышения квалификации специальности «Геофизика». – Казань: Казанский государственный университет, 2009. - 75 с.

Настоящее учебно-методическое пособие предназначено для слушателей курсов повышения квалификации специальности «Геофизика» по программе «Методы поисков и разведки месторождений полезных ископаемых в промысловой и разведочной геофизике». В пособии рассмотрены наиболее общие вопросы электроразведки. Приведены примеры использования электроразведочных данных для решения различных геологических задач.

университет, 2009

Введение

Глава 1. Теоретические основы электроразведки________________________ 4

Глава 2. Естественные электрические поля _____________________________8

Глава 3. Искусственные электрические поля ___________________________22

Глава 4. Методы профилирования ____________________________________30

Глава 5. Методы электромагнитного зондирования _____________________49

Глава 6. Электромагнитные свойства горных пород _____________________69

Литература__________________________________________________________74

Контрольные вопросы________________________________________________75

Введение

Электрическая разведка или просто электроразведка - это большая группа геофизических методов изучающих электромагнитные поля различной природы. Целью этих исследований является определение электромагнитных характеристик геологической среды (сопротивление, проводимость, поляризуемость и т.д.), зная которые можно получить ценную информацию о строении изучаемого участка или района. По виду электромагнитных полей электроразведку можно разделить на два отдела: первый - объединяет методы, исследующие естественные, второй – искусственные электромагнитные поля.

Глава 1. Теоретические основы электроразведки

Уравнения Максвелла

Теория электроразведки базируется на системе уравнений электродинамики - уравнениях Максвелла [Жданов, 1986]. Эти уравнения для любой точки пространства вне сторонних источников поля записываются в виде:

Здесь и - векторы напряженности электрического и магнитного полей, и - векторы электрической и магнитной индукции, - вектор плотности тока проводимости, - плотность электрических зарядов.

Уравнения Максвелла дополняются уравнениями связи:

где , и - электромагнитные свойства среды: электропроводность, диэлектрическая и магнитная проницаемости. Отметим, что первое уравнение связи представляет собой закон Ома в дифференциальной форме.

Физический смысл уравнений Максвелла

Первое уравнение Максвелла представляет собой дифференциальное выражение закона полного тока, согласно которому циркуляция магнитного поля по замкнутому контуру равна полному току в нем. Оно указывает, что магнитное поле порождается как токами проводимости (первое слагаемое в правой части уравнения), так и токами смещения (второе слагаемое). Причем токи проводимости - это движение зарядов, а токи смещения - скорость изменения электрической индукции.

Второе уравнение есть дифференциальное выражение закона электромагнитной индукции, согласно которому изменение магнитной индукции возбуждает вихревое электрическое поле. Таким образом, переменное магнитное поле порождает переменное электрическое, постоянное же магнитное поле не создает поля электрического.

Третье уравнение указывает, что в природе магнитных зарядов не существует, и силовые линии поля магнитной индукции замкнуты.

Четвертое уравнение говорит, что источниками поля электрической индукции являются электрические заряды. Изолинии поля электрической индукции начинаются на этих зарядах и непрерывны вне их.

ТЕМА 4.1. Оптика

4.1.1. Теория распространения
электромагнитных волн Максвелла.
Уравнения Максвелла

Теория Д.К. Максвелла лежит в основе объяснения существования и свойств любых электромагнитных волн, таких, как световые волны, радиоволны, инфракрасное и ультрафиолетовое излучения. Эта теория является феноменологической, т.е. в ней не рассматриваются молекулярное строение среды и внутренний механизм процессов, происходящих в среде под действием электрического и магнитного полей. Электрические и магнитные свойства среды характеризуются относительной диэлектрической проницаемостью ε, относительной магнитной проницаемостью m и удельной электрической проводимостью σ. Предполагается, что эти параметры среды определяются из эксперимента.

Теория Максвелла - макроскопическая. Это означает, что рассматриваются макроскопические поля зарядов и токов, пространственные размеры которых неизмеримо больше размеров отдельных молекул и атомов.

Математическим выражением теории Максвелла служит система из четырех уравнений, которые записывают в двух формах - дифференциальной и интегральной.

Дифференциальные уравнения Максвелла получаются из интегральных с помощью двух теорем векторного анализа: теоремы Остроградского-Гаусса и теоремы Стокса.

Рассмотрим теорему Остроградского-Гаусса .

Пусть для характеристики какого-либо поля выбран вектор . Тогда поток вектора через произвольную замкнутую поверхность S, мысленно проведенную в этом поле, равен интегралу от дивергенции вектора , взятому по объему V, ограниченному замкнутой поверхностью S:

Операция дивергенции над произвольным вектором сводится к пространственной производной вида:

где a x , a y , a z - проекции вектора на оси прямоугольной декартовой системы координат.

Рассмотрим теорему Стокса .

Пусть для характеристики какого-либо поля выбран вектор . Тогда циркуляция вектора вдоль произвольного замкнутого контура L, мысленно проведенного в этом поле, равна потоку вектора rot через поверхность S, ограниченную замкнутым контуром L:

Векторная операция rot в декартовых координатах выражается так:

Первое уравнение Максвелла

Это уравнение представляет собой обобщение закона электромагнитной индукции Фарадея:

Однако для произвольного контура выполняется взаимосвязь:

Поскольку в общем случае , то для не изменяющегося во времени контура имеет место соотношение:

Сравнивая (4.1.5) и (4.1.7) с учетом (4.1.6), для произвольного контура L, мысленно проведенного в переменном магнитном поле, можно записать:

Силу тока проводимости можно также представить в виде:

или, окончательно:

Из двух последних уравнений (4.1.47) следует, что , что указывает на поперечность электромагнитной волны. Из первого уравнения (4.1.47) ясно, что вектор Н как результат векторного произведения, должен быть перпендикулярен плоскости, в которой лежат вектора и . Аналогично, из второго уравнения (4.1.47) следует, что вектор электрического поля должен быть перпендикулярен плоскости, в которой лежат вектора и . Окончательно получается, что для любой электромагнитной волны вектора , и составляют тройку ортогональных векторов (Рис. 4.1.1).

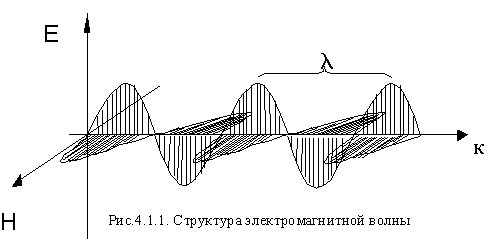
4.1.3. Шкала электромагнитных волн

В зависимости от частоты ν = ω/2π или длины волны в вакууме λ 0 = с/ν, а также способа излучения и регистрации различают несколько видов электромагнитных волн:

радиоволны;
оптическое излучение;
рентгеновское излучение;
гамма-излучение.

Радиволнами называются электромагнитные волны, у которых длина волны в вакууме λ 0 > 5·10 -5 м (ν < 6·10 12 Гц). Весь диапазон радиоволн принято делить на 9 поддиапазонов (Табл. 4.1.1).

Таблица 4.1.1

Оптическим излучением или светом называются электромагнитные волны, у которых длина волны в вакууме лежит в диапазоне 10 нм >λ 0 > 1 мм (границы условны). К оптическому излучению относят инфракрасное, видимое и ультрафиолетовое излучения.

Инфракрасным (ИК) называются электромагнитные волны, испускаемые нагретыми телами, у которых длина волны в вакууме лежит в диапазоне 1 мм > λ 0 > 770 нм.

Видимым излучением (светом) называются электромагнитные волны, у которых длины волны в вакууме лежат в диапазоне 770 нм > λ 0 > 380 нм. Свет способен вызывать зрительные ощущения в человеческом глазе.

Ультрафиолетовым излучением (УФ) называются электромагнитные волны, у которых длины волны в вакууме лежат в диапазоне 380 нм > λ 0 > 10 нм.

Рентгеновским излучением (рентгеновскими лучами) называются электромагнитные волны, которые возникают при взаимодействии заряженных частиц и фотонов с атомами вещества. Оно характеризуется длинами волны в вакууме в диапазоне с условными границами (10-100 нм) > λ 0 > (0,01-1 пм).

Гамма-излучением (γ-лучами) называются электромагнитные волны с длинами волны в вакууме 0,1 нм > λ 0 . Это излучение испускается возбужденными атомными ядрами при радиоактивных превращениях и ядерных реакциях, а также возникает при распаде частиц, аннигиляции пар "частица-античастица" и других процессах.

4.1.4. Световая волна

Свет представляет собой сложное явление: в одних случаях он ведет себя как электромагнитная волна, в других - как поток особых частиц (фотонов).

В электромагнитной волне колеблются векторы электрического и магнитного полей. Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются наличием колебаний электрического вектора, который называют в этом случае световым вектором . Его изменения в пространстве и времени задаются уравнением плоской волны:

Здесь r - расстояние, отсчитываемое вдоль направления распространения волны.

Отношение скорости световой волны в вакууме с к ее фазовой скорости v в некоторой прозрачной среде называется абсолютным показателем преломления этой среды:

Показатель преломления связан с относительными диэлектрической и магнитной проницаемостями соотношением:

Для подавляющего большинства прозрачных веществ величина μ ≈ 1. Поэтому можно считать, что выполняется:

Значения показателя преломления характеризуют оптическую плотность среды. Среда с большим n будет более оптически плотной.

Длины волн видимого света в вакууме заключены в пределах:

В веществе длины волн будут другими. В случае колебаний с частотой ν длина волны света в вакууме равна:

Используя соотношение (4.1.49), имеем для длины света в веществе формулу:

Частоты видимого света лежат в пределах:

Модуль среднего по времени потока энергии, переносимого волной, называется интенсивностью света I в данной точке пространства. Интенсивность пропорциональна квадрату амплитуды волны:

I ∼ A 2

(4.1.56)

Световая волна, как и другие электромагнитные волны, является поперечной, т.е. направления колебаний электрического и магнитного векторов перпендикулярны к направлению ее распространения. В естественном свете присутствуют все направления колебаний электрического и магнитного векторов. Если в волне присутствуют колебания электрического вектора только в одной плоскости (а магнитного вектора в перпендикулярной плоскости), такую волну называют плоскополяризованной (линейно поляризованной) . Есть и более сложные случаи поляризации волн - круговая и эллиптическая. В случае круговой поляризации электрический и магнитный векторы вращаются по кругу с частотой изменения волны.

4.1.5. Геометрическая оптика

Длины воспринимаемых глазом световых волн очень малы (∼10 -7 м), поэтому распространение видимого света в первом приближении можно рассматривать, отвлекаясь от его волновой природы и полагая, что свет распространяется вдоль некоторых прямых линий, называемых лучами. В предельном случае, когда длина волны света λ→0, законы оптики можно сформулировать на языке геометрии.

Основу геометрической оптики составляют 4 закона:

закон прямолинейного распространения света;
закон независимости световых лучей;
закон отражения света;
закон преломления света.

Закон прямолинейного распространения света утверждает, что в однородной среде свет распространяется прямолинейно . Этот закон является приближенным: при прохождении света через очень малые отверстия, размеры которых сравнимы с диной волны света, наблюдается отклонение от прямолинейности, тем большее, чем меньше отверстие.

Закон независимости световых лучей утверждает, что лучи при пересечении не возмущают друг друга . Это означает, что пересечение лучей не мешает каждому из них распространяться независимо друг от друга. Этот закон справедлив при не слишком больших интенсивностях световых волн.

В основу геометрической оптики был положен принцип Ферма : свет распространяется по такому пути, для прохождения которого ему требуется минимальное время .

Пусть для прохождения участка ds свету требуется время dt = ds/v, где v - скорость света в данной точке среды. Поскольку v = c/n, то получим:

Следовательно, время τ, необходимое для прохождения пути от точки 1 до точки 2 (Рис. 4.1.2), равно:

Рис. 4.1.2. К принципу Ферма

Имеющая размерность длины величина

называется оптической длиной пути . В однородной среде оптическая длина пути равна произведению геометрической длины пути на показатель преломления:

Следовательно,

Пропорциональность времени прохождения оптической длине пути дает возможность сформулировать принцип Ферма так: свет распространяется по такому пути, оптическая длина которого минимальна.

Из принципа Ферма вытекает обратимость световых лучей. Действительно, оптический путь, который минимален при движении света из точки 1 в точку 2, окажется минимальным и в случае распространения света в обратном направлении.

Получим с помощью принципа Ферма законы отражения и преломления света. Пусть свет попадает из точки А в точку В, отразившись от поверхности MN (Рис. 4.1.3).

Рис. 4.1.3. Закон отражения света как следствие принципа Ферма

Прямой путь из А в В прегражден экраном Э. Среда, в которой распространяется луч, однородна, поэтому минимальность оптической длины пути сводится к минимальности геометрической длины пути. Геометрическая длина произвольно взятого пути равна АО"B = A"O"B, поскольку вспомогательная точка A" является зеркальным отражением точки А, и АО" = A"O". Из Рис. 4.1.3 видно, что наименьшей длиной обладает путь луча, отразившегося в точке О, для которой угол отражения равен углу падения. При удалении точки O" от точки О геометрическая длина пути неограниченно возрастает, что противоречит принципу Ферма. Этот результат можно записать так:

Соотношение (4.1.62) выражает закон отражения света : отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; угол отражения равен углу падения.

Найдем точку, в которой должен преломиться луч, распространяясь от А к В, чтобы оптическая длина пути была минимальной (Рис. 4.1.4).

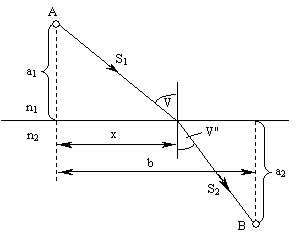
Рис. 4.1.4. К расчету закона преломления света из принципа Ферма

Для произвольного луча оптическая длина пути равна:

Чтобы найти минимальное значение оптической длины пути, продифференцируем L по х и приравняем производную к нулю:

Множители при n 1 и n 2 равны, соответственно, sinθ и sinθ". Поэтому получаем соотношение:

которое выражает закон преломления света. Используя взаимосвязь показателей преломления с фазовыми скоростями распространения света в средах, можно записать соотношение (4.1.65) в виде:

Следовательно, закон преломления света гласит: преломленный луч лежит в одной плоскости с падающим лучом и нормалью; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных веществ.

В (4.1.66) n 12 - относительный показатель преломления второго вещества по отношению к первому. Из (4.1.65) видно, что при переходе света из оптически более плотной среды в оптически менее плотную луч удаляется от нормали к поверхности раздела сред. Увеличение угла падения сопровождается более быстрым ростом угла преломления, и при достижении некоторого предельного угла падения угол преломления будет равным 90°:

При углах падения, лежащих в пределах от θ пред пред до 90°, преломленной волны не существует, вся энергия падающей волны переходит в энергию отраженной волны. Это явление называется полным внутренним отражением.

Таблица 4.1.2

Во многих оптических приборах для преломления света используются стеклянные призмы. На Рис. 4.1.5 показан ход луча монохроматического света в призме.

Рис. 4.1.5. Ход лучей в призме

После двукратного преломления луч оказывается отклоненным от первоначального положения на угол δ (угол отклонения ). Угол θ, заключенный между преломляющими гранями, называется преломляющим углом . Угол δ зависит от преломляющего угла θ и показателя преломления призмы. Эта зависимость может быть легко показана для призмы с малым преломляющим углом θ (тонкой призмы) в случае малого угла падения α. Исходя из закона преломления и принимая значение показателя преломления воздуха равным единице, можно записать:

При малых углах α и θ углы α 1 , γ и γ 1 также малы. Поэтому вместо (4.1.69) можно приближенно записать:

Из четырехугольника BQDE, в котором углы при В и D - прямые, найдем, что угол BED равен 180° - θ. Тогда из четырехугольника BСDE находим:

Угол δ из треугольника BED равен:

Подставляя в (4.1.72) результаты (4.1.73) и (4.1.70), получим окончательно:

4.1.6. Преломление в линзе

В практических применениях большое значение имеет преломление света на сферической границе раздела двух сред. Основная деталь оптических приборов - линза - обычно представляет собой стеклянное тело, ограниченное с двух сторон сферическими поверхностями. В частном случае одна из поверхностей линзы может быть плоской. Такую поверхность можно рассматривать как сферическую с бесконечно большим радиусом кривизны.

Линзы могут быть изготовлены не только из стекла, а из любого прозрачного вещества с показателем преломления, превышающим единицу, например, из кварца, каменной соли, пластмасс и других материалов. Поверхности линз могут быть и более сложной формы - цилиндрические, параболические и т.д.

Рассмотрим линзу, ограниченную двумя сферическими преломляющими поверхностями PO 1 Q и PO 2 Q (Рис. 4.1.6).

Рис. 4.1.6. Тонкая линза

Центр первой преломляющей поверхности PO 1 Q лежит в точке С 1 , центр второй поверхности PO 2 Q - в точке С 2 . Будем считать, что расстояние O 1 O 2 мало по сравнению с O 1 С 1 или O 2 С 2 . В таком случае точки O 1 и O 2 можно считать практически совпадающими с точкой О - оптического центра линзы. Всякая прямая, проходящая через оптический центр, называется оптической осью линзы. Та из осей, которая проходит через центры обеих преломляющих поверхностей, называется главной оптической осью , остальные - побочными осями .

Луч, идущий по какой-либо оптической оси, проходя через тонкую линзу, не меняет своего направления. Лучи, идущие параллельно главной оптической оси, после преломления в линзе пересекаются в одной точке F, расположенной на главной оптической оси и называемой главным фокусом .

Покажем, что лучи, исходящие под небольшими углами α из некоторой точки А, лежащей на главной оптической оси, собираются линзой в одну точку А 1 , расположенную также на этой оптической оси и называемую изображением точки А (Рис. 4.1.7).

Рис. 4.1.7. Преломление в тонкой линзе

Построим плоскости, касательные к поверхностям линзы в точках М и N (в местах падения луча на линзу и его выхода из линзы), и проведем в эти точки радиусы R 1 и R 2 кривизны поверхностей линзы. Тогда луч AMNA 1 можно рассматривать как луч, преломленный в тонкой призме с преломляющим углом θ. Учитывая малость углов α, β, α 1 , β 1 и толщины линзы, можно записать:

где а и b - расстояния от источника света А и от его изображения А 1 до оптического центра линзы.

Из треугольников АНА 1 и ВЕВ 1 следует, что:

Принимая во внимание формулы (4.1.75), получим:

Учтено, что для тонкой линзы h 1 ≈ h 2 ≈ h. Поскольку, согласно формуле () для тонкой призмы выполняется: θ = (n-1)δ, то, с помощью (4.1.77) имеем формулу линзы :

В эту формулу не входит величина h, что означает, что расстояние b не зависит от от положения точки М. Следовательно, все лучи, исходящие из точки А, соберутся после преломления разными частями линзы в одной точке А 1 .

Если точка А находится бесконечно далеко от линзы (а = ∞), т.е. если лучи падают на линзу параллельно главной оптической оси, то, согласно формуле (4.1.78), имеем:

Величина b = f называется фокусным расстоянием линзы :

Фокусом линзы называется точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оптической оси.

Принимая во внимание (4.1.80), формулу линзы (4.1.78) можно сейчас переписать так:

Величина, обратная фокусному расстоянию, называется оптической силой линзы :

Оптическая сила выражается в диоптриях (дп). 1 дп - оптическая сила линзы с фокусным расстоянием в 1 м.

4.1.7. Принцип Гюйгенса

В приближении геометрической оптики свет за преградой не должен проникать в область геометрической тени. В действительности световая волна распространяется во всем пространстве за преградой, проникая проникать в область геометрической тени, причем это проникновение будет тем более существенным, чем меньше размеры отверстия. При диаметре отверстия или ширине щели, сравнимых с длиной волны, приближение геометрической оптики становится совершенно неприменимым.

Качественно поведение света за преградой с отверстием может быть объяснено с помощью принципа Гюйгенса . Согласно принципу Гюйгенса каждая точка, до которой доходит волновое движение, служит центром вторичных волн; огибающая этих волн дает положение фронта волны в следующий момент времени. Пусть на плоскую преграду с отверстием падает параллельный ей фронт волны (Рис. 4.1.8).

Рис. 4.1.8. К принципу Гюйгенса

Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит центром вторичных волн, которые в однородной и изотропной среде будут сферическими. Построив огибающую вторичных волн, можно убедиться в том, что за отверстием волна проникает в область геометрической тени, огибая края преграды.

4.1.8. Интерференция световых волн

Если в среде распространяются одновременно несколько электромагнитных волн, то волны просто накладываются друг на друга, не возмущая одна другую. Это утверждение, подкрепленное опытом, называется принципом суперпозиции.

В случае, когда колебания электрического и магнитного векторов в каждой из волн происходят так, что между соответственными векторами в разных волнах имеется постоянный во времени и в пространстве фазовый сдвиг, такие волны называются когерентными . Очевидно, что условие когерентности может существовать лишь для волн, которые имеют одинаковые частоты и, соответственно, длины волны.

При сложении когерентных волн возникает явление интерференции , заключающееся в том, что электромагнитные волны в одних точках пространства усиливают, а в других ослабляют друг друга.

Пусть две волны одинаковой частоты, распространяющиеся в одном направлении, возбуждают в некоторой точке пространства колебания:

Эти векторы можно представить как вращающиеся с частотой ω вокруг общего начала коор-динат. Поскольку сдвиг фаз различен, в какой-либо момент времени эти вектора займут различные положения (Рис. 4.1.9).

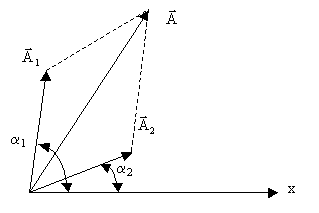
Рис. 4.1.9. К расчету интерференции волн

Используя теорему косинусов, получим амплитуду результирующего колебания:

Если сдвиг фаз между когерентными колебаниями равен нулю (волны - в фазе), то амплитуда результирующей волны максимальна и равна A = A 1 + A 2 . Пусть амплитуды этих волн равны. В этом случае имеем амплитуду результирующей волны:

Если сдвиг фаз между когерентными колебаниями равен ±π (волны - в противофазе), то амплитуда результирующей волны минимальна и равна A = A 1 - A 2 . Если амплитуды этих волн равны, то в этом случае они гасят друг друга:

Когерентные световые волны можно получить, разделив, например, с помощью зеркал волну, излучаемую одним источником, на две. Если заставить эти волны пройти разные пути, а затем наложить их друг на друга, будет наблюдаться интерференция. Пусть такое разделение происходит в точке О (Рис. 4.1.10).

Рис. 4.1.10. Образование когерентных волн

До точки Р первая волна пройдет в среде с показателем преломления n 1 путь S 1 , вторая волна пройдет в среде с показателем преломления n 2 путь S 2 . Если в точке О фаза колебания была равна ωt, то первая волна возбудит в точке Р колебание

а вторая волна - колебание

то разность фаз оказывается кратной 2π, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в фазе. Следовательно, (4.1.93) является условием интерференционного максимума.

Если Δ равна полуцелому числу длин волн в вакууме:

то разность фаз оказывается равной δ = ±(2m + 1)π, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в противофазе. Следовательно, (4.1.94) является условием интерференционного минимума.

4.1.9. Дифракция световых волн

Дифракцией называется совокупность явлений, связанных с отклонениями от законов геометрической оптики. В частности, вследствие дифракции происходит огибание световыми волнами препятствий и проникновение света в область геометрической тени.

Между интерференцией и дифракцией нет существенного физического различия.

Свет, идущий от небольшого яркого источника через круглое отверстие (Рис. 4.1.11) должен по правилам геометрической оптики дать на экране резко ограниченный светлый кружок на темном фоне.

Рис. 4.1.11. Дифракция от круглого отверстия

Такая картина наблюдается при обычных условиях опыта. Но если расстояние от отверстия до экрана в несколько тысяч раз превосходит размеры отверстия, то образуется более сложная картина, которая состоит из совокупности светлых и темных концентрических колец.

Интересный случай дифракции осуществляется с помощью дифракционной решетки, которая представляет собой пластинку, на поверхности которой чередуются узкие параллельные прозрачные и непрозрачные полоски. Сумму ширины прозрачной и непрозрачной полосок называют периодом решетки. Пусть на решетку падает монохроматический свет с длиной волны λ (Рис. 4.1.12). Фронт волны параллелен плоскости решетки.

Рис. 4.1.12. Дифракционная решетка

Разности хода лучей, идущих от соответствующих точек отверстий, например от правых краев (точки А, А 1 , А 2 , ...), или от левых краев (точки В, В 1 , В 2 , ...) имеют одно и то же значение:

Для того, чтобы все пучки усиливали друг друга, необходимо, чтобы разность хода равнялась целому числу длин волн:

где m - целое число.

Это условие позволяет определить те значения углов φ и соответствующие направления, в которых будут наблюдаться максимумы света длины волны λ.

Для данной длины волны может наблюдаться несколько максимумов. Направление, соответствующее m = 0, есть φ = 0. Это - направление первоначального пучка. Соответствущий максимум носит название максимума нулевого порядка. При m = 1 имеем: sinφ 1 = λ/d, при m = 1 имеем: sinφ" 1 = λ/d, т.е. имеется два максимума первого порядка, расположенных симметрично по обеим сторонам от нулевого максимума. Аналогично располагаются максимумы второго, третьего и т.д. порядков.

Отсюда следует, что для волн разной длины λ положения максимумов нулевого порядка совпадают , а положения максимумов первого, второго и т.д. порядков различны: чем больше λ, тем больше соответствующие углы.

Если на решетку падает белый свет, то в плоскости экрана получается ряд цветных изображений щели. На месте нулевого максимума будет изображение щели в белом свете, а по обе стороны от него развернутся цветные полосы от фиолетового к красному концу.

Чем больше общий размер решетки, т.е. чем больше полосок она содержит, тем выше ее качество: увеличение числа полосок увеличивает количество пропускаемого решеткой света (максимумы становятся ярче), и улучшает разрешение близких волн (максимумы становятся резче).

Зная период дифракционной решетки, ее можно использовать для определения длины световой волны, измерив величину угла φ, определяющего положение максимума данного порядка. В этом случае имеем:

Измерение длины световой волны с помощью дифракционной решетки принадлежит к числу наиболее точных методов.

4.1.10. Поляризация световых волн

Поляризованным называется свет, в котором направления колебаний электрического и магнитного векторов упорядочены каким-либо образом. В естественном свете колебания происходят в различных направлениях, быстро и беспорядочно сменяя друг друга.

Различают свет эллиптически поляризованный, поляризованный по кругу, плоскополяризованный. В случае эллиптической или круговой поляризаций электрический и магнитный векторы вращаются в пространстве с частотой, равной частоте волны, причем концы этих векторов описывают либо эллипс, либо круг. Вращение может происходить как по, так и против часовой стрелки. Если вектор вращается в пространстве как правый винт, то поляризацию называют правой, и левой - если вектор вращается в пространстве как левый винт.

Важный частный случай - плоская поляризация. В этом случае вектор электрического поля колеблется в плоскости, проходящей через направление распространения волны и этот вектор. Такую плоскость называют плоскостью колебаний . Вектор магнитного поля колеблется в плоскости, также проходящей через направление распространения волны и этот вектор, но данная плоскость - плоскость поляризации - составляет с плоскостью колебаний прямой угол (Рис. 4.1.13).

Рис. 4.1.13. Структура плоскополяризованной световой волны

Плоскополяризованный свет можно получить из естественного с помощью устройств, которые называются поляризаторами . Эти устройства свободно пропускают волны с колебаниями, плоскость которых совпадает с плоскостью пропускания поляризатора, и задерживают все другие волны.

Пусть на поляризатор падает плоскополяризованный свет амплитуды А 0 и интенсивности I 0 . Сквозь устройство пройдет составляющая колебания с амплитудой А || = А 0 cosφ, где угол φ - угол между плоскостью колебаний падающего света и плоскостью пропускания поляризатора (Рис. 4.1.14).

Рис. 4.1.14. Прохождение плоскополяризованного света через поляризатор

Следовательно, интенсивность прошедшего света определяется выражением:

Это соотношение носит название закона Малюса.

Пусть на пути естественного луча стоят два поляризатора, плоскости пропускания которых составляют угол φ. Из первого поляризатора выйдет плоскополяризованный свет, интенсивность которого I0 составит половину интенсивности естественного неполяризованного света I ест. Используя закон Малюса, получаем:

Максимальная интенсивность получается при φ = 0 (плоскости пропускания поляризаторов параллельны). При φ = 90° интенсивность равна нулю - скрещенные поляризаторы не пропускают свет.

4.1.11. Вращение плоскости
поляризации световых волн

Некоторые вещества, называемые оптически активными, обладают способностью вызывать вращение плоскости поляризации проходящего через них плоскополяризованного света. К числу таких веществ относятся кристаллы кварц, киноварь и др, некоторые жидкости (скипидар, никотин), растворы оптически активных веществ в оптически неактивных растворителях (водные растворы сахара, винной кислоты и др.)

Угол поворота плоскости поляризации в твердых веществах пропорционален пути l, пройденному лучом в кристалле:

где α - постоянная оптического вращения, различная для разных веществ.

В растворах угол поворота плоскости поляризации пропорционален пути l, пройденному светом в растворе и концентрации с активного вещества:

Здесь [α] - удельная постоянная вращения.

В зависимости от направления вращения вещества подразделяются на право- и левовращающие. Существуют правый и левый кварц, правый и левый сахар и т.д. Молекулы или кристаллы одной модификации являются зеркальным отражением молекул или кристаллов другой модификации.

Если между двумя скрещенными поляризаторами поместить оптически активное вещество, то поле зрения просветляется. Чтобы снова затемнить его, надо повернуть один из поляризаторов на угол, определяемый соотношениями (4.1.99) или (4.11.100). Таким методом можно измерить концентрацию активного вещества в растворе, в частности, концентрацию сахара.

§ 19.12. Вектор электрической индукции. Кроме векторов е и р в электротехнических расчетах используют еще вектор электрической индукции, или вектор электрического смещения d.

§ 19.18. Выражение div e в цилиндрической и сферической системах координат.

§ 19.20. Граничные условия. Под граничными условиями понимают условия, которым подчиняется поле на границах раздела сред с разными электрическими свойствами.

§ 19.21 Поле внутри проводящего тела в условиях электростатики.

§ 19.23. Условия на границе раздела двух диэлектриков. На границе раздела двух диэлектриков с различными диэлектрическим проницаемостями выполняются два следующих условия:

§ 19.25. Общая характеристика задач электростатики и методов их решения. В зависимости от того, что задано и что определяют, задачи электростатики можно подразделить на три типа.

§ 19.35. Емкостные коэффициенты. Вторая группа формул Максвелла. Решим систему (19.48) относительно зарядов, полагая потенциалы φ и коэффициенты α известными:

§19.36. Частичные емкости. Третья группа формул Максвелла.

§19.37, Поле точечного заряда, расположенного вблизи проводящей сферы.

§ 19.38. Поле заряженной оси, расположенной параллельно цилиндру. Рассмотрим две родственные задачи на изображение в диэлектрическом и проводящем цилиндрах.

§19.39. Шар в равномерном поле. Если в равномерное поле (направлено сверху вниз: вдоль оси - z), напряженность которого

44 -

§ 19.40, Проводящий шар в равномерном поле. Для определения

§ 19.43. Понятие о плоскопараллельном, плоскомеридианном и равномерном полях. В литературе можно встретить термины «плоскопараллельное поле», «плоскомеридианное поле» и «равномерное

§ 19.44. Графическоепостроение картины плоскопараллельного поля.

§ 19.47. Энергия поля системы заряженных тел. Энергия поля, образованного системой п заряженных тел, имеющих потенциалы φ1.... Φn и заряды q1…..Qn

§ 19.48. Метод средних потенциалов. Как уже говорилось в электростатическом поле, образованном системой заряженных проводящих тел, все точки поверх-

§ 19.49. О расчете электрических полей, создаваемых диэлектриками, сохраняющими остаточную поляризацию при снятии внешнего поля. Поле, которое создает

123 341

§ 20.3. Первый закон Кирхгофа в дифференциальной форме.

§ 20.4. Дифференциальная форма закона Джоуля - Ленца. В гл. 1

§ 20.8. Экспериментальное исследование полей. Если форма гра- ничных поверхностей (электродов) сложна, то аналитический расчет

§ 21.3. Дифференциальная форма закона полного тока. Соотношение (21.3) пригодно для контура любых размеров, в том числе и для весьма малого.

§ 21.7. Выражение проекций ротора в цилиндрической и сферической системах координат. Без вывода приведем выражение проекций

§ 21.8. Принцип непрерывности магнитного потока и запись его в дифференциальной форме. Магнитный, поток есть поток вектора магнитной индукции через некоторую поверхность: ф = ∫ в dS.

2Ax= - μа X 2Ay= - μа y

2Az= - μа z

§ 21.14. Выражение магнитного потока через циркуляцию вектора-потенциала. Магнитный поток, пронизывающий какую-либо поверхность,

§ 21.17. Задачи, расчета магнитных полей. Рассмотрим некоторые типы

§ 21.18. Общая характеристика методов расчета и исследования

§ 21.19. Опытное исследование картины магнитного поля. Опытноеисследование картины магнитного поля производят различными методами.

§ 21.21. Магнитное экранирование, Положим, что в равномерном магнитном поле напряженностью н0 надо заэкранировать некоторую область пространства, например цилиндрическую, так, чтобы напря-

§ 21.26. Магнитное поле намагниченной пленки (ленты). Магнитная пленка

§ 21.28. Выражение механической силы в виде производной от энергии маг нитного поля по координате. Положим, что в системе из п контуров с токами

§ 22.2. Первое уравнение Максвелла. Первое уравнениеМаксвела записывают следующим образом Максвелла записывают следующим образом:■

§ 22.3. Уравнение непрерывности. Линии полного тока

§ 22.4. Второе уравнение Максвелла. Второе уравнение Максвелла

§ 22. 6 Теорема Умова - Пойнтинга для мгновенных значений.

§ 22.7. Теорема Умова -

§23.1. Уравнения Максаелла для проводящей среды. Рассмотрим особенности распространения электромагнитной волны в проводящей среде с проводимостью у и магнитной проницаемостью μа.

§23.3. Распространение плоской электромагнитной. Волны в однодном проводящем полупространстве. Рассмотрим вопрос о распространении плоской электромагнитной волны в однородной

§ 23.7. Неравномерное распределение тока в прямоугольной шине, находящейся в паазу электрической машины. Расположим оси декартовой системы в соответствии

§ 23.10. Экранирование в переменном электромагнитном поле.

§ 24.2. Плоские волны в однородных и изотропных полупроводящих средах.

§ 24.3. Граничные условия на поверхности раздела двух полупроводящих сред

§ 24.4. Переходные и релаксационные процессы в несовершенных диэлектриках. Процессы в полупроводящих средах должны удовлетворять уравнению непрерывности: .

§24.7. Тензор магнитной проницаемости феррита. Сначала вспомним, что, на зывают прецессией.

§ 25.1. Вывод уравнений для Аи φ в переменном электромагнит-

§25.3. Комплексная форма записи запаздывающего векторного потенциала. В гл. 21 [см. Уравнение (21.27)] отмечалось, что состав- ляющая векторного потенциала от элемента линейного тока idl

§ 25.4. Излучение электромагнитной энергии.

§ 26.5. Аналогия между волноводом и линией с распределенными параметрами.

§ 27.7. Движение заряженных частиц в кольцевых ускорителях. Циклотрон представляет собой две полые камеры в виде полуцилиндров нз проводящего неферро-

§ 28.2. Уравнения магнитной гидродинамики. Систему уравнений магнитной гидродинамики образуют следующие группы уравнений.

§ 28.3. Просачивание (диффузия) магнитного поля. Положим, что плазма неподвижна. Из уравнений (28.5) и (28.6) при V= 0 следует:

§ 28.7. Эффект сжатия (пинч-эффект). В цилиндрическом столбе электрической дуги (рис. 28.4) нити тока параллельны". Каждый элемент этой нити находится в маг-

§ 28.9. Принцип работы магнитного гидродинамического генератора. Через канал с большой скоростью V продувают плазму, нагретую до высокой температуры

Часть III

§ 22.2. Первое уравнение Максвелла. Первое уравнениеМаксвела записывают следующим образом Максвелла записывают следующим образом:■

В правой части его имеются две плотности тока: плотность тока проводимости и плотность тока электрического dD/dt. Ток электрического смещения возникает в любом диэлектрике, в том числе и в. вакууме, при изменении напряженности электрического поля во времени. Ток смещения порождает магнитное поле так же,как и ток проводимости. Хотя природа тока проводимости и тока смещения неодинакова, оба они обладают одним и тем же свойством - вызывать магнитное поле.

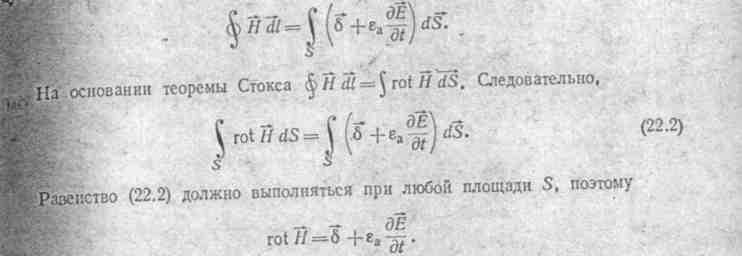
Таким образом, смысл первого уравнения Максвелла состоит

в том, что всякое изменение электрического смещения во времени (dD/dt)

в некоторой точке поля (т. е. возникновение в ней тока смещения) на таких же правах, как и ток проводимости, вызывает в этой точке вихрь магнитного поля (rot H), т. е. вызывает вихревое магнитное поле. Если среда однородна и изотропна, то ε а = const и тогда

С током смещения в предыдущих разделах (особенно в гл. 3 и 8) приходилось встречаться неоднократно. Так, известно,что при зарядке конденсатора через него протекает ток. Этот ток протекает через диэлектрик и является током смещения. Если, например, взять незаряженный плоский воздушный конденсатор и подключить его к источнику э. д. с. напряжением U через сопротивление R , то напряжение на обкладках конденсатора будет

Через поверхность S ток смещения в S раз больше, т. е. он равен току проводимости, протекающему по проводникам, соединяющим конденсатор с источником э. д. с.Отметим, что первое уравнение Максвелла представляет собой закон полного тока в дифференциальной форме.

Убедимся в том, что из закона полного тока следует уравнение (22.1). С этой целью возьмем произвольный контур и составим для него уравнение по закону полного тока. Полный ток, пронизывающий площадь, ограниченную контуром, равен сумме тока проводимости и тока смещения. Поэтому

§ 22.3. Уравнение непрерывности. Линии полного тока

являются непрерывными. Физически это означает, что на границе проводящей среды и диэлектрика ток проводимости переходит в ток смещения.

Можно математически сформулировать принцип непрерывности

(замкнутости) линий полного тока. С этой целью от обеих частей (22,1) дивергенция от ротора тождественно равна нулю (см. § 21.12).

Уравнение непрерывности (22.3") называют также законом сохра нения заряда. Этот закон означает, что электрический заряд неуничтожаем, он может только перемещаться из одного места в другое.

§ 22.4. Второе уравнение Максвелла. Второе уравнение Максвелла

записывают следующим образом:

Физический смысл его состоит в том, что всякое изменение магнитного

поля во времени (dB/dt) в какой-либо точке поля возбуждает вихрь или

ротор электрического поля в той же точке поля, т. е. вызывает вихревое

электрическое поле

Второе уравнение Максвела представляет собой дифференциальную форму закона электромагнитной индукции.

Для того чтобы убедиться в этом, проведем следующие рассуждения. Мысленно возьмем некоторый замкнутый контур, расположенный в переменном электромаг нитном поле. Переменный магнитный поток, пронизывающий контур, наведет в нем. э.д.с.

Равенство (22.5) должно выполняться при любых площадях S, что возможно только в том случае, когда равны подынтегральные функции- обоих интегралов. Следовательно,

rot E=

Знак «минус» в правой части второго уравнения Максвелла (как и в формуле

е= - d𝜓/dt) объясняется тем, что в основу положено правило правого винта. Если завинчивать правый винт так, что положительное направление вектора.магнитнойиндукции В в некоторой точке пространства при возрастании индукции этой точке совпадет с направлением движения острия винта, то положительное направление:для вектора напряженности электрического поля E при составлении циркуляции вектораЕ вдоль бесконечно малого контура, окружающего эту точку и лежащего,в плоскости, перпендикулярной векторуВ, совпадет с направлением вращения го- ловки винта.

Знак «минус» в правой части (22,4) поставлен для того, г чтобы привести в соответствие действительное направление для E при оговоренных ранее условиях с направлением, принятым для E за положительное.

Как в первом, так и во втором уравнениях Максвелла участвуют частные (не полные) производные во времени. Объясняется это тем, что уравнения Максвелла записаны для таких тел и контуров, кото рые неподвижны по отношению к выбранной системе координат. (Вопросы электродинамики движущихся сред кратко рассмотрены в § 22.9.)

В переменном электромагнитном поле кроме силовых линий элект-, рического поля, «начинающихся» и «оканчивающихся» на электриче- ских зарядах (как в электростатическом поле) могут быть и замкнутые на себя силовые линии электрического поля, охватывающие замкнутые на себя силовые линии магнитного Поля (см., например, рис. 26.5, а).

§ 22 5 Уравнения Максвелла в комплексной форме записи . Уравнения (22.1) и (22 4) записаны для мгновенных значении. Если H и E изменяются во времени синусоидально, то можно воспользоваться символическим методом и записать эти уравнения (22.1) и (22 4) в иной форме. Пусть H =Н т sin(ωt +𝜓 н) иЕ. =Е т sin(ωt +𝜓 E ). Можно записать Н=ImH m e iωt (Im- мнимая часть) или, условноH H m e iωt где комплексная амплитуда H m = H m e i 𝜓n . В свою очередьЕ E m e iωt значок соответствия). Так как напряженностиЕ и H, кроме того, что они меняются во семени по синусоидальному закону, являются функциями векторными т.е. определенным образом ориентированными в пространстве векторами то над ними ставят стрелку и точку:Ё т иН т . Стрелка означает, что речь идет о векторе в пространстве, точка - отом что проекции этого вектора на любую из координатных осей во времени изменяются синусоидально. Тогдаможно заменить на γ Ee iωt и