Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.

Введем новую физическую величину, характеризующую электрическое поле - поток Φ вектора напряженности электрического поля. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка ΔS . Произведение модуля вектора на площадь ΔS и на косинус угла α между вектором и нормалью к площадке называется элементарным потоком вектора напряженности через площадку ΔS (рис. 1.3.1):

Рассмотрим теперь некоторую произвольную замкнутую поверхность S . Если разбить эту поверхность на малые площадки ΔS i , определить элементарные потоки ΔΦi поля через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора через замкнутую поверхность S (рис. 1.3.2):

В случае замкнутой поверхности всегда выбирается внешняя нормаль .

Теорема Гаусса утверждает:

Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε 0 .

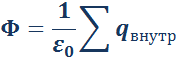
Для доказательства рассмотрим сначала сферическую поверхность S , в центре которой находится точечный заряд q . Электрическое поле в любой точке сферы перпендикулярно к ее поверхности и равно по модулю

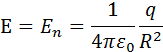
где R - радиус сферы. Поток Φ через сферическую поверхность будет равен произведению E на площадь сферы 4πR 2 . Следовательно,

Окружим теперь точечный заряд произвольной замкнутой поверхностью S и рассмотрим вспомогательную сферу радиуса R 0 (рис. 1.3.3).

Рассмотрим конус с малым телесным углом ΔΩ при вершине. Этот конус выделит на сфере малую площадку ΔS 0 , а на поверхности S - площадку ΔS . Элементарные потоки ΔΦ 0 и ΔΦ через эти площадки одинаковы. Действительно,

ΔΦ 0 = E 0 ΔS 0 , ΔΦ = E ΔS cos α = E ΔS " .

Здесь ΔS" = ΔS cos α - площадка, выделяемая конусом с телесным углом ΔΩ на поверхности сферы радиуса n .

Так как , a , следовательно Отсюда следует, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ 0 через поверхность вспомогательной сферы:

Аналогичным образом можно показать, что, если замкнутая поверхность S не охватывает точечного заряда q , то поток Φ = 0. Такой случай изображен на рис. 1.3.2. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, поэтому в этой области силовые линии не обрываются и не зарождаются.

Обобщение теоремы Гаусса на случай произвольного распределения зарядов вытекает из принципа суперпозиции. Поле любого распределения зарядов можно представить как векторную сумму электрических полей точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S будет складываться из потоков Φi электрических полей отдельных зарядов. Если заряд q i оказался внутри поверхности S , то он дает вклад в поток, равный если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю.

Таким образом, теорема Гаусса доказана.

Теорема Гаусса является следствием закона Кулона и принципа суперпозиции. Но если принять утверждение, содержащееся в этой теореме, за первоначальную аксиому, то ее следствием окажется закон Кулона. Поэтому теорему Гаусса иногда называют альтернативной формулировкой закона Кулона.

Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать.

Примером может служить задача о вычислении поля тонкостенного полого однородно заряженного длинного цилиндра радиуса R . Эта задача имеет осевую симметрию. Из соображений симметрии электрическое поле должно быть направлено по радиусу. Поэтому для применения теоремы Гаусса целесообразно выбрать замкнутую поверхность S в виде соосного цилиндра некоторого радиуса r и длины l , закрытого с обоих торцов (рис. 1.3.4).

При r ≥ R весь поток вектора напряженности будет проходить через боковую поверхность цилиндра, площадь которой равна 2πrl , так как поток через оба основания равен нулю. Применение теоремы Гаусса дает:

Этот результат не зависит от радиуса R заряженного цилиндра, поэтому он применим и к полю длинной однородно заряженной нити.

Для определения напряженности поля внутри заряженного цилиндра нужно построить замкнутую поверхность для случая r < R . В силу симметрии задачи поток вектора напряженности через боковую поверхность гауссова цилиндра должен быть и в этом случае равен Φ = E 2πrl . Согласно теореме Гаусса, этот поток пропорционален заряду, оказавшемуся внутри замкнутой поверхности. Этот заряд равен нулю. Отсюда следует, что электрическое поле внутри однородно заряженного длинного полого цилиндра равно нулю.

Аналогичным образом можно применить теорему Гаусса для определения электрического поля в ряде других случаев, когда распределение зарядов обладает какой-либо симметрией, например, симметрией относительно центра, плоскости или оси. В каждом из таких случаев нужно выбирать замкнутую гауссову поверхность целесообразной формы. Например, в случае центральной симметрии гауссову поверхность удобно выбирать в виде сферы с центром в точке симметрии. При осевой симметрии замкнутую поверхность нужно выбирать в виде соосного цилиндра, замкнутого с обоих торцов (как в рассмотренном выше примере). Если распределение зарядов не обладает какой-либо симметрией и общую структуру электрического поля угадать невозможно, применение теоремы Гаусса не может упростить задачу определения напряженности поля.

Рассмотрим еще один пример симметричного распределения зарядов - определение поля равномерно заряженной плоскости (рис. 1.3.5).

В этом случае гауссову поверхность S целесообразно выбрать в виде цилиндра некоторой длины, закрытого с обоих торцов. Ось цилиндра направлена перпендикулярно заряженной плоскости, а его торцы расположены на одинаковом расстоянии от нее. В силу симметрии поле равномерно заряженной плоскости должно быть везде направлено по нормали. Применение теоремы Гаусса дает:

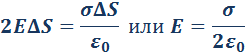
где σ - поверхностная плотность заряда , т. е. заряд, приходящийся на единицу площади.

Полученное выражение для электрического поля однородно заряженной плоскости применимо и в случае плоских заряженных площадок конечного размера. В этом случае расстояние от точки, в которой определяется напряженность поля, до заряженной площадки должно быть значительно меньше размеров площадки.

Когда зарядов много, при расчётах полей возникают некоторые трудности.

Преодолеть их помогает теорема Гаусса. Суть теоремы Гаусса сводится к следующему: если произвольное количество зарядов мысленно окружить замкнутой поверхностью S, то поток напряжённости электрического поля через элементарную площадку dS можно записать как dФ = Есоsα۰dS где α - угол между нормалью к плоскости и вектором напряжённости . (рис.12.7)

Полный же поток через всю поверхность будет равен сумме потоков от всех зарядов, произвольным образом распределённых внутри её и пропорционально величине этого заряда

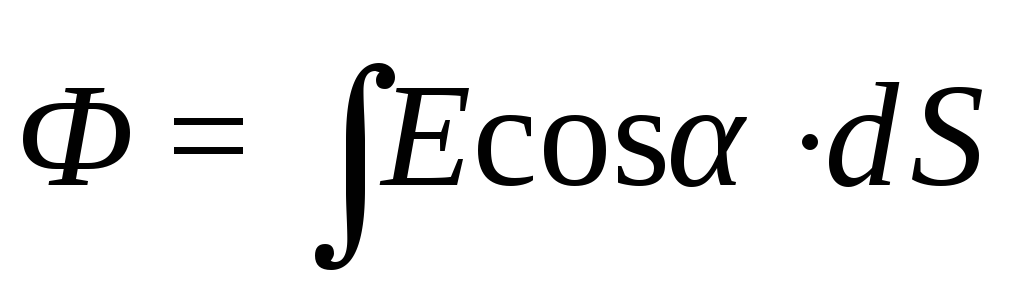(12.9)

Определим поток вектора напряжённости сквозь сферическую поверхность радиуса r, в центре которой расположен точечный заряд +q (рис.12.8). Линии напряжённости перпендикулярны поверхности сферы, α =0, следовательно соsα = 1. Тогда

Если поле образовано системой зарядов, то

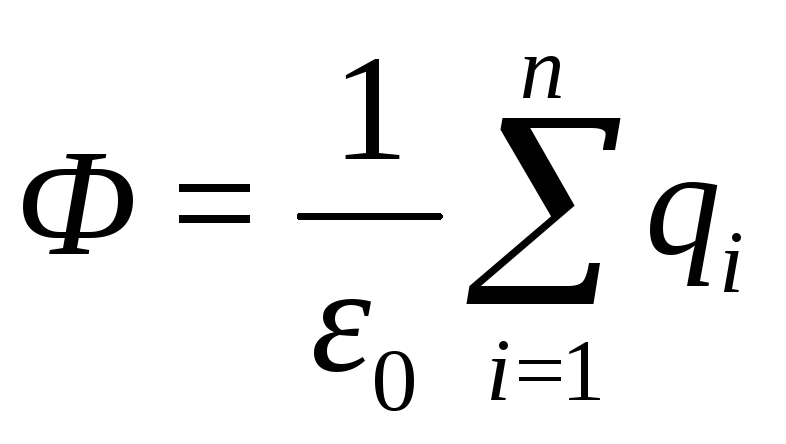
Теорема Гаусса: поток вектора напряжённости электростатического поля в вакууме сквозь любую замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, делённой на электрическую постоянную.

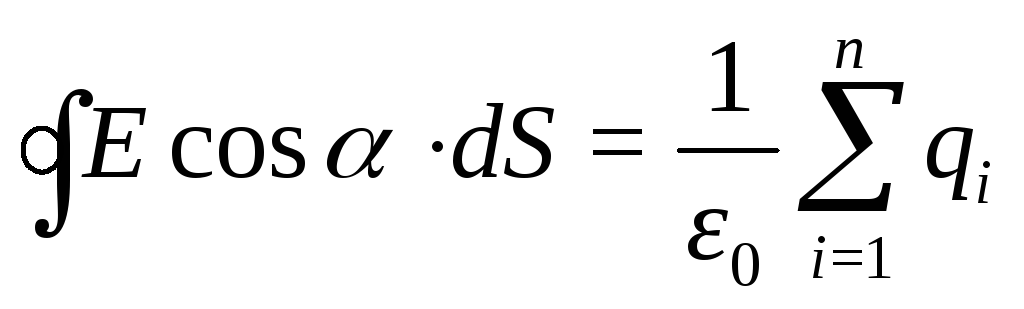(12.10)

Если внутри сферы зарядов нет, то Ф = 0.

Теорема Гаусса позволяет сравнительно просто рассчитать электрические поля при симметрично распределённых зарядов.

Введём понятие о плотности распределенных зарядов.

Линейная плотность обозначается τ и характеризует заряд q, приходящийся на единицу длины ℓ. В общем виде может быть рассчитана по формуле

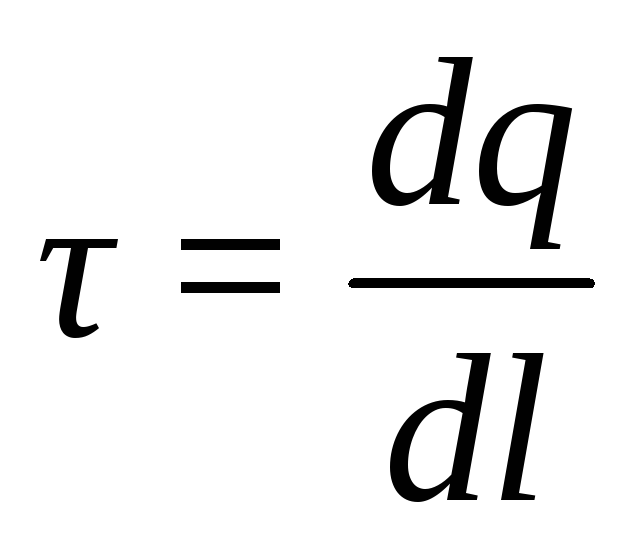(12.11)

При равномерном распределении зарядов линейная плотность равна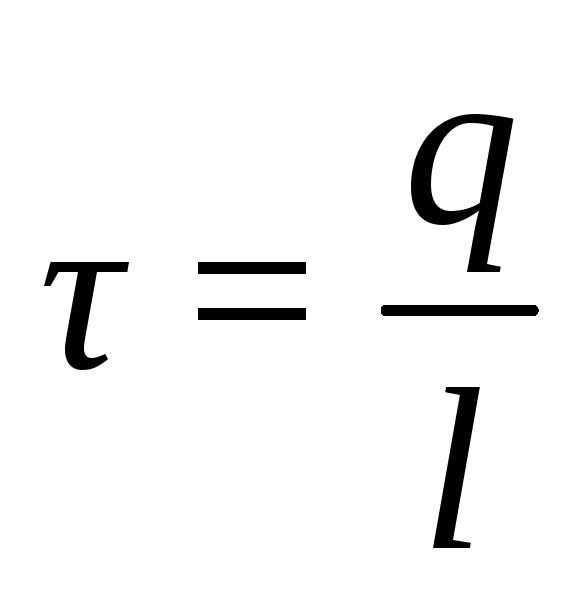

Поверхностная плотность обозначается σ и характеризует заряд q, приходящийся на единицу площади S. В общем виде определяется по формуле

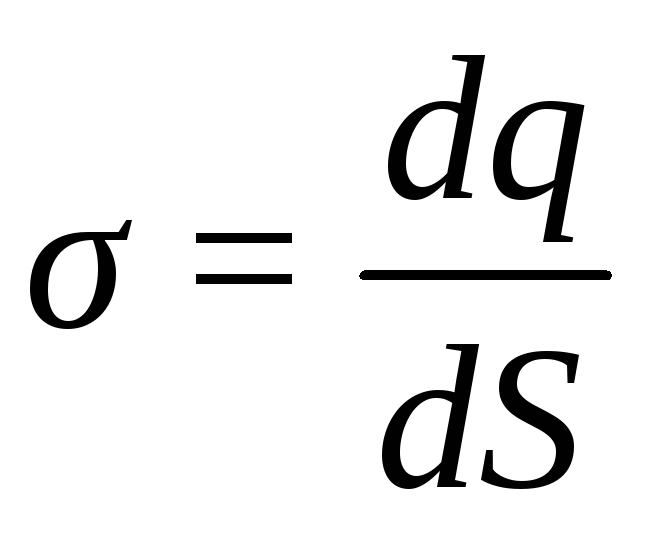(12.12)

При равномерном распределении зарядов по поверхности поверхностная плотность равна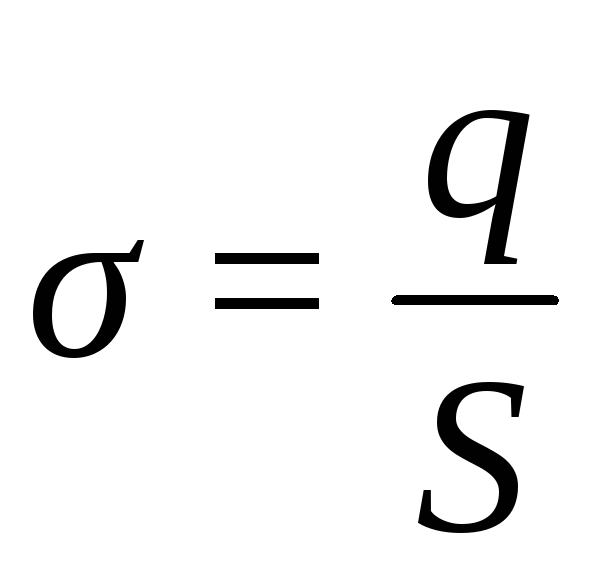

Объёмная плотность обозначается ρ, характеризует заряд q, приходящийся на единицу объёма V. В общем виде определяется по формуле

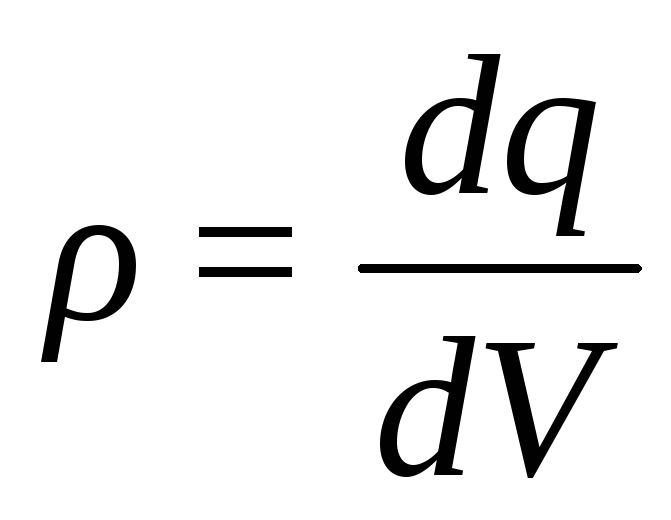(12.13)

При равномерном распределении зарядов она равна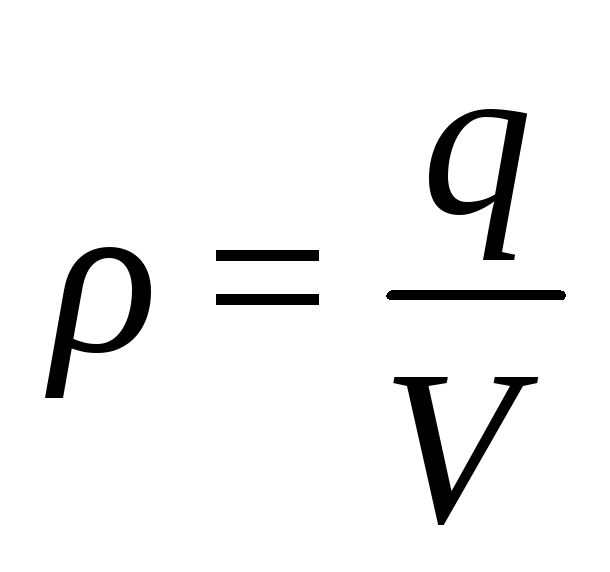

.

Так как заряд q располагается на сфере равномерно, то

σ = const. Применим теорему Гаусса. Проведём сферу радиусом через точку А. Поток вектора напряжённости рис.12.9 сквозь сферическую поверхность радиуса равен соsα = 1, так как α = 0. По теореме Гаусса,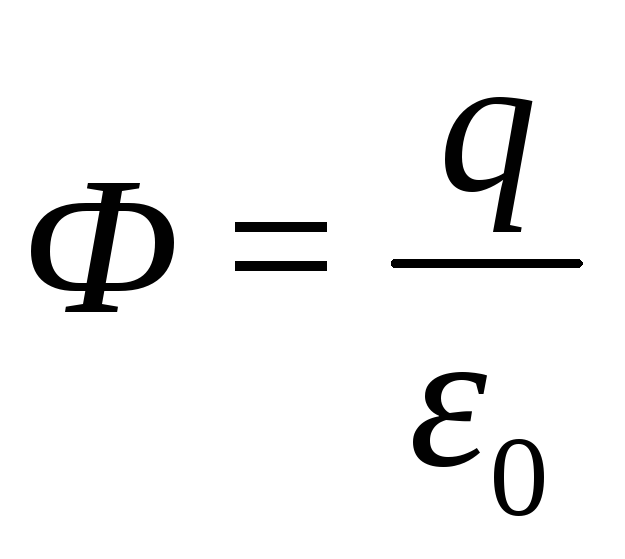

.

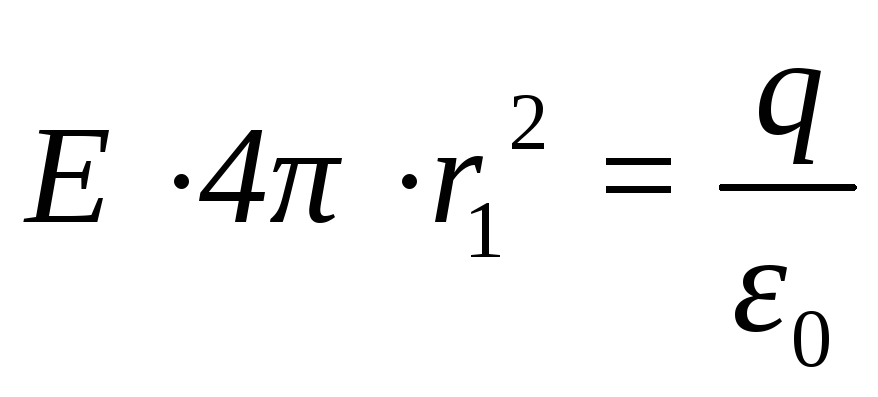или

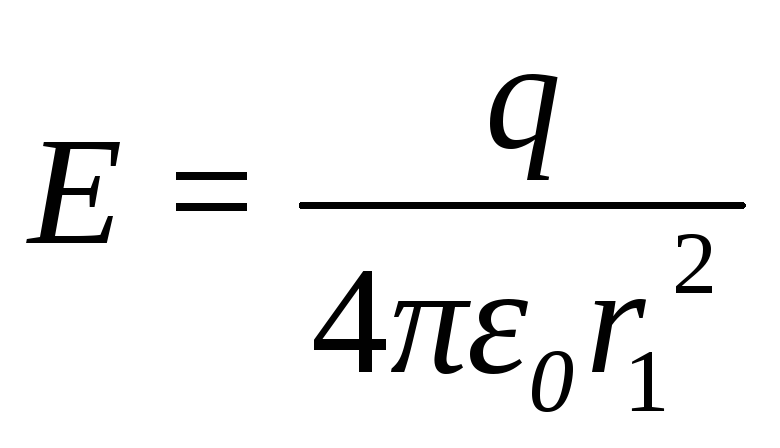(12.14)

Из выражения (12.14) следует, что напряжённость поля вне заряженной сферы такая же, как напряжённость поля точечного заряда, помещённого в центре сферы. На поверхности сферы, т.е. r 1 = r 0 , напряжённость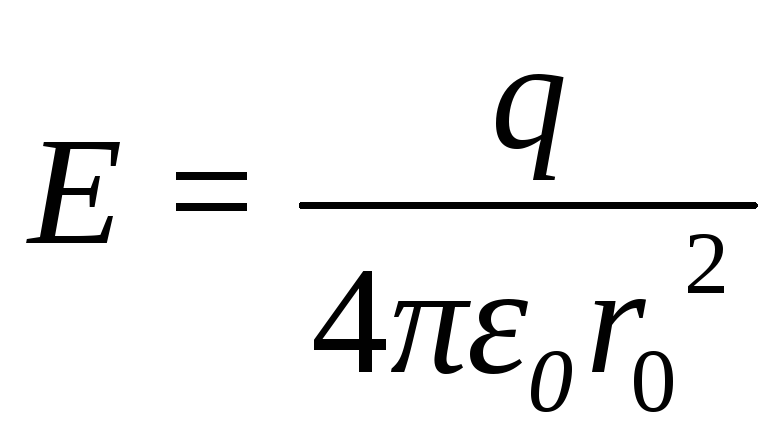

.

Внутри сферы r 1 < r 0 (рис.12.9) напряжённость Е = 0, так как сфера радиусом r 2 внутри никаких зарядов не содержит и, по теореме Гаусса, поток вектора сквозь такую сферу равен нулю.

Цилиндр радиусом r 0 равномерно заряжен с поверхностной плотностью σ (рис.12.10). Определим напряжённость поля в произвольно выбранной точке А. Проведём через точку А воображаемую цилиндрическую поверхность радиусом R и длиной ℓ. Вследствие симметрии поток будет выходить только через боковые поверхности цилиндра, так как заряды на цилиндре радиуса r 0 распределены по его поверхности равномерно, т.е. линии напряжённости будут радиальными прямыми, перпендикулярными боковым поверхностям обоих цилиндров. Так как поток через основание цилиндров равен нулю (cos α = 0), а боковая поверхность цилиндра перпендикулярна силовым линиям (cos α = 1), то

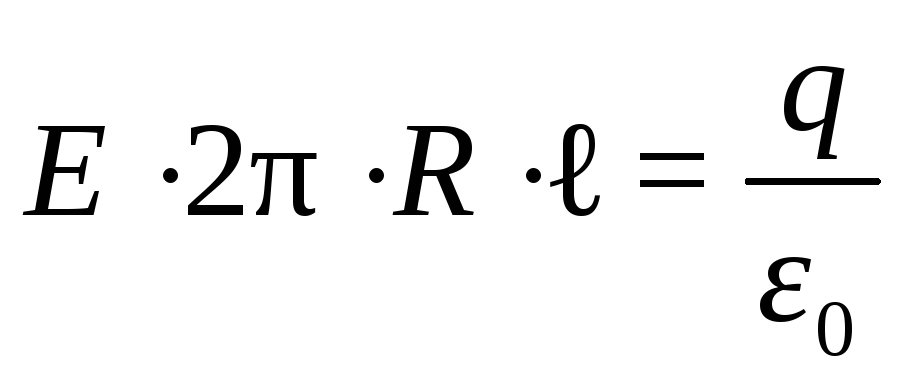или

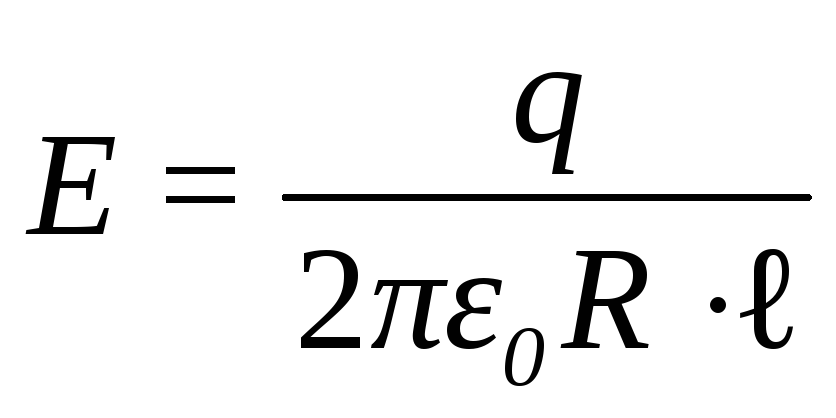(12.15)

Выразим величину Е через σ - поверхностную плотность. По определению,

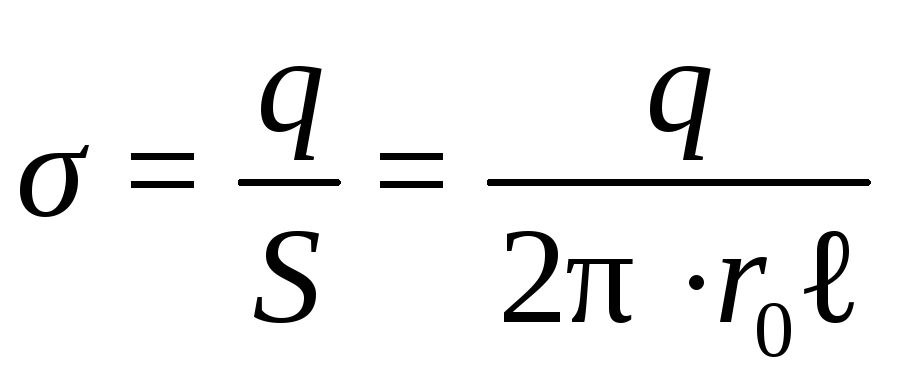следовательно,

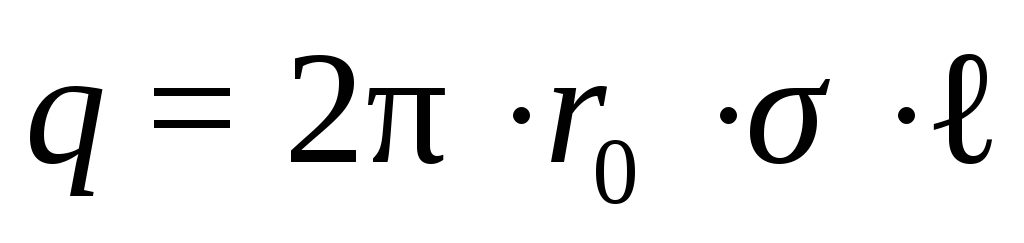
Подставим значение q в формулу (12.15)

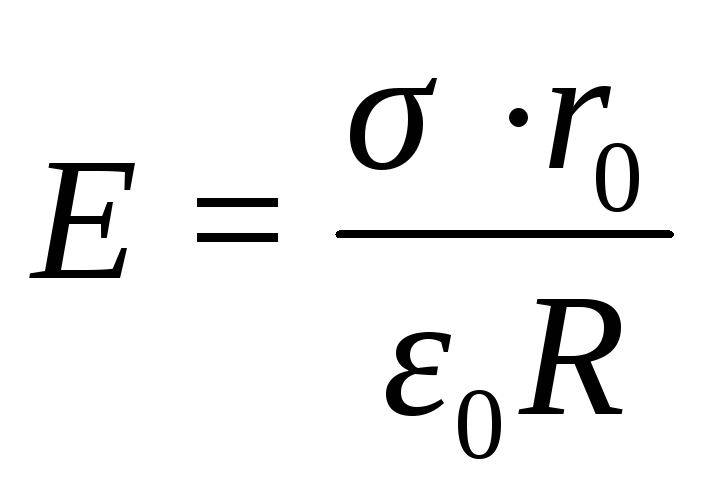(12.16)

По определению линейной плотности,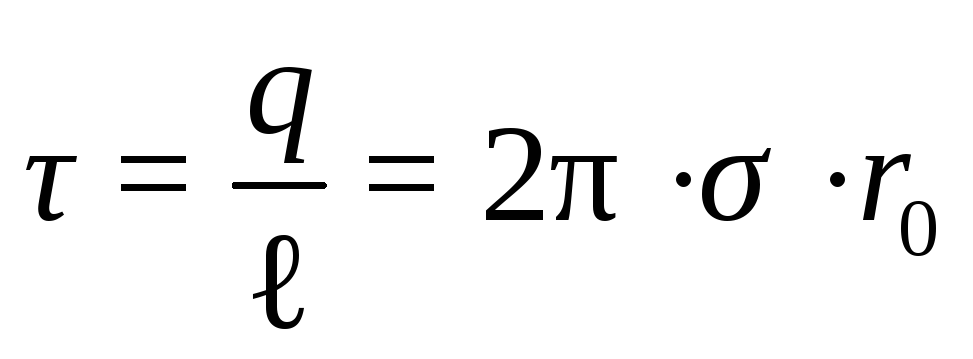

, откуда

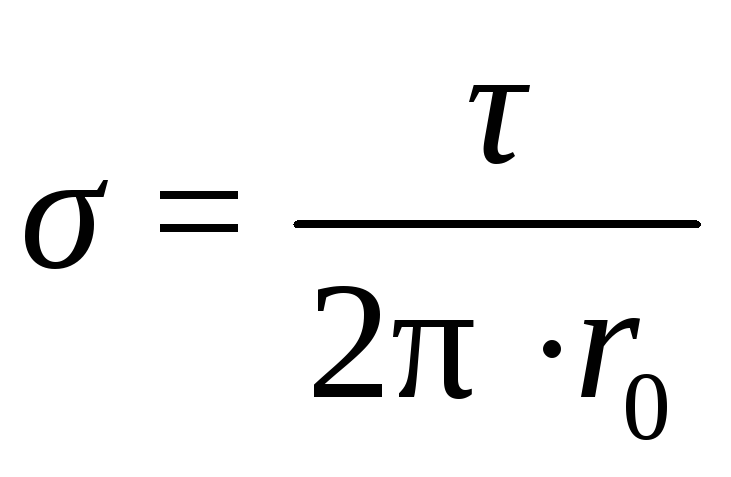; подставляем это выражение в формулу (12.16):

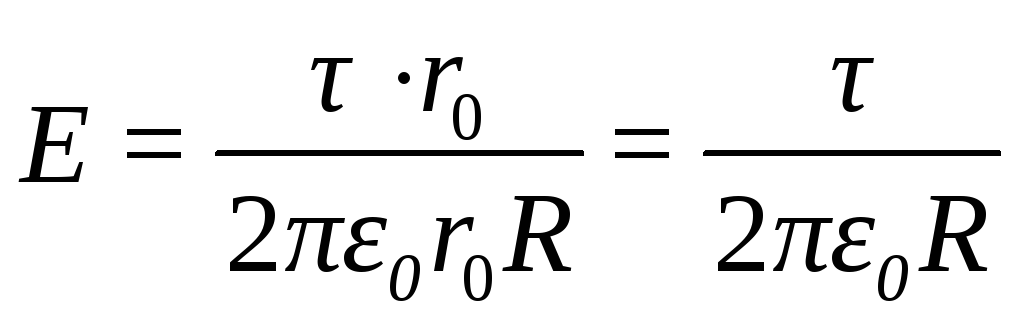(12.17)

т.е. напряжённость поля, создаваемого бесконечно длинным заряженным цилиндром, пропорциональна линейной плотности заряда и обратно пропорциональна расстоянию.

Напряжённость поля, создаваемого бесконечной равномерно заряженной плоскостью

Определим напряжённость поля, создаваемого бесконечной равномерно заряженной плоскостью в точке А. Пусть поверхностная плотность заряда плоскости равна σ. В качестве замкнутой поверхности удобно выбрать цилиндр, ось которого перпендикулярна плоскости, а правое основание содержит точку А. Плоскость делит цилиндр пополам. Очевидно, что силовые линии перпендикулярны плоскости и параллельны боковой поверхности цилиндра, поэтому весь поток проходит только через основания цилиндра. На обоих основаниях напряжённость поля одинакова, т.к. точки А и В симметричны относительно плоскости. Тогда поток, через основания цилиндра равен

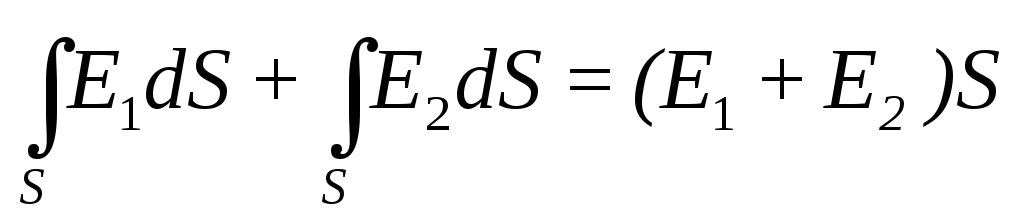
Согласно теореме Гаусса,

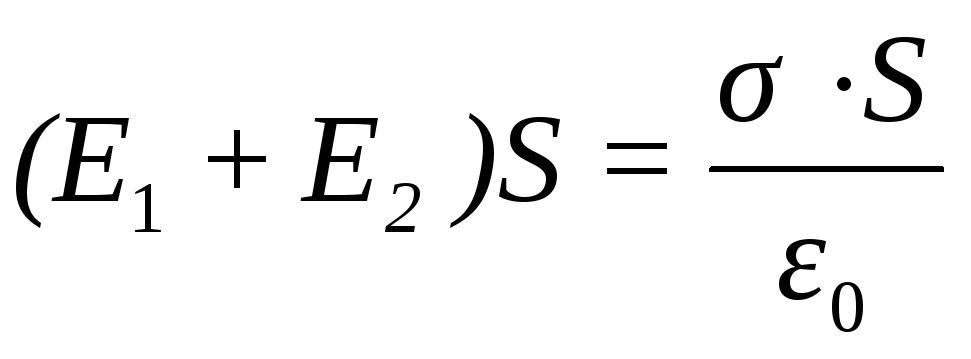
Так как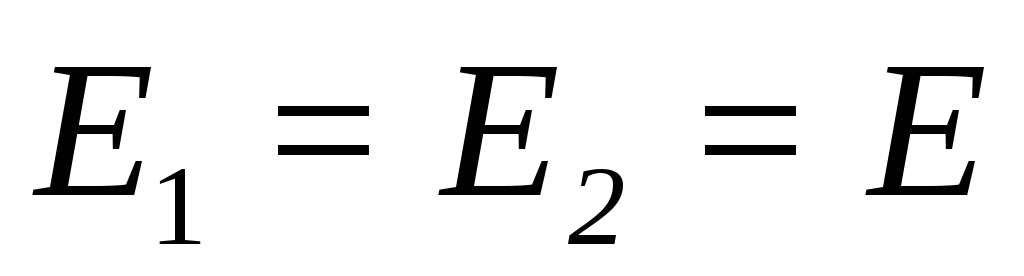

, то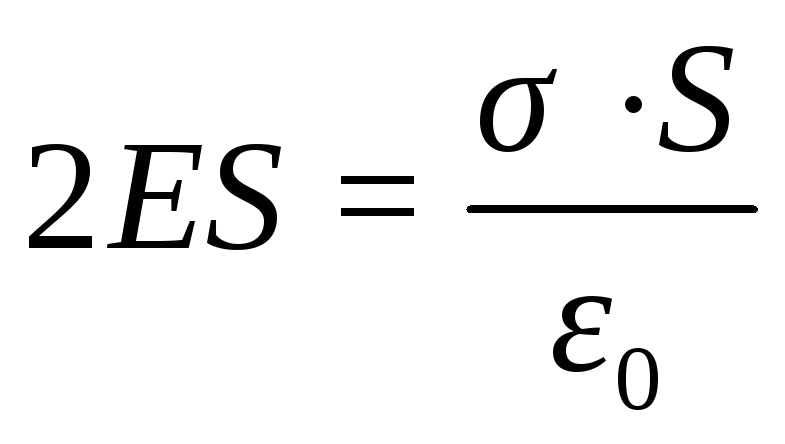

, откуда

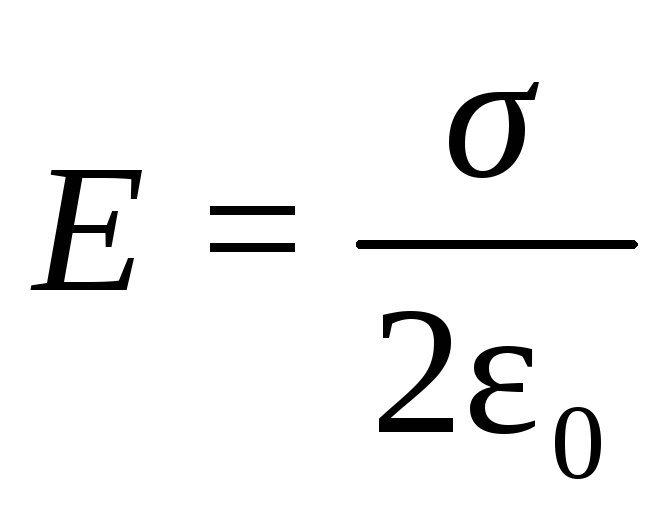(12.18)

Таким образом, напряжённость поля бесконечной заряженной плоскости пропорциональна поверхностной плотности заряда и не зависит от расстояния до плоскости. Следовательно, поле плоскости является однородным.

Напряжённость поля, создаваемого двумя разноименно равномерно заряженными параллельными плоскостями

Результирующее поле, создаваемое двумя плоскостями, определяется по принципу суперпозиции полей: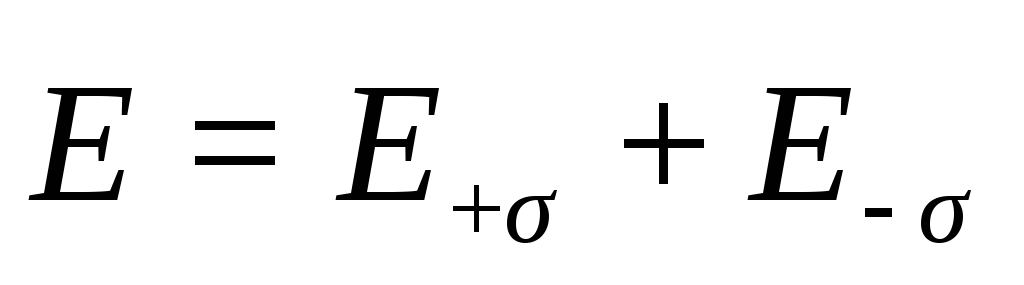

(рис.12.12). Поле, создаваемое каждой плоскостью, является однородным, напряжённости этих полей равны по модулю, но противоположны по направлению:

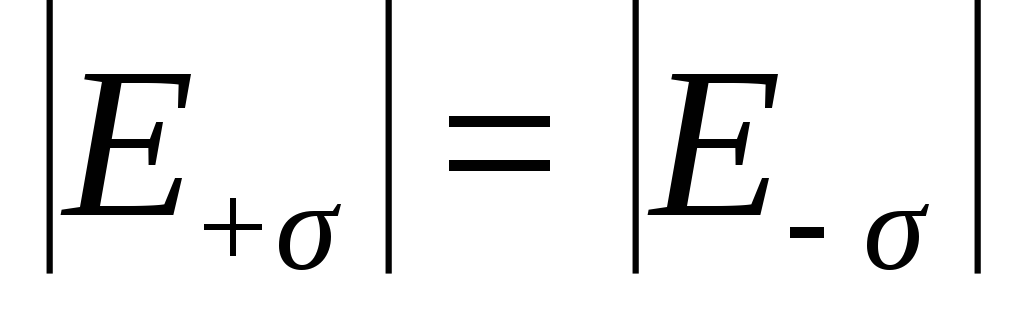. По принципу суперпозиции напряжённость суммарного поля вне плоскости равна нулю:

Между плоскостями напряжённости полей имеют одинаковые направления, поэтому результирующая напряжённость равна

Таким образом, поле между двумя разноименно равномерно заряженными плоскостями однородно и его напряжённость в два раза больше, чем напряжённость поля, создаваемого одной плоскостью. Слева и справа от плоскостей поле отсутствует. Такой же вид имеет и поле конечных плоскостей, искажение появляется только вблизи их границ. С помощью полученной формулы можно рассчитать поле между обкладками плоского конденсатора.

Принцип суперпозиции в сочетании с законом Кулона даёт ключ к вычислению электрического поля произвольной системы зарядов, но непосредственное суммирование полей по формуле (4.2) обычно требует сложных вычислений. Впрочем, при наличии той или иной симметрии системы зарядов вычисления существенно упрощаются, если ввести понятие потока электрического поля и использовать теорему Гаусса.

Представления о потоке электрического поля привнесены в электродинамику из гидродинамики. В гидродинамике поток жидкости через трубу, то есть объём жидкости N , проходящий через сечение трубы в единицу времени, равен v ⋅ S , где v — скорость жидкости, а S — площадь сечения трубы. Если скорость жидкости изменяется по сечению, нужно использовать интегральную формулу N = ∫ S v → ⋅ d S → . Действительно, выделим в поле скоростей малую площадку d S , перпендикулярную к вектору скорости (рис. ).

Рис. 1.4: Поток жидкости

Объём жидкости, протекающий через эту площадку за время d t , равен v d S d t . Если площадка наклонена к потоку, то соответствующий объём будет v d S cos θ d t , где θ — угол между вектором скорости v → и нормалью n → к площадке d S . Объём жидкости, протекающий через площадку d S в единицу времени получается делением этой величины на d t . Он равен v d S cos θ d t , т.е. скалярному произведению v → ⋅ d S → вектора скорости v → на вектор элемента площади d S → = n → d S . Единичный вектор n → нормали к площадке d S можно провести в двух прямо противоположных направлениях. одно из них условно принимается за положительное. В этом направлении и проводится нормаль n → . Та сторона площадки, из которой выходит нормаль n → , называется внешней, а та, в которую нормаль n → входит, — внутренней. Вектор элемента площади d S → направлен по внешней нормали n → к поверхности, а по величине равен площади элемента d S = ∣ d S → ∣ . При вычислении объёма протекающей жидкости через площадку S конечных размеров, её надо развить на бесконечно малые площадки d S , а затем вычислить интеграл ∫ S v → ⋅ d S → по всей поверхности S .

Выражения типа ∫ S v → ⋅ d S → встречаются во многих отраслях физики и математики. Они называются потоком вектора v → через поверхность S независимо от природы вектора v → . В электродинамике интеграл

N = ∫ S E → ⋅ d S →

(5.1)

называют потоком напряженности электрического поля E → через произвольную поверхность S , хотя с этим понятием не связано никакое реальное течение.

Допустим, что вектор E → представляется геометрической суммой

E → = ∑ j E → j .

Умножив это равенство скалярно на d S → и проинтегрировав, получим

N = ∑ j N j .

где N j — поток вектора E → j через ту же самую поверхность. Таким образом, из принципа суперпозиции напряженности электрического поля следует, что потоки через одну и ту же поверхность складываются алгебраически.

Теорема Гаусса гласит, что поток вектора E → через произвольную замкнутую поверхность равен умноженному на 4 π суммарному заряду Q всех частиц, находящихся внутри этой поверхности:

Доказательство теоремы проведем в три этапа.

1. Начнем с вычисления потока электрического поля одного точечного заряда q (рис. ). В простейшем случае, когда поверхность интегрирования S является сферой, а заряд находится в её центре, справедливость теоремы Гаусса практически очевидна. На поверхности сферы напряженность электрического поля

E → = q r → ∕ r 3

постоянна по величине и всюду направлена по нормали к поверхности, так что поток электрического поля просто равен произведению E = q ∕ r 2 на площадь сферы S = 4 π r 2 . Следовательно, N = 4 π q . Этот результат не зависит от формы поверхности, окружающей заряд. Чтобы доказать это, выделим произвольную площадку поверхности достаточно малого размера с установленным на ней направлением внешней нормали n → . На рис. показан один такой сегмент преувеличенно большого (для наглядности) размера.

Поток вектора E → через эту площадку равен d N = E → ⋅ d S → = E cos θ d S ,

где θ — угол между направлением E → и внешней нормалью n → к площадке d S . Так как E = q ∕ r 2 , а d S cos θ ∕ r 2 по абсолютной величине есть элемент телесного угла d Ω = d S ∣ cos θ ∣ ∕ r 2 , под которым видна площадка d S из точки расположения заряда,

D N = ± q d Ω .

где знаки плюс и минус отвечают знаку cos θ , а именно: следует взять знак плюс, если вектор E → составляет острый угол с направлением внешней нормали n → , и знак минус в противном случае.

2. Теперь рассмотрим конечную поверхность S , охватывающую некоторый выделенный объём V . По отношению к этому объёму всегда можно определить, какое из двух противоположных направлений нормали к любому элементу поверхности S следует считать внешним. Внешняя нормаль направлена из объёма V наружу. Суммируя по сегментам, с точностью до знака имеем N = q Ω , где Ω — телесный угол, под которым видна поверхность S из точки, где находится заряд q . Если поверхность S замкнута, то Ω = 4 π при условии, что заряд q находится внутри S . В противном случае Ω = 0 . Чтобы пояснить последнее утверждение, можно вновь обратиться к рис. .

Очевидно, что потоки через сегменты замкнутой поверхности, опирающиеся на равные телесные углы, но обращенные в противоположные стороны, взаимно сокращаются. Очевидно также, что если заряд находится вне замкнутой поверхности, то любому сегменту, обращенному наружу, найдется соответствующий сегмент, обращенный внутрь.

3. Наконец, воспользовавшись принципом суперпозиции, приходим к итоговой формулировке теоремы Гаусса (). Действительно, поле системы зарядов равно сумме полей каждого заряда в отдельности, но в правую часть теоремы () дают ненулевой вклад только заряды, находящиеся внутри замкнутой поверхности. Этим завершается доказательство.

В макроскопических телах число носителей заряда столь велико, что дискретный ансамбль частиц удобно представить в виде непрерывного распределения, введя понятие плотности заряда. По определению, плотностью заряда ρ называется отношение Δ Q ∕ Δ V в пределе, когда объём Δ V стремится к физически бесконечно малой величине:

где интегрирование в правой части производится по объему V , замкнутому поверхностью S .

Теорема Гаусса даёт одно скалярное уравнение на три компоненты вектора E → , поэтому для расчета электрического поля одной этой теоремы недостаточно. Необходима известная симметрия распределения плотности зарядов, чтобы задача могла быть сведена к одному скалярному уравнению. Теорема Гаусса позволяет найти поле в тех случаях, когда поверхность интегрирования в () удается выбрать так, что напряженность электрического поля E постоянна на всей поверхности. Рассмотрим наиболее поучительные примеры.

▸ Задача 5.1

Найти поле шара, равномерно заряженного по объёму или поверхности.

Решение: Электрическое поле точечного заряда E → = q r → ∕ r 3 стремится к бесконечности при r → 0 . Этот факт показывает противоречивость представления элементарных частиц точечными зарядами. Если же заряд q равномерно распределен по объему шара конечного радиуса a , то электрическое поле не имеет особенностей.

Из симметрии задачи ясно, что электрическое поле E → всюду направлено радиально, а его напряженность E = E (r) зависит только от расстояния r до центра шара. Тогда поток электрического поля через сферу радиуса r просто равен 4 π r 2 E (рис. ).

С другой стороны, заряд внутри той же сферы равен полному заряду шара Q , если r ≥ a . Приравнивая 4 π r 2 E к умноженному на 4 π заряду шара q , получаем: E (r) = q ∕ r 2 .

Таким образом, во внешнем пространстве заряженный шар создает такое поле, как если бы весь заряд был сосредоточен в его центре. Этот результат справедлив при любом сферически симметричном распределении заряда.

Поле внутри шара равно E (r) = Q ∕ r 2 , где Q — заряд внутри серы радиуса r . Если заряд равномерно распределен по объему шара, то Q = q (r ∕ a) 3 . В этом случае

E (r) = q r ∕ a 3 = (4 π ∕ 3) ρ r ,

где ρ = q ∕ (4 π a 3 ∕ 3) — плотность заряда. Внутри шара поле линейно спадает от максимального значения на поверхности шара до нуля в его центре (рис. ).

Функция E (r) при этом всюду конечна и непрерывна.

Если заряд распределен по поверхности шара, то Q = 0 , а поэтому также E = 0 . Это результат также справедлив для случая, когда внутри сферической полости зарядов нет, а внешние заряды распределены сферически симметрично. ▸ Задача 5.2

Найти поле равномерно заряженной бесконечной нити; радиус нити a , заряд на единицу длины ϰ .

▸ Задача 5.3

Найти поле бесконечной прямой нити и бесконечно длинного равномерно заряженного цилиндра.

▸ Задача 5.4

Найти поле бесконечной заряженной плоскости и равномерно заряженного бесконечного плоского слоя.

Решение: Вследствие симметрии задачи поле направлено по нормали к слою и зависит только от расстояния x от плоскости симметрии пластины. Для вычисления поля с помощью теоремы Гаусса удобно выбрать поверхность интегрирования S в виде параллелипипеда, как показано на рис. .

Последний результат получается предельным переходом a → 0 при одновременном увеличении плотности заряда ρ так, чтобы величина σ = ρ a оставалась неизменной. По разные стороны от плоскости напряженность электрического поля одинакова по величине, но противоположна по направлению. Поэтому при переходе через заряженную плоскость поле скачком меняется на величину 4 π σ . Заметим, что пластина может считаться бесконечной, если расстояние от пренебрежимо мало по сравнению с её размерами. На расстояниях очень больших по сравнению с размерами пластины она действует, как точечный заряд, и её поле убывает обратно пропорционально квадрату расстояния.

Теорема Гаусса устанавливает точное соотношение между потоком напряженности электрического поля через замкнутую поверхность и суммарным зарядом Q внутри этой поверхности:

где ε 0 - та же константа (электрическая постоянная), что и в законе Кулона.
Подчеркнем, что Q - это заряд, заключенный внутри той поверхности, по которой берется интеграл в левой части. При этом не существенно, как именно распределен заряд внутри поверхности; заряды вне поверхности не учитываются. (Внешний заряд может повлиять на расположение силовых линий, но не на алгебраическую сумму линий, входящих внутрь поверхности и выходящих наружу.

Прежде чем переходить к обсуждению теоремы Гаусса, заметим, что интеграл по поверхности на практике не всегда легко вычисляется, однако необходимость в этом возникает не часто, за исключением самых простых ситуаций, которые мы рассмотрим ниже

Как же связаны между собой теорема Гаусса и закон Кулона? Покажем вначале, что закон Кулона следует из теоремы Гаусса. Рассмотрим уединенный точечный заряд Q . По предположению теорема Гаусса справедлива для произвольной замкнутой поверхности. Выберем поэтому такую поверхность, с которой удобнее всего иметь дело: симметричную поверхность сферы радиусом r , в центре которой находится наш заряд Q (рис. 23.7).

Поскольку сфера (конечно, воображаемая) симметрична относительно заряда, расположенного в ее центре, напряженность электрического поля Е должна иметь одно и то же значение в любой точке сферы; кроме того, вектор Е всюду направлен наружу (или всюду внутрь) параллельно вектору dA элемента поверхности. Тогда равенство

принимает вид

(площадь сферы радиусом r равна 4πr 2). Отсюда находим

В итоге мы получили закон Кулона.

Теперь об обратном. В общем случае теорему Гаусса нельзя вывести из закона Кулона: теорема Гаусса является более общим (и более тонким) утверждением, нежели закон Кулона. Однако для некоторых частных случаев теорему Гаусса удается получить из закона Кулона; мы используем общие рассуждения относительно силовых линий. Рассмотрим для начала уединенный точечный заряд, окруженный сферической поверхностью (рис. 23.7). Согласно закону Кулона, напряженность электрического поля в точке на поверхности сферы равна

Е = (1 /4πε 0)(Q/r)

Проделав в обратном порядке аналогичные рассуждения, получим

Это и есть теорема Гаусса, и мы вывели ее для частного случая точечного заряда в центре сферической поверхности. Но что можно сказать о поверхности неправильной формы, например поверхности А 2 на рис. 23.8 . 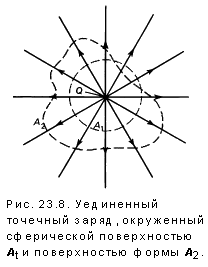Через эту поверхность проходит то же число силовых линий, что и через сферу А 1 , но поскольку поток напряженности электрического поля через поверхность пропорционален числу проходящих через нее силовых линий, поток через А 2 равен потоку через А 1 .

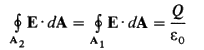
Следует ожидать поэтому, что формула

справедлива для любой замкнутой поверхности, окружающей точечный заряд.

Рассмотрим, наконец, случай, когда внутри поверхности находится не единственный заряд. Для каждого заряда в отдельности

Но коль скоро полная напряженность электрического поля Е есть сумма напряженностей, обусловленных отдельными зарядами, , то

где - суммарный заряд, заключенный внутри поверхности.
Итак, эти простые рассуждения подсказывают нам, что теорема Гаусса справедлива для любого распределения электрических зарядов внутри любой замкнутой поверхности. Следует иметь в виду, однако, что поле Е не обязательно обусловлено только зарядами Q , которые находятся внутри поверхности. Например, на рис. 23.3 рассмотренном ранее, электрическое поле Е существует во всех точках поверхности, однако оно создается вовсе не зарядом внутри поверхности (здесь Q = 0). Теорема Гаусса справедлива для потока напряженности электрического поля через любую замкнутую поверхность; она утверждает, что если поток, направленный внутрь поверхности, не равен потоку, направленному наружу, то это обусловлено наличием зарядов внутри поверхности.

Теорема Гаусса справедлива для любого векторного поля, обратно пропорционального квадрату расстояния, например, для гравитационного поля. Но для полей другого типа она не будет выполняться. Допустим, например, что поле точечного заряда убывает как kQ/r ; тогда поток через сферу радиусом r определялся бы выражением

Чем больше радиус сферы, тем больше был бы поток, несмотря на то что заряд внутри сферы остается постоянным.

Применения теоремы Гаусса

Теорема Гаусса позволяет выразить связь между электрическим зарядом и напряженностью электрического поля в очень компактной и элегантной форме. С помощью этой теоремы удается легко найти напряженность поля в случае, когда распределение зарядов оказывается достаточно простым и симметричным. При этом, однако, необходимо позаботиться о надлежащем выборе поверхности интегрирования. Обычно стремятся выбрать поверхность так, чтобы напряженность электрического поля Е была постоянна по всей поверхности, или по крайней мере на определенных ее участках.

Чтобы получить эти результаты на основании закона Кулона, нам пришлось бы потрудиться, интегрируя по объему шара. Благодаря использованию теоремы Гаусса и симметрии задачи решение оказалось почти тривиальным. Это демонстрирует огромные возможности теоремы Гаусса. Однако подобное использование этой теоремы ограничено в основном случаями, когда распределение зарядов обладает высокой симметрией. В подобных ситуациях мы выбираем простую поверхность, на которой Е = const , и интеграл берется без труда. Разумеется, теорема Гаусса справедлива для любой поверхности, «простые» поверхности выбираются лишь для облегчения интегрирования.

Заключение

Поток напряженности однородного электрического поля Е через плоскую площадку А равен Ф E = Е А . Если поле неоднородно, то поток определяется интегралом Ф E = ∫Е dA .
Вектор А (или dA ) направлен перпендикулярно площадке А (или dA ); для замкнутой поверхности вектор А направлен наружу. Поток через поверхность пропорционален числу силовых линий, проходящих через эту поверхность.

Теорема Гаусса утверждает, что результирующий поток напряженности электрического поля, проходящий через замкнутую поверхность, равен суммарному заряду внутри поверхности, деленному на ε 0 :

В принципе теорему Гаусса можно использовать для определения напряженности электрического поля, создаваемого заданным распределением зарядов. Однако на практике ее применение ограничено в основном несколькими частными случаями, когда распределение зарядов имеет высокую симметрию. Истинная ценность теоремы Гаусса состоит в том, что она устанавливает в более общем и более элегантном виде, чем закон Кулона, связь между электрическим зарядом и напряженностью электрического поля. Теорема Гаусса является одним из фундаментальных уравнений электромагнитной теории.

Продолжение следует. Коротко о следующей публикации:

Замечания и предложения принимаются по адресу [email protected]

Эта теорема представляет собой только следствие закона Кулона и принципа суперпозиции электрических полей. Вот её формулировка:

Поток вектора напряжённости электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме электрических зарядов, заключённых внутри этой поверхности, делённой на электрическую постоянную e 0 .

Доказательство теоремы начнём с простейшего случая: вычислим поток вектора напряжённости поля точечного заряда Q .

Напряжённость этого поля хорошо известна (см. 1.3)

Учитывая сферическую симметрию поля, выберем вначале в качестве гауссовой замкнутой поверхности сферу радиусом r , с центром в той точке, где находится заряд Q (рис. 2.5., 1). Поток вектора напряжённости через эту поверхность вычислить легко

Здесь мы учли, что:

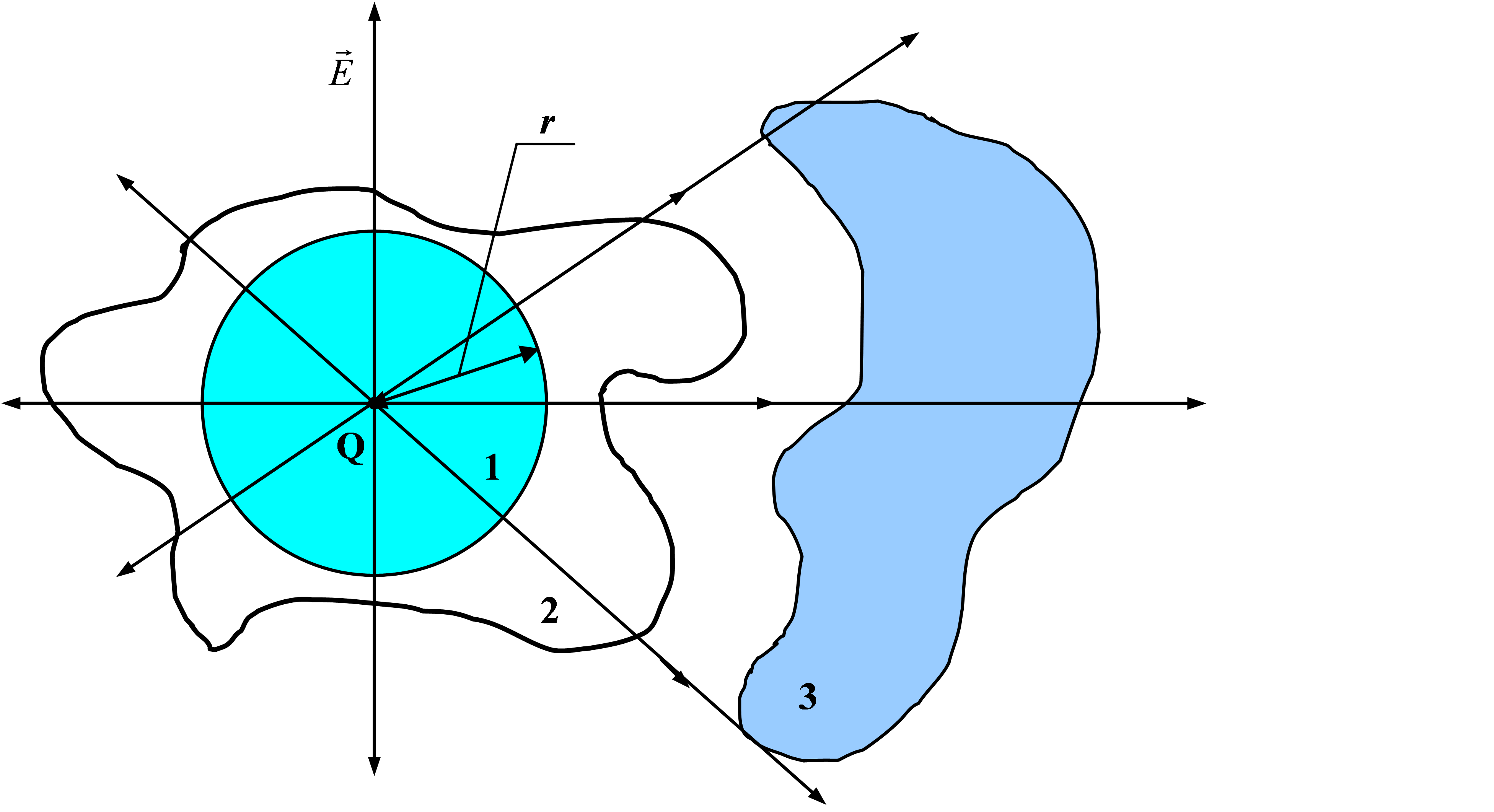
Учитывая последнее замечание, запишем поток (2.7) в следующем виде:

Таким образом, для первого простейшего случая теорема Гаусса оказалась справедливой. Что из этого следует?

Полученный результат позволяет заключить, что найденный поток не зависит от радиуса гауссовой поверхности. Это легко понять: ведь с увеличением расстояния от заряда Q площадь поверхности растёт пропорционально квадрату радиуса, а напряжённость поля убывает обратно пропорционально квадрату радиуса.

Вспомним, кроме того, что поток вектора напряжённости равен числу силовых линий, пронизывающих гауссову поверхность. Независимость потока от радиуса поверхности означает, что силовые линии поля точечного заряда, начинаясь на положительном заряде, простираются далее до бесконечности, не прерываясь. Отсюда - дальнейшие выводы.

Поток вектора напряжённости поля точечного заряда через любую замкнутую поверхность (рис. 2.5, 2), охватывающую точечный заряд Q , равен отношению

Этот вывод несомненен, так как поток равен прежнему неизменному числу силовых линий, пронизывающий замкнутую поверхность.

Поток вектора напряжённости, через произвольную замкнутую поверхность, не охватывающую электрический заряд, равен нулю (рис. 2.5, 3).

Этот вывод также легко понять, так как число силовых линий втекающих в гауссову поверхность, равно числу линий, покидающих её. Поэтому суммарный поток через эту поверхность равен нулю.

Теперь можно обратиться к рассмотрению общего случая: пусть произвольная замкнутая поверхность S охватывает N точечных зарядов (рис. 2.6.). Вычислим поток вектора напряжённости суммарного поля через эту поверхность S, учтя, что в соответствии с принципом суперпозиции результирующее поле равно векторной сумме отдельных полей

Итак, воспользовавшись определением потока, вычислим его через произвольную замкнутую поверхность S .

(2.9)

Полученный результат является доказательством справедливости теоремы Гаусса: поток вектора напряжённости электростатического поля в вакууме через любую замкнутую поверхность пропорционален алгебраической сумме зарядов, заключенных внутри этой поверхности .