Svojstva fizičkih tijela i objekata OPI fizičke količine . Jedna od tih količina za električno polje je tenzija. U skladu s prethodno definiranom definicijom, on opisuje akciju napajanja polja na zore-ženska tijela na određenoj tački električnog polja. Ako je polje nehomogeno, tada je napetost na različitim točkama polja drugačija. I da bi se opisala svojstva polja u mnogim bodovima, potrebno je dostaviti veliki broj vrijednosti napetosti. Ovo mora borci proučavati polje i sprječava stvaranje prezentacije osobe u svakom konkretnom slučaju u mašti.

Snaga električnog polja su njegove karakteristike snage.

Bolje je predstavljati strukturu električnog polja pomoći grafička metoda. Na temelju grafičkog načina zastupanja električne konstrukcije Postoje preispitati pojave koji se mogu primijetiti u eksperimentima.

Neka b električno polje Lopta sa pozitivnim nabijenim ima malu česticu neke tvari, takođe ima polo. Ako je ova djelomična besplatna, a radnja gravitacijskog polja nije značajna, tada će pod utjecajem električne energije kretati se iz lopte. To će se posmatrati bilo gdje u polju napunjene kugle (Sl. 4.20).

Predstavljajući putanju kretanja mnogih pozitivno nabijenih čestica, koji se nalazi u električnom polju i pokazuje im smjer trenutne sile, nazvana polu-chim spektar Ovo polje.

Nazivaju se linije koje čine spektar električnog polja linije napetostielektrično polje ili tihe linije.

Koncept linija sile Prvi put uveden u nauku M. Faraday na osnovu znanja dobivenih tokom eksperimentalnih pregleda.

Eksperimenti, poznati M. Faraday, mogu se implementirati u savremenim uvjetima.

Uzmite metalni vodič sa papirnim trakom pričvršćenim na njega i povežite ga s dirigenticom elektrofore uređaja. Ako ga prepustimo, svi trake od papira razlikuju se u različitim smjerovima kao rezultat uzajamnog od PIN-a (Sl. 4.21). Rezultati ovog iskustva (i slično) omogućavaju post-znamenku električnog polja zasebnog nabijenog tijela. Prikazuje se na slici. 4.22. Strelice na dalekovodu prikazane su smjer sile koji će djelovati na pozitivno nabijeno tijelo koje se nalazi u ovom trenutku.

Stoga, dalekovode "izlažu" iz pozitivnog nabijenog tijela i "ulaze" u negativno nabijeno tijelo (Sl. 4.22). Istovremeno treba pamtiti da su "iscrpili" i "ulaze" okomito na površinu tijela.

Linije električnog intenziteta su okomito na površinu napunjenog tijela na tim tačkima u kojima počinju. Materijal sa stranice.

Uzmite dva metalna dirigenta sa trakama za papir i povežite ih s provodnikom elektrofore uređaja. U to vrijeme elektrolitni stroj i vidimo da će trake za papir početi jedno prema drugoj (Sl. 4.23). Prema dva raznovrsno naplaćena tijela, polje dva različita nabijena tijela imat će spektar prikazan na slici. 4.24.

Curvilinear oblik napetosti zbog činjenice da postoje dvije sile od svakog tijela sa strane svakog tijela. Okovanje ovih snaga na svakoj tački polja je tangenta za crte napetosti.

Tangenti linije na koje u bilo kojem trenutku pokazuju smjer sile koji djeluje na pozitivno nabijeno tijelo koje se zove životni vijek.

Smjerovi sila koje će biti važeće na različitim tačkima polja dvaju prašine-ženskih tijela prikazane su na slici. 4.25.

Budući da su napetosti uvijek okomito na površinu, spektar tjelesnih polja različitih oblika bit će različiti (Sl. 4.26).

Na ovoj stranici materijal na temama:

• Spectra e-pošte. polja raznih nabijenih tijela

• Grafička slika električnog polja Sažetak

• Slike linija električnih polja na eksperimente

• Za veću jasnoću, električno polje je često prikazano korištenjem dalekovoda i ekvipotencijalnih površina.

  Dalekovodi – ovo su kontinuirane tangente za koje se na svakom trenutku prolaze, podudaraju se sa vektorom snage električnog polja (Sl. 1.5). Debljina dalekovoda (broj dalekovoda koji prolaze kroz površinu jedinice) proporcionalan je snazi \u200b\u200belektrične polje.

  Equipotencijalne površine (ekvivalencijalna) – površine jednakog potencijala. Ovo su površine (linije), pri vožnji na kojoj se potencijal ne mijenja. Inače, potencijalna razlika između dvije bilo koje tačke ekvipotencijalne površine je nula. Dalekovodi Okomito na ekvipotencijalne površine i usmjereni su prema najoštrije pad potencijala. Ova činjenica slijedi iz jednadžbe (1.10) i dokazuje se tokom matematičke analize po odjeljku "Scalarna i vektorska polja".

  Razmotrite električno polje stvoreno na daljini 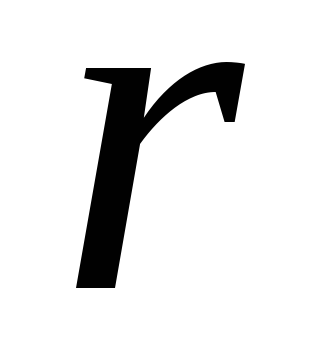od točke naboja. Prema (1.11, b) vektor zatezanja poklapa se sa smjerom vektora Ako je naboj pozitivan, a suprotna mu ako je naboj negativan. Shodno tome, dalekovodne snage se radijalno preusmjere od punjenja (Sl. 1.6, A, B). Debljina dalekovoda, kao i napetosti, obrnuto proporcionalno na kvadrat udaljenosti (
  
  ) Prije naplate. Equipotencijalne površine električnog polja po mirnim nabojem su sfere sa sredinom na lokaciji punjenja.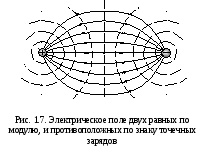

  

  

  Na slici. 1.7 prikazuje električno polje sustava dva jednaka u modulu, ali suprotno znaku troškova bodova. Omogućujemo da sami učinimo ovim primjerom. Imamo samo samo da snage moći uvijek počinju na pozitivnim nabojima i završava na negativnu. U slučaju električnog polja od jedne tačke (Sl. 1.6, A, B) pretpostavlja se da su dalekovodi na vrlo daljinskim nabojima suprotnog znaka. Vjeruje se da je svemir uglavnom neutralan. Stoga, ako postoji optužbi za jedan znak, onda negdje ja ću definitivno imati jednako u modulu optužbe drugog znaka.

  1.6. Gaussova teorema za električno polje u vakuumu

  Glavni zadatak elektrostatike je zadatak pronalaska napetosti i potencijala električnog polja na svakoj tački prostora. U stavku 1.4, odlučili smo zadatak polja poantanj optužbe i također razmotriti polje sustava tačke optužbi. U ovom će se stavku biti o teoremi koja vam omogućuje izračunavanje električnog polja složenijih nabijenih predmeta. Na primjer, nabijen dugačak nit (ravan), napunjeni avion, napunjena sfera i drugi. Izračunavanje snage električnog polja na svakoj tački prostora pomoću jednadžbi (1,12) i (1.13), moguće je izračunati potencijal na svakoj tački ili potencijalnu razliku između dva bilo koje tačke, I.E. Riješite glavni zadatak elektrostatike.

  Za matematički opis uvodimo koncept struje napetosti ili struju električnog polja. Stream (f) vektor električno polje kroz ravnu površinu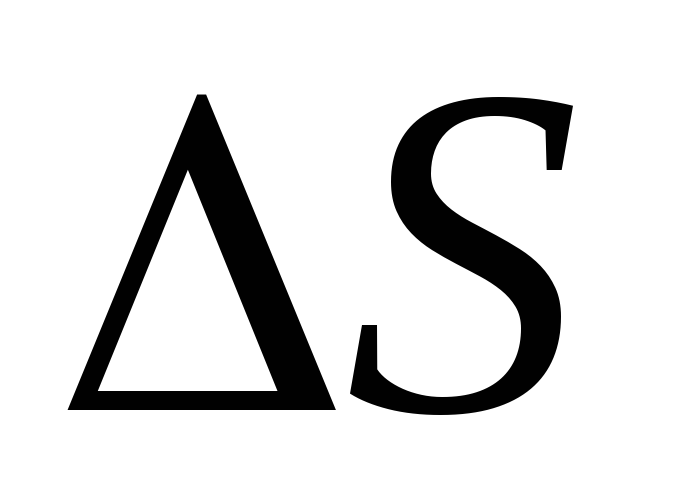
  
  nazvana vrijednost:

  
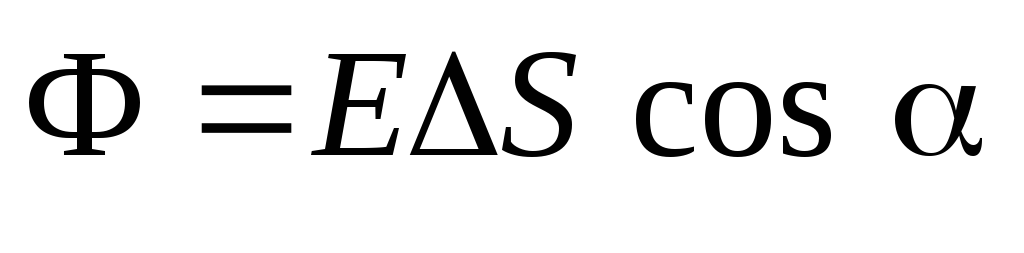  , (1.16)

  

  gde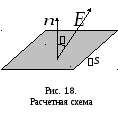 - Snaga električnog polja, koja se očekuje da će konstantno u okviru objekta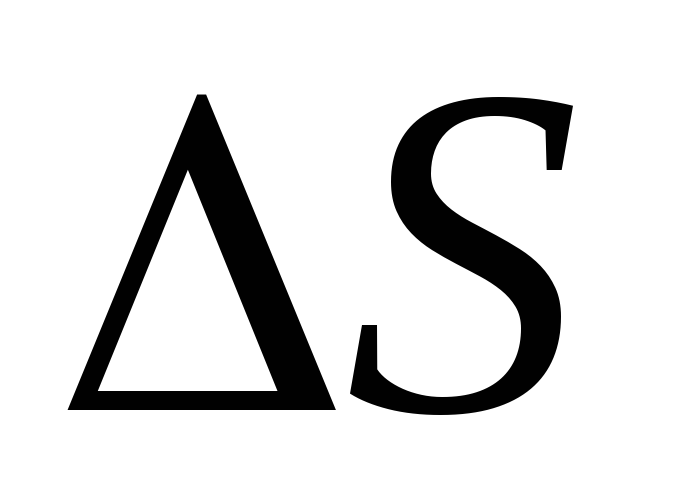
  
  ;
  
  - ugao između smjera vektora i pojedinačni vektor normalan 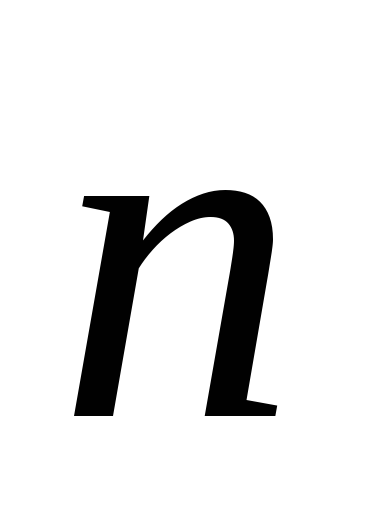do stranice
  
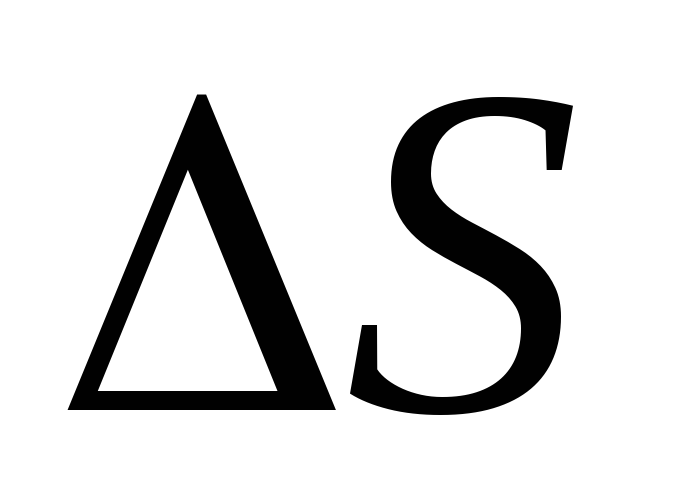  (Sl. 1.8). Formula (1.16) može se snimiti pomoću koncepta skalarnog proizvoda vektora:

  
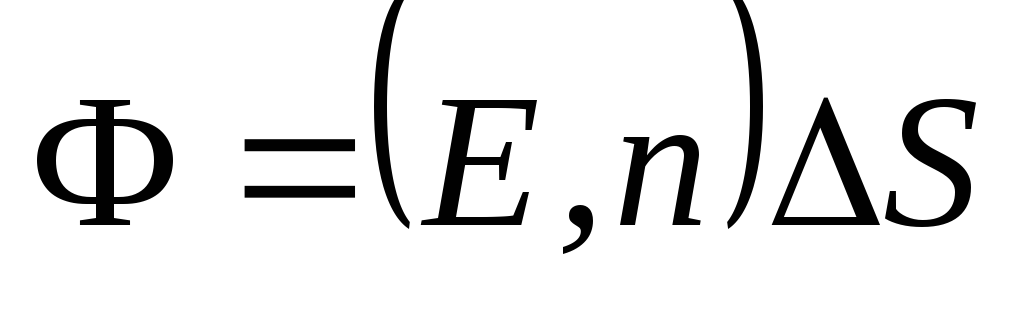  . (1.15, a)

  U slučaju kada je površina nije ravan, mora se podijeliti u male dijelove za izračun potoka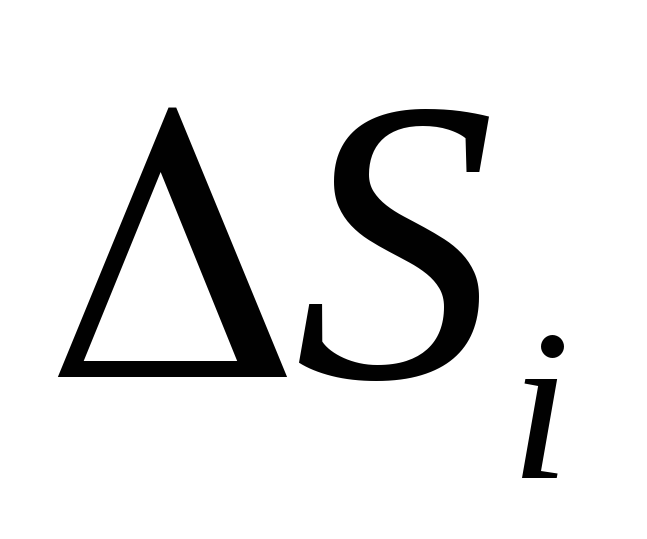
  
  Što se može otprilike smatra ravnim, a zatim zapisati izraz (1,16) ili (1,16, a) za svaki komad površine i preklopiti ih. U granici kada je površina S. i. vrlo male
  
  ), takav iznos se naziva površinski integral i označava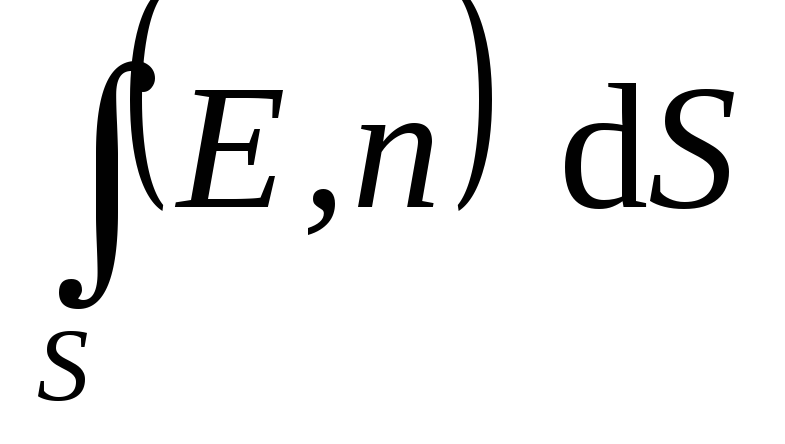
  
  . Dakle, protok vektora čvrstoće električnog polja kroz proizvoljnu površinu određeno izrazom:

  
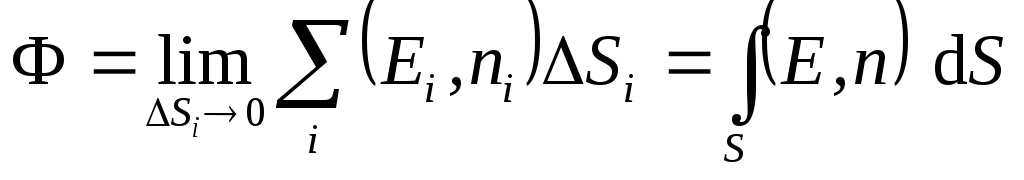  . (1.17)

  Kao primjer, razmislite o sferi radijusa 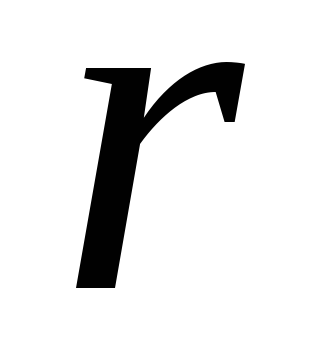, koji je centar od kojih je pozitivna tačka naboja I mi definiramo protok električnog polja kroz površinu ove sfere. Power linije (vidi, na primjer, Sl.1.6, a) Izlazi iz naplate, okomito na površinu sfere, a na svakoj tački sfere modul čvrstoće polja je isti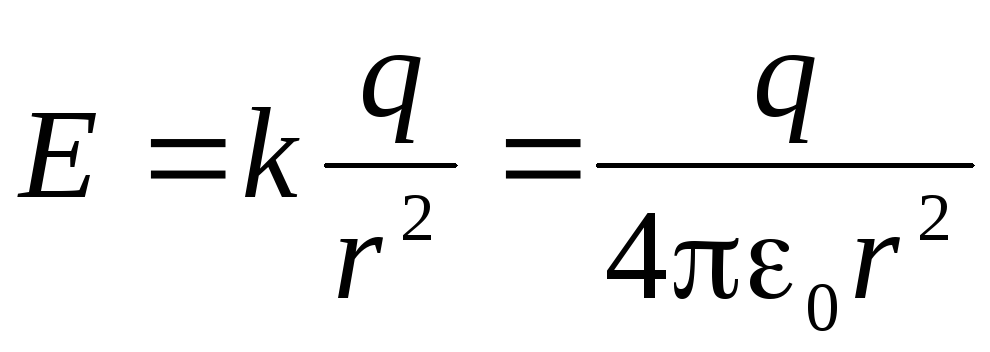

  
  .

  Kvadratna sfera
  
  ,

  onda
  
  
  
  
  
  .

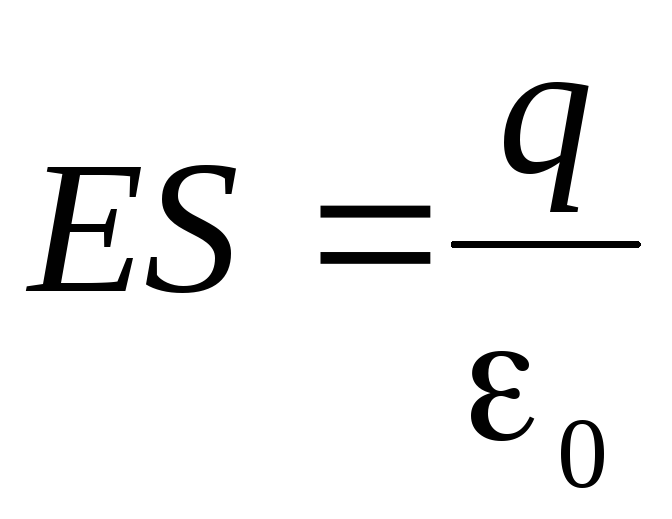  Vrijednost
  
  i to je protok električnog polja kroz površinu sfere. Tako imamo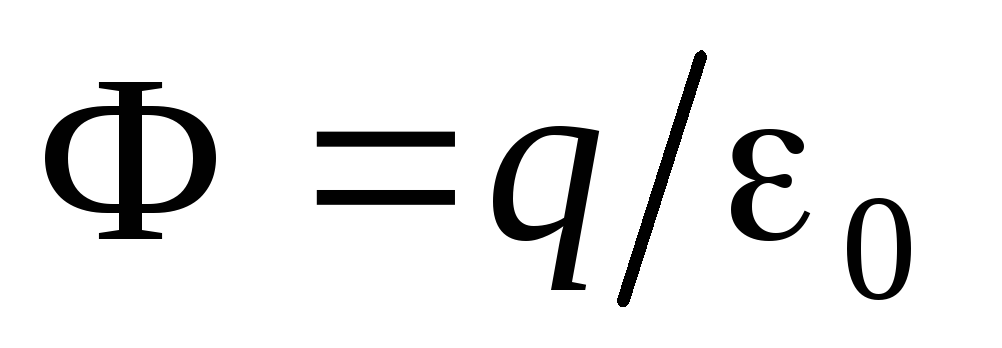
  
  . Može se vidjeti da protok kroz površinu sfere električnog polja ne ovisi o radijusu sfere, a ovisi samo o samoj optužbi . Stoga, ako držite niz koncentričnih sfera, protok električnog polja kroz sva ova područja bit će ista. Očito je da će i broj dalekovoda koji preći ove sfere također biti isti. Broj dalekovoda koji su izlaze izvan terena, uzimajući jednak tok električnog polja:
  
  .

  Ako se sfera zamijeni bilo kojom drugom zatvorenom površinom, a zatim protok električnog polja i broja dalekovoda koji prelaze. Pored toga, protok električnog polja kroz zatvorenu površinu i stoga je broj dalekovoda koji prodiru u ovu površinu jednak
  
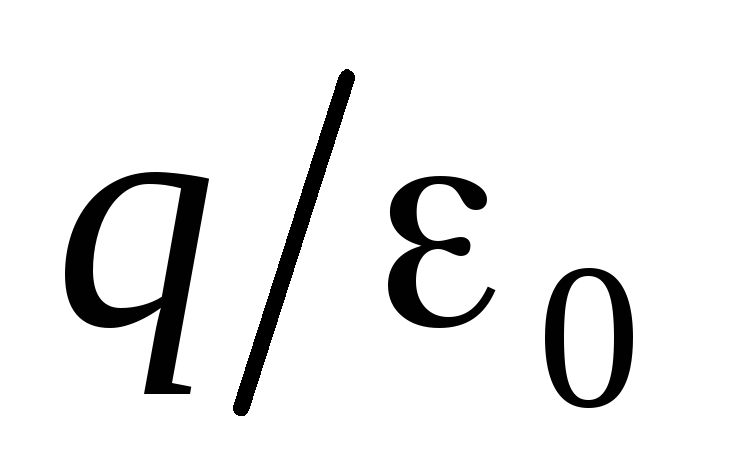  ne samo za točku točke naboja, već i za polje stvoreno bilo kojom kombinacijom tačke optužbi, posebno, nabijenog tijela. Tada veličine treba se smatrati algebričnom količinom cjelokupne ukupnosti optužbi unutar zatvorene površine. Ovo je suština Gauss Teorem, koja je formulisana na sljedeći način:

  VECTOR VECTOR ELEKTRIČNOG PODRUČJA kroz proizvoljnuzatvoren površina je jednaka
  
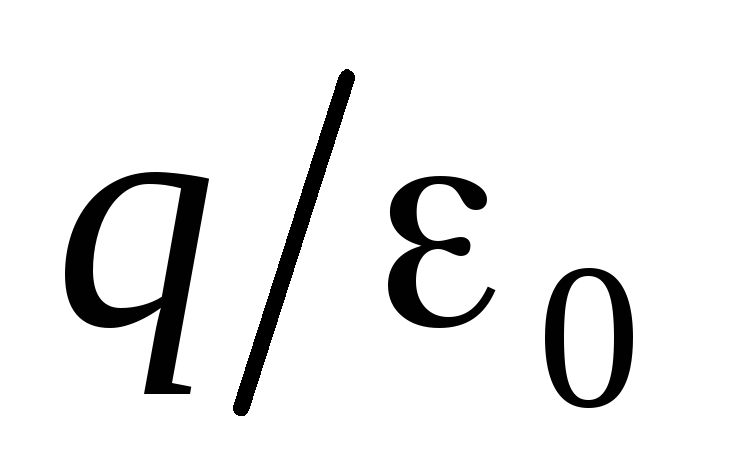  gde
  
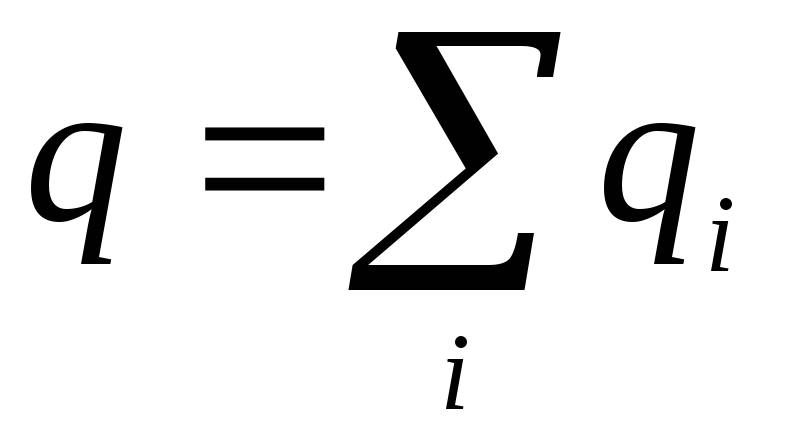
   algebraic Zaključena količina troškovaiznutra ova površina.

  Matematički teorema može biti napisana kao

  
  . (1.18)

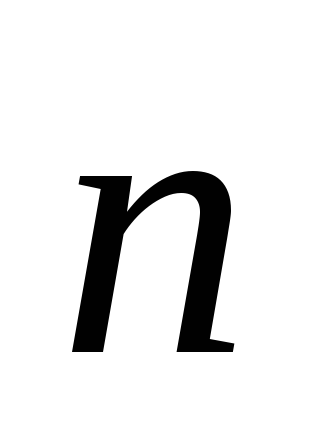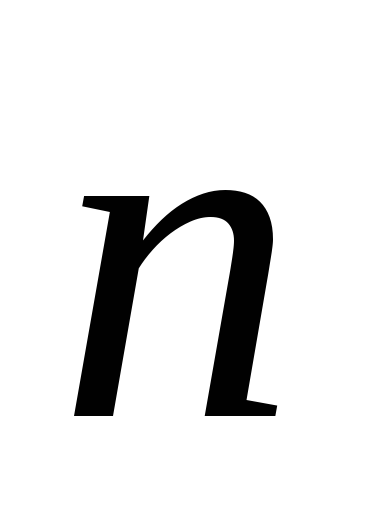  Imajte na umu da ako na nekoj površini S. vektor trajni i paralelni vektor , a zatim protok kroz takvu površinu. Pretvaranje prvog integralnog, prvo smo koristili činjenicu da vektori i paralelno, što znači
  
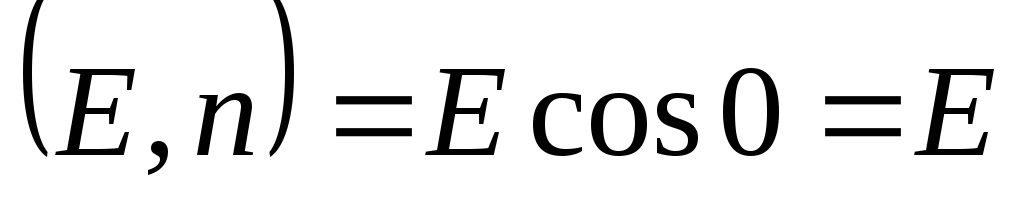  . Zatim su isporučili iznos za znak integralnog zbog činjenice da je konstantno bilo gdje u sferi . Koristeći Gausson Theorem za rješavanje određenih zadataka, pokušava odabrati površinu za koju gore opisani uvjeti pokušavaju posebno kao proizvoljna zatvorena površina.

  Dajemo nekoliko primjera za primjenu Gauss Theorem.

  Primjer 1.2.Izračunajte snagu električnog polja ravnomjernog nabijenog beskrajne niti. Odredite potencijalnu razliku između dvije tačke u takvom polju.

  Odluka. Pretpostavimo sigurno da se nit naplaćuje pozitivno. Simetrijom zadatka može se tvrditi da će dalekovodne snage biti radijalno divergen iz osi navoja ravno (Sl.1.9), čija je gustoća smanjena iz niti u nekom zakonu. Veličina električnog polja smanjit će se po istom zakonu. 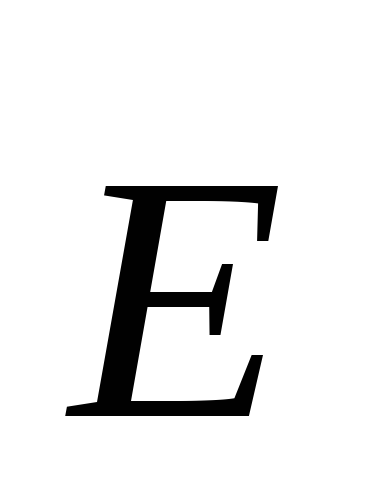. Equipotencijalne površine bit će cilindrične površine s osi koja se podudara sa nitima.

  Neka jedinica naboja duljine teme jednaka . Ova se vrijednost naziva linearnom gustoćom punjenja i mjeri se u SI u jedinicama [CL / M]. Da biste izračunali snagu polja, primijenite gauss teorem. Da biste to učinili, kao proizvoljna zatvorena površina odaberite radijusni cilindar 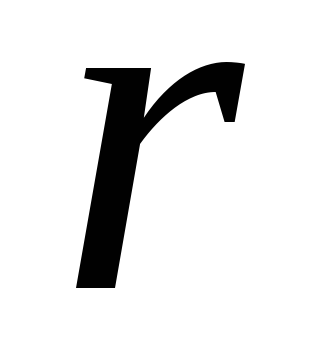i dužina 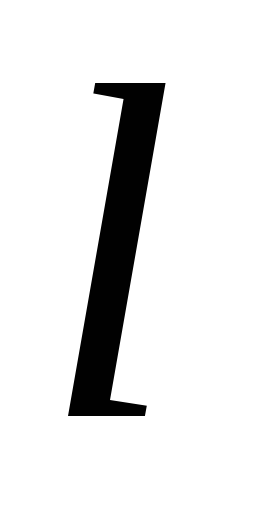Čija se osovina poklapa sa niti (slika.1.9). Izračunajte protok električnog polja kroz površinu cilindra. Puni potok sastoji se od potoka kroz bočnu površinu cilindra i protoka kroz bazu

  Ali,
  
  jer u bilo kojem trenutku na bazu cilindra
  
  . To znači da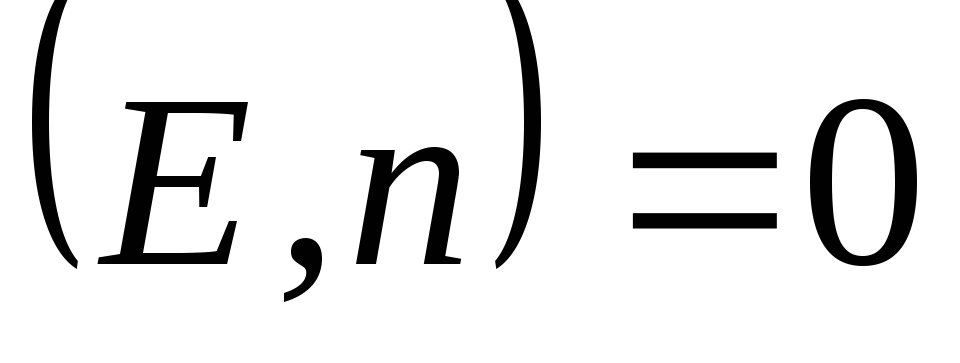
  
  na tim tačkama. Potok kroz bočnu površinu
  
  . Prema Theorem Gaussu, ovaj kompletan protok je jednak
  
  . Tako je dobio

  
  .

  Količina troškova unutar cilindra, izražava se linearnom gustoćom naboja :
  
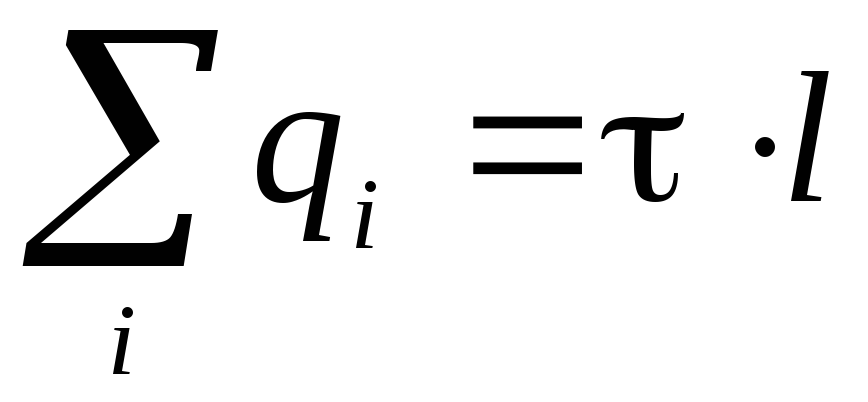  . S obzirom na to
  
  , dobiti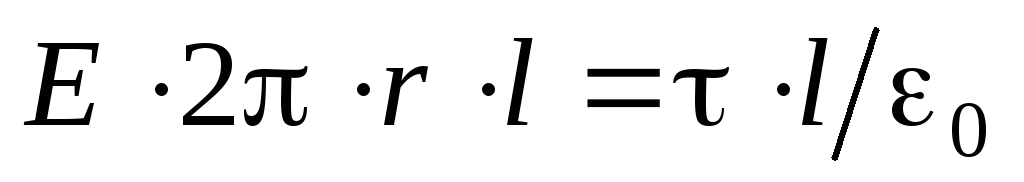

  
  ,

  
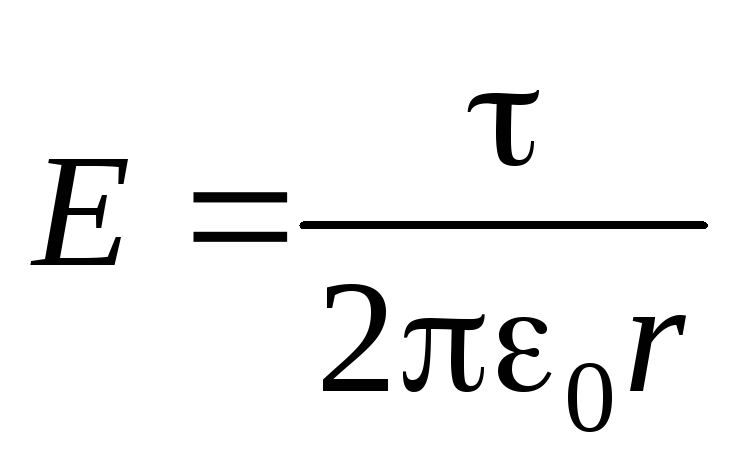  , (1.19)

  oni. Napetost i gustina dalekovoda električnog polja jednolično nabijenog beskrajnog niti smanjuju se obrnuto proporcionalno u daljinu (
  
  ).

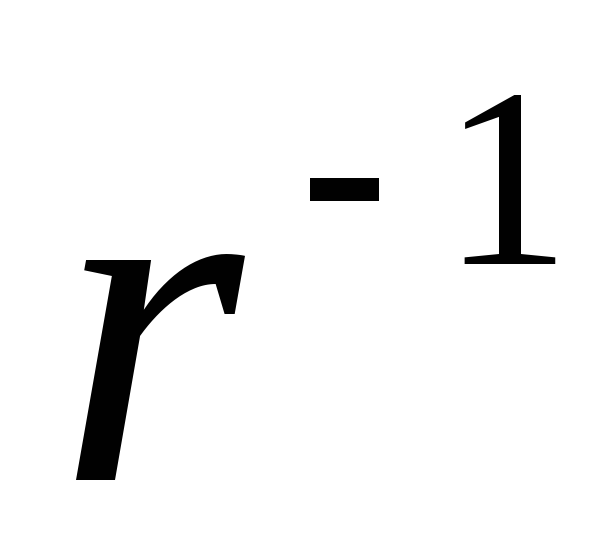  Pronađite potencijalnu razliku između bodova koji se nalaze na udaljenostima 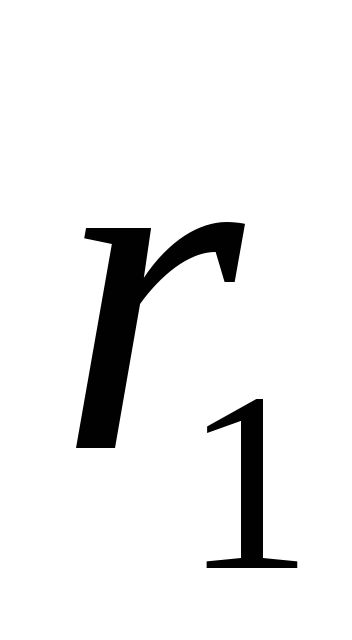i 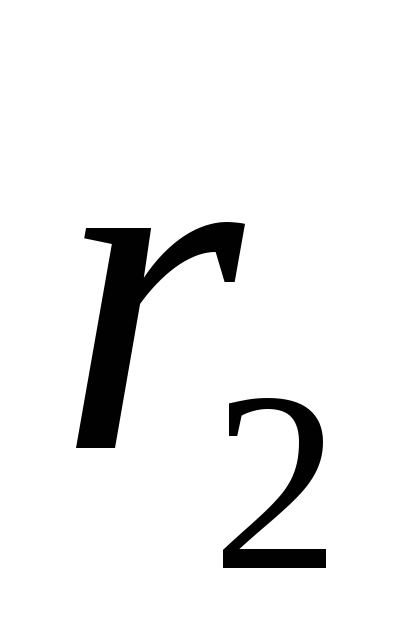iz niti (u vlasništvu ekvipotencijalnih cilindričnih površina sa radijusom 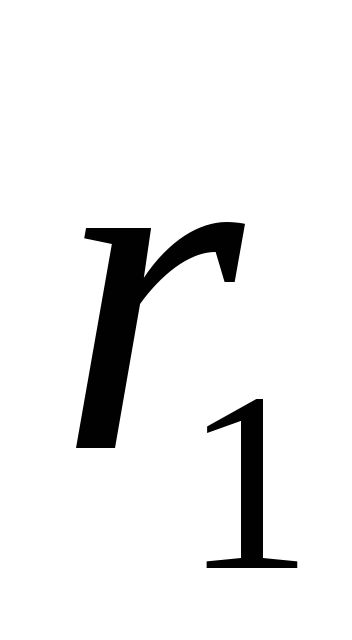i 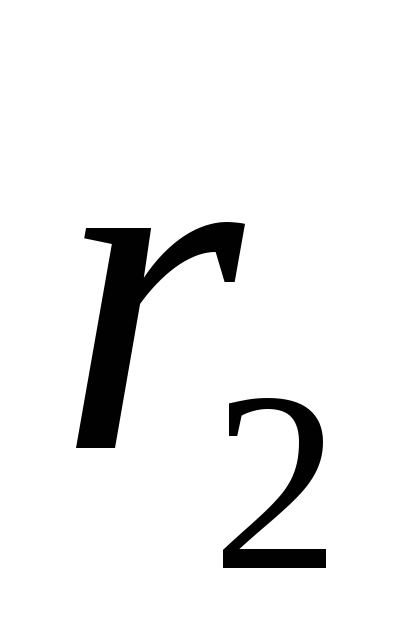). Da biste to učinili, koristimo napetost električnog polja s potencijalom u obliku (1,9, b):
  
  . S obzirom na izraz (1.19), dobivamo diferencijalnu jednadžbu sa odvajanjem varijabli:

  
  
  
  
  
  
  
  

  
  
  
  
  
  .

  

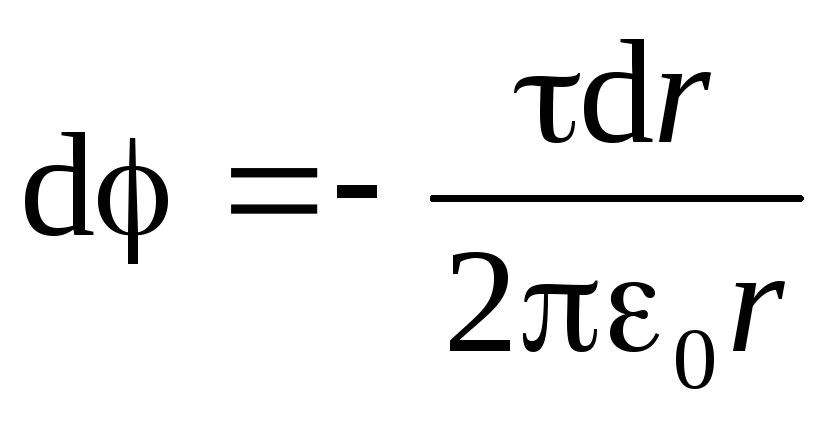
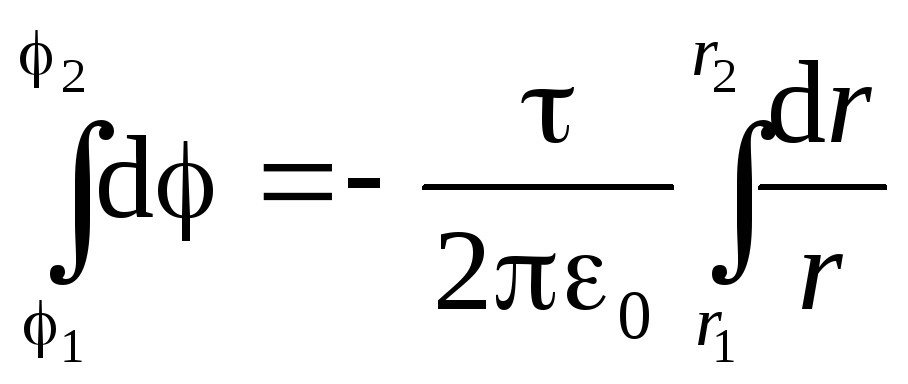
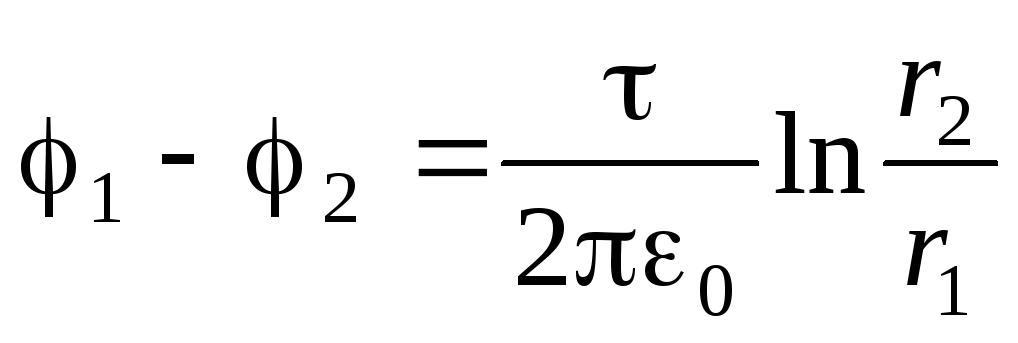  Primjer 1.3.Izračunajte snagu električnog polja ravnomjernog napunjenog aviona. Odredite potencijalnu razliku između dvije tačke u takvom polju.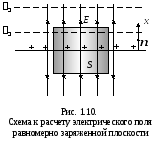

  Odluka. Električno polje jednolično napunjenog aviona prikazano je na slici. 1.10. Na vrlini simetrije, dalekovodne snage moraju biti okomito u avion. Stoga može odmah zaključiti da debljina linija, a, prema tome, napetost električnog polja prilikom uklanjanja aviona neće se mijenjati. Equipotencijalne površine su avioni paralelno s ovim napunjenim ravninom. Pretpostavimo da je jedinica za punjenje aviona jednaka . Ova se vrijednost naziva površinska gustoća punjenja i mjeri se u C u jedinicama [CL / M 2].

  Primijenite Gauss Theorem. Da biste to učinili, kao proizvoljna zatvorena površina odaberite dužinu cilindra 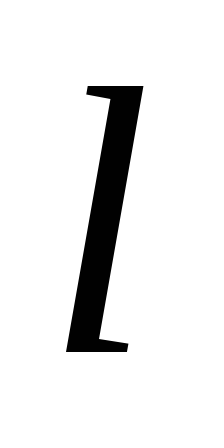, čija je osovina okomita u ravninu, a baze su ravnoteže od nje (Sl.1.10). Ukupno struja električnog polja
  
  . Protok kroz bočnu površinu je nula. Protok kroz svakoj bazi jednaki je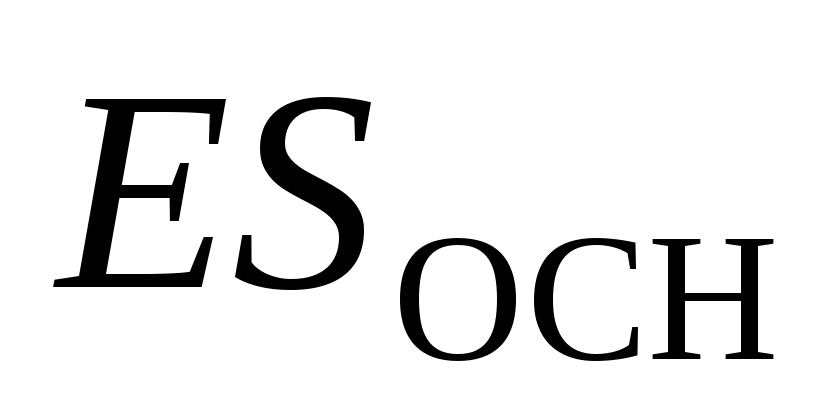
  
  , pa tako
  
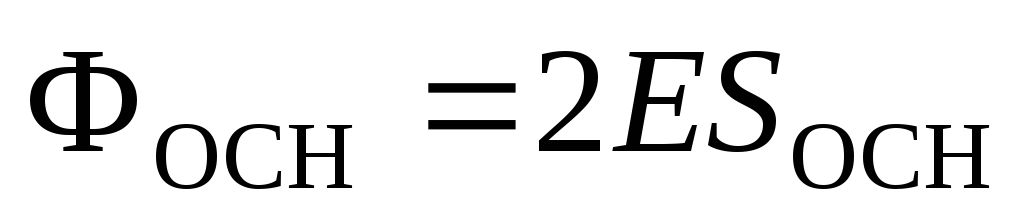  . Prema Gaussovoj teoreme, dobivamo:

  
  .

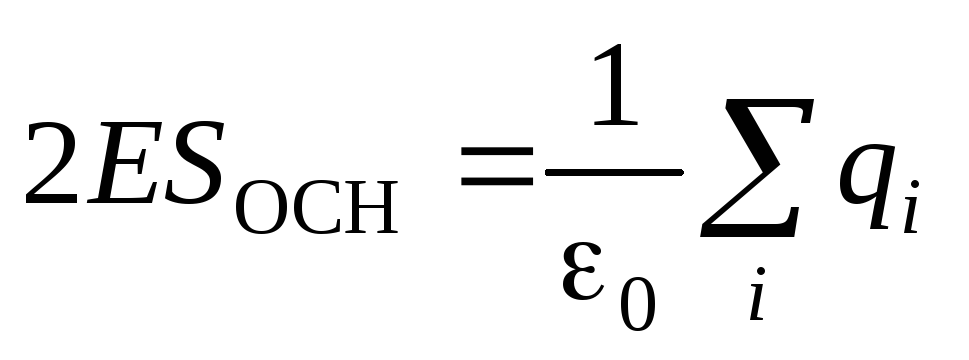  Zbroj optužbi unutar cilindra Otkrićemo kroz površnost gustoće optužbe :
  
  . Zatim, lokacija:

  
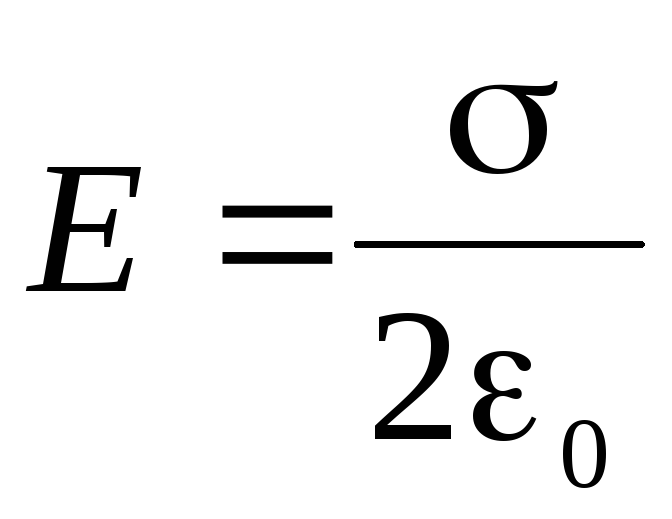  . (1.20)

  Iz rezultirajuće formule može se vidjeti da intenzitet oblasti uniformnog napunjenog aviona ne ovisi o udaljenosti do nabijenog aviona, I.E. U bilo kojem prostoru (u jednoj polovini) je isti i modul, a u smjeru. Ovo polje se zove uniform. Dalekovodi jednoliko polje Paralelno, njihova gustina se ne mijenja.

  Pronađite potencijalnu razliku između dvije tačke homogenog polja (u vlasništvu ekvipotencijalnih aviona i Ležajući u jednom polu-ravninu u odnosu na napunjenu ravninu (Sl.1.10)). Usmjeravamo osovinu 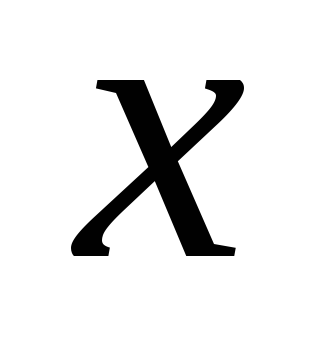vertikalno prema gore, tada je projekcija vektora zatezacije na ovoj osi jednak modulu vektora zatezanje
  
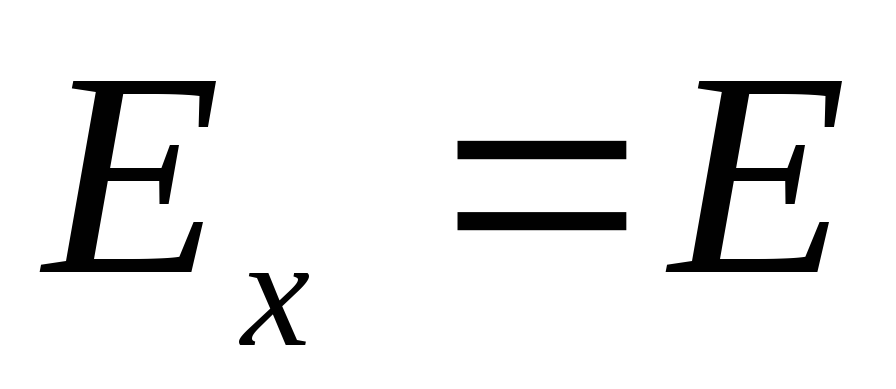  . Koristimo jednadžbu (1.9):

  
  
  
  
  
  
  
  
  
  
  
  
  
  .

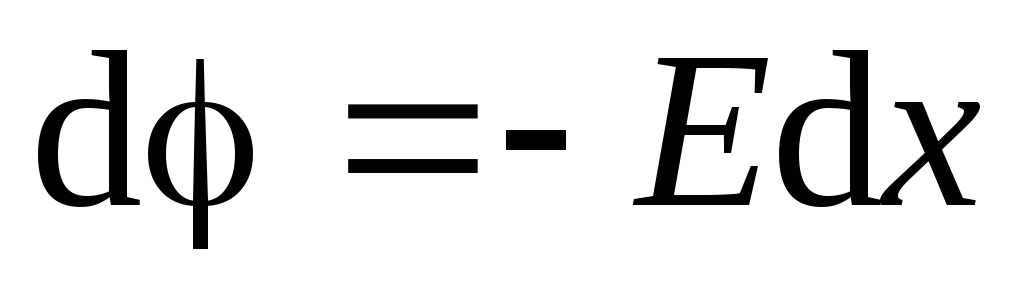
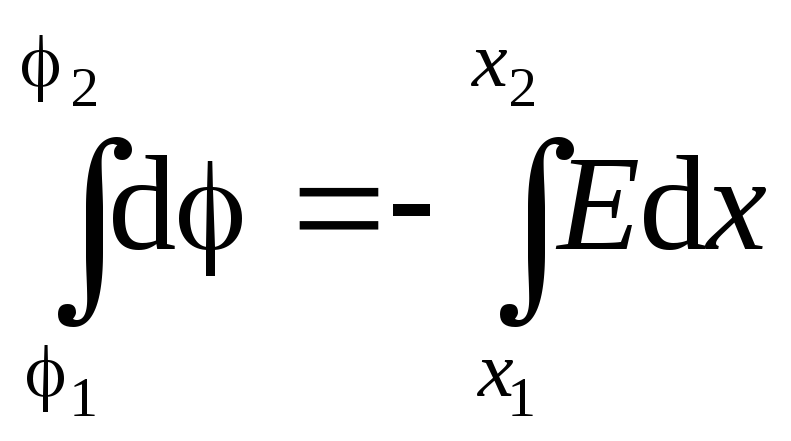  Trajna količina (Jednolično) može se izvesti iz integralnog znaka: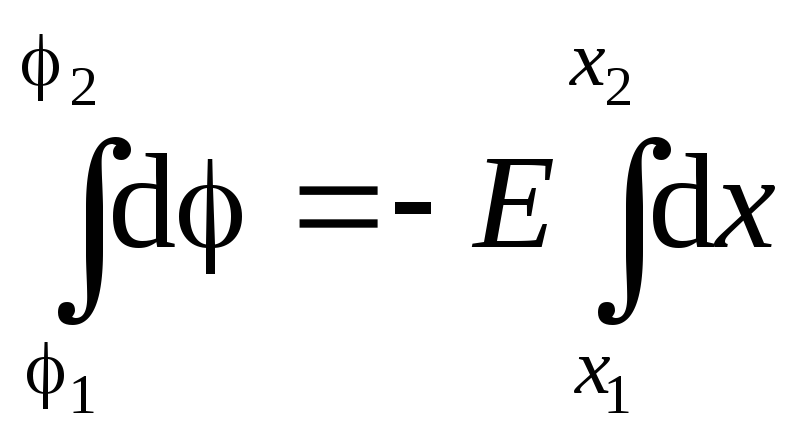
  
  . Integriranje, dobivamo:. Dakle, potencijal homogenog polja linearno ovisi o koordinati.

  Razlika potencijala između dvije točke električnog polja - postoji napon između tih tačaka ( ). Označavaju udaljenost između ekvipotencijalnih aviona
  
  . Tada se može napisati da u jednoličnom električnom polju:

  
  . (1.21)

  Još jednom naglašavamo da kada koristite Formulu (1.21) morate se sjetiti da vrijednost  Ne udaljenost između točaka 1 i 2, a udaljenost između ekvipotencijalnih aviona, koje ovi točke pripadaju.

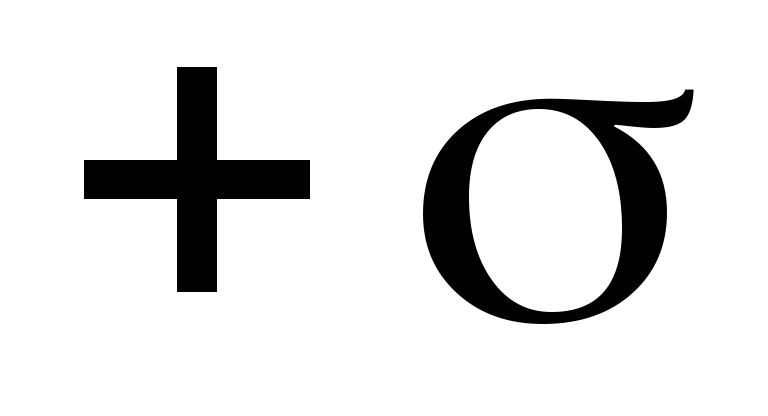  Primjer 1.4.Izračunajte snagu električnih polja dva paralelna aviona, jednolično napunjena površinskim gustoćom optužbi
  
  i
  
  .

  Odluka. Koristimo rezultat primjera 1.3 i princip superpozicije. Prema ovom principu, rezultirajuće električno polje u bilo kojoj točki prostora
  
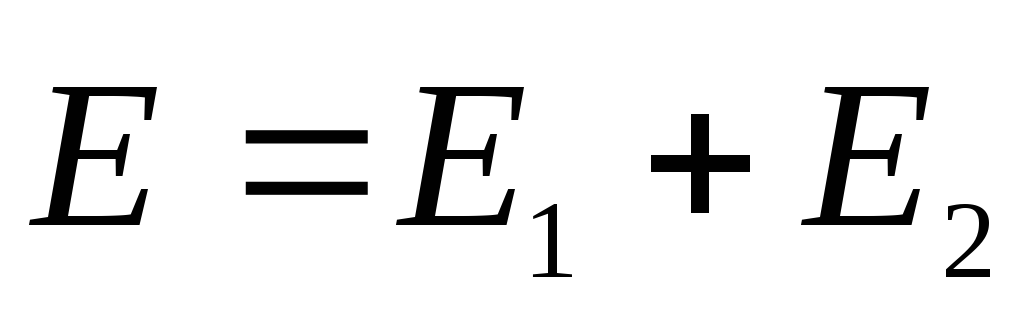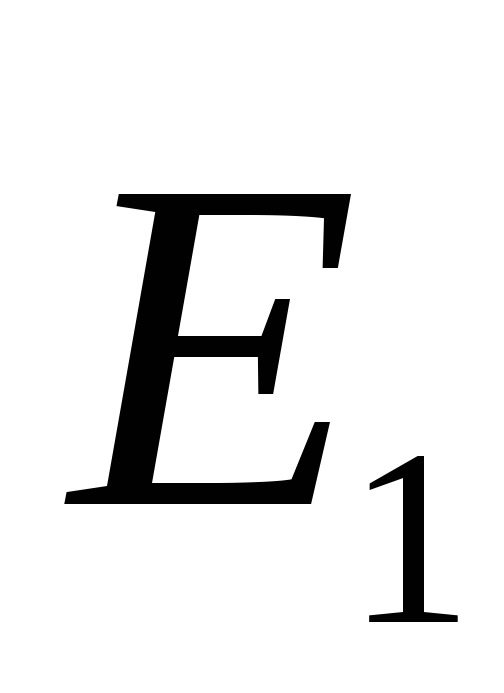  gde i 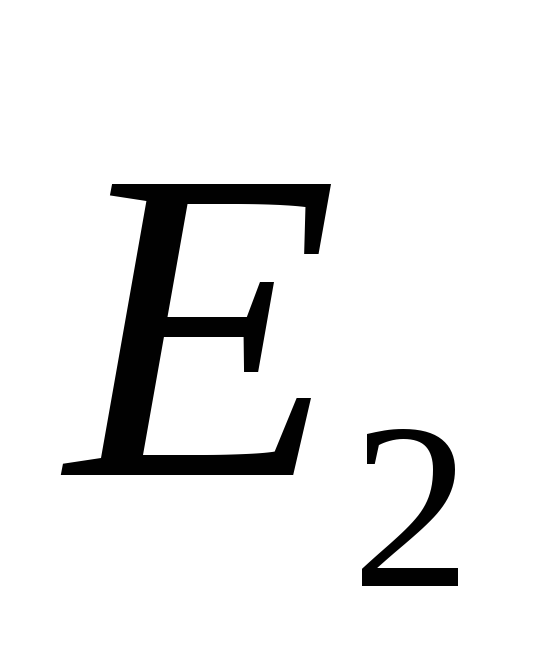- Električna polja prve i druge ravnine. U prostoru između vezona vektora 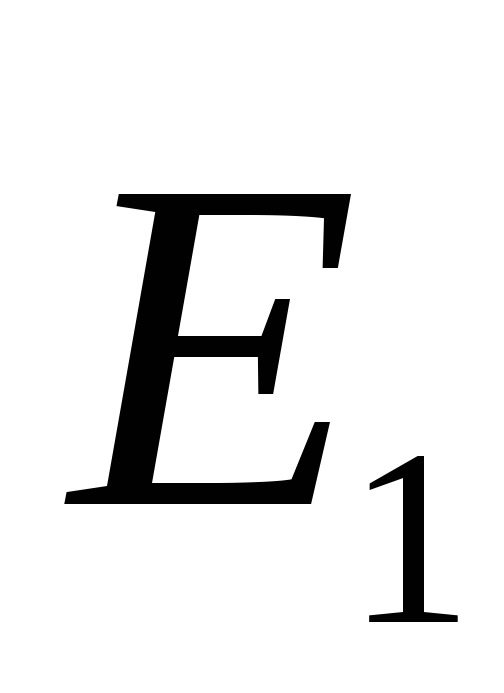i 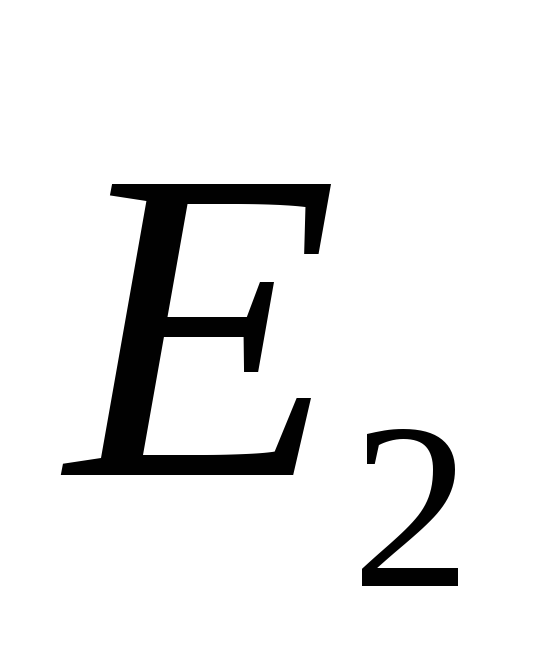usmjeren u jednom smjeru, tako da referentni modul čvrstoće polja. U vektoru vanjskog prostora 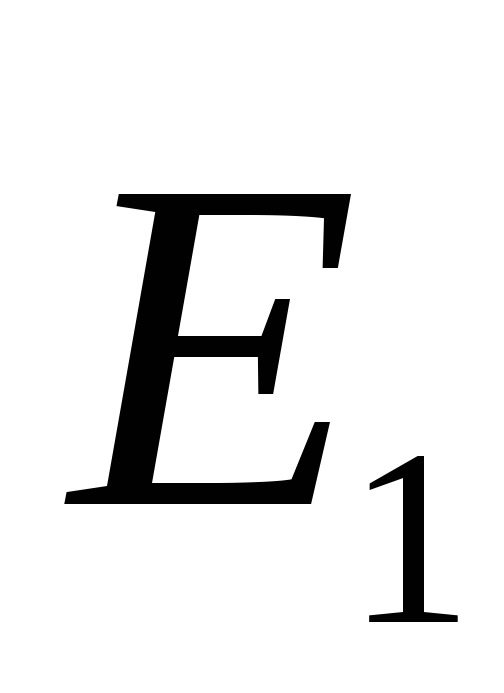i 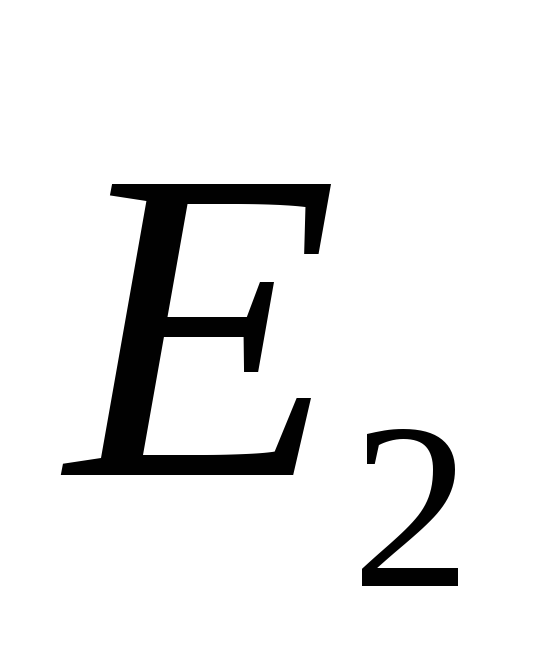usmjeren u različite smjerove, dakle (Sl. 1.11). Dakle, električno polje je samo u prostoru između aviona. To je homogeno, jer je to zbroj dva homogena polja.

  Primjer 1.5. Pronađite napetost i potencijal električnog polja jednolično napunjene sfere. Ukupna naknada sfera jednaka je , a radijus sfere - .

  Odluka. Zbog simetricije raspodjele naboja, dalekovode bi trebale biti usmjerene u radijci sfere.

  Razmislite o području unutar sfere. Kao proizvoljna površina odaberite sferu radijusa
  
  , čiji se centar podudara sa središtem nabijene sfere. Zatim protok električnog polja kroz sferu S.:
  
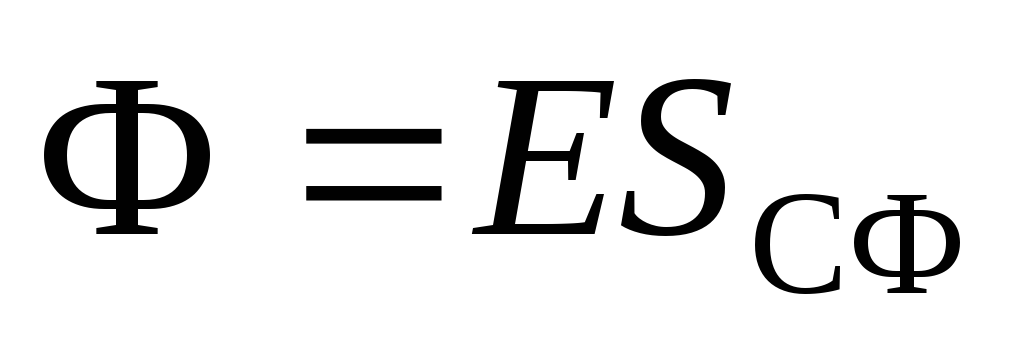  . Iznos troškova unutar sfere polumjer 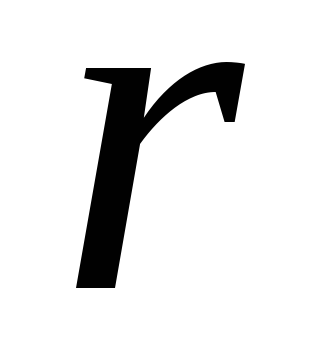jednak nuli, jer se svi optužbe nalaze na površini radijus sfere
  
  . Zatim na Theorem Gaussu: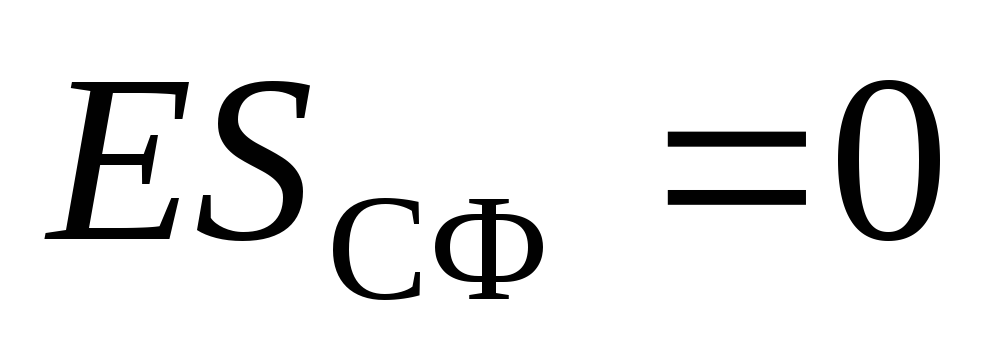
  
  . Ukoliko
  
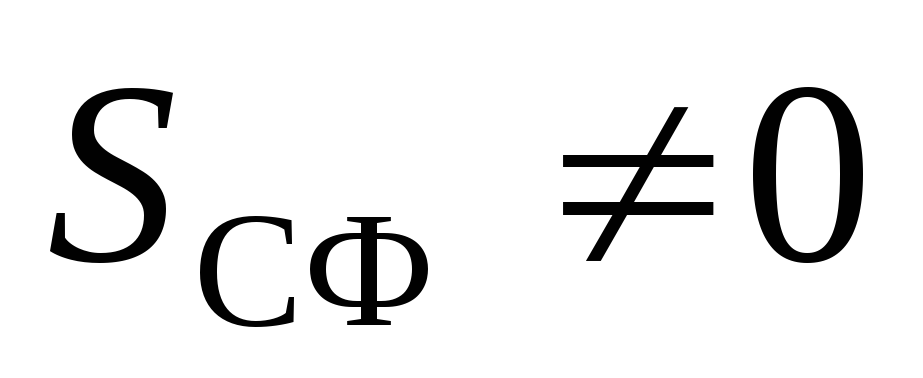  T.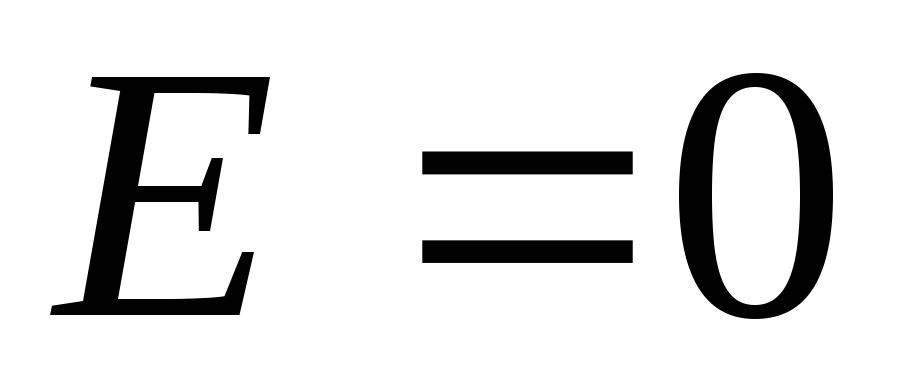
  
  . Dakle, unutar jednolično napunjenog polja polja.

  Razmislite o području izvan sfere. Kao proizvoljna površina odaberite sferu radijusa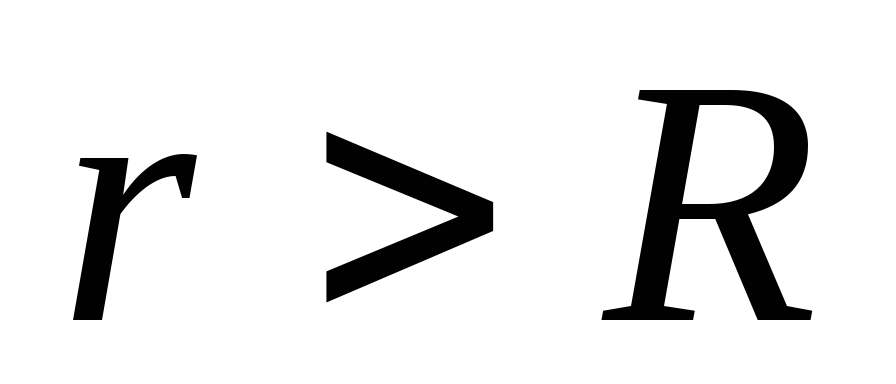
  
  , čiji se centar podudara sa središtem nabijene sfere. Struja električnog polja kroz sferu :
  
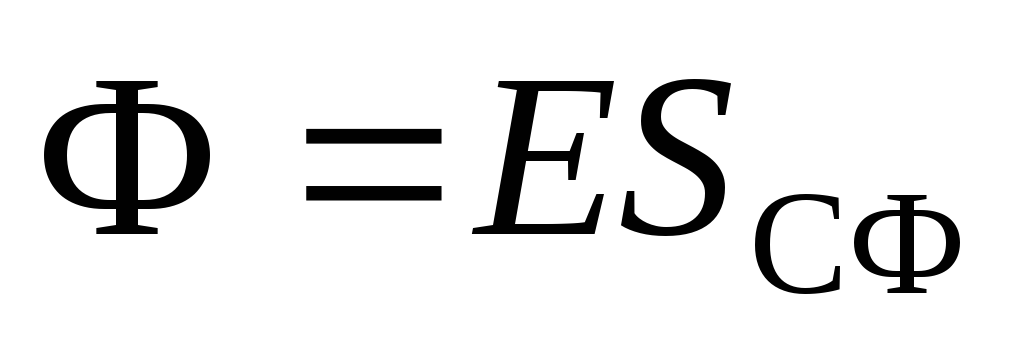  . Iznos troškova unutar sfere jednaka je punom naboju naplata polumjerna sfera . Zatim na Theorem Gaussu: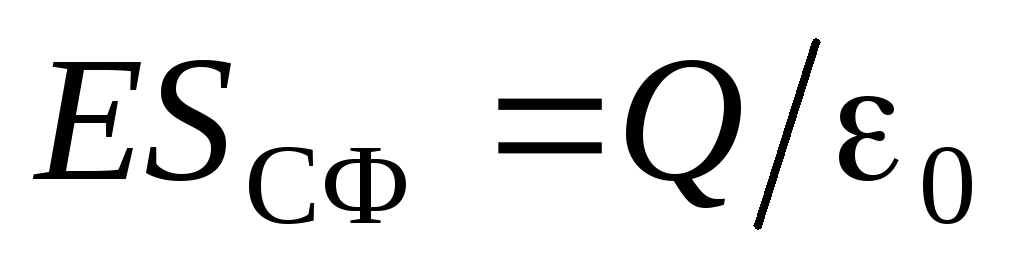
  
  . S obzirom na to
  
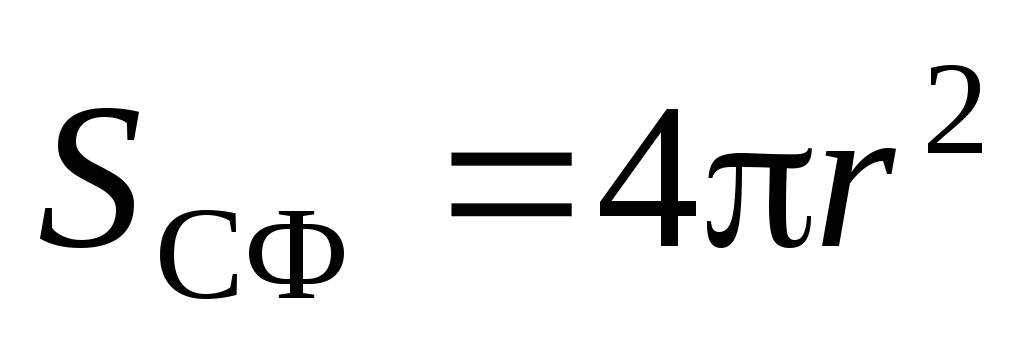  Dobićemo:

  
  .

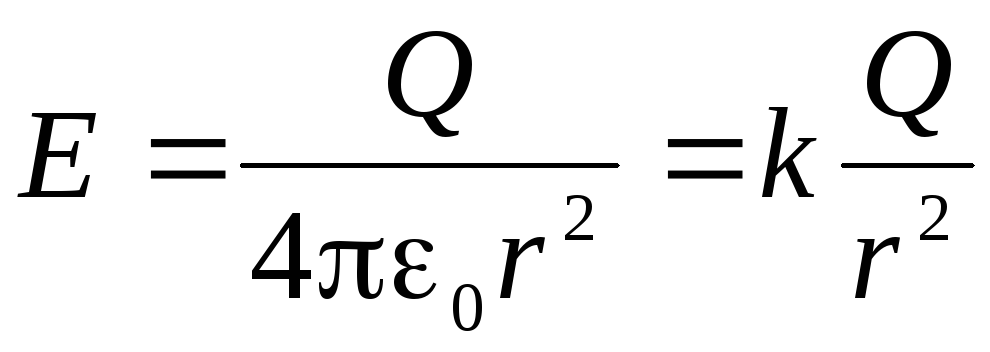  Izračunajte potencijal električnog polja. Povoljnije je za početak sa vanjskim
  
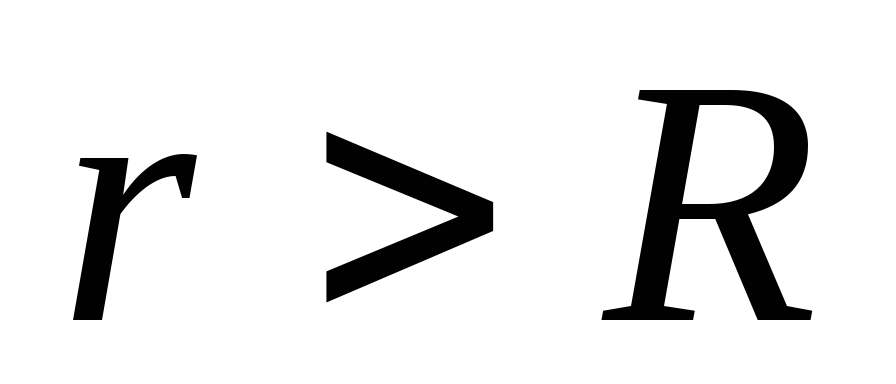  Kao što znamo da se na beskrajnoj udaljenosti od centra sfere, potencijal se uzima jednak nuli. Upotreba jednadžbe (1.11, a) Dobivamo diferencijalnu jednadžbu sa odvajanjem varijabli: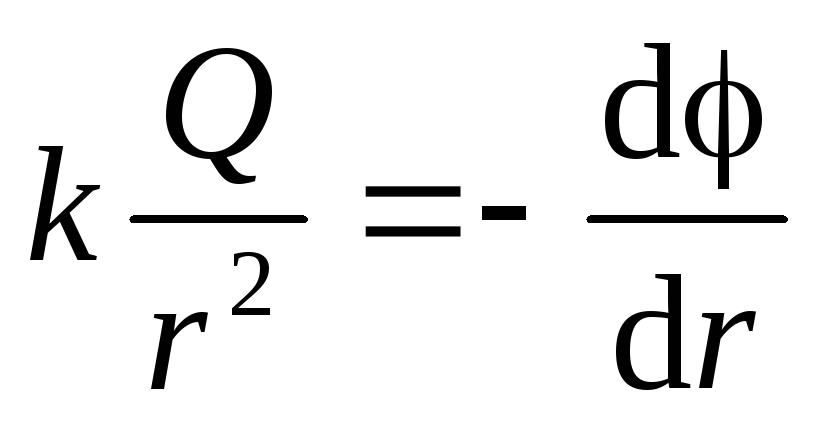

  
  
  
  
  
  
  
  
  
  
  
  
  
  .

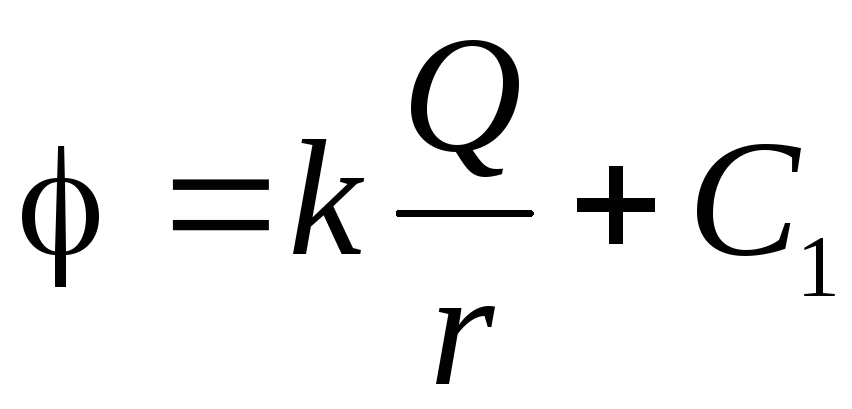  Konstantan
  
  , ukoliko
  
  za
  
  . Dakle, u vanjskom prostoru (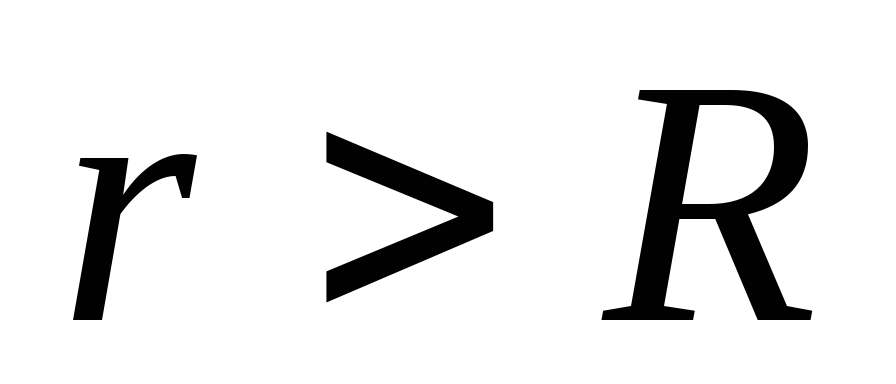
  
  ):
  
  .

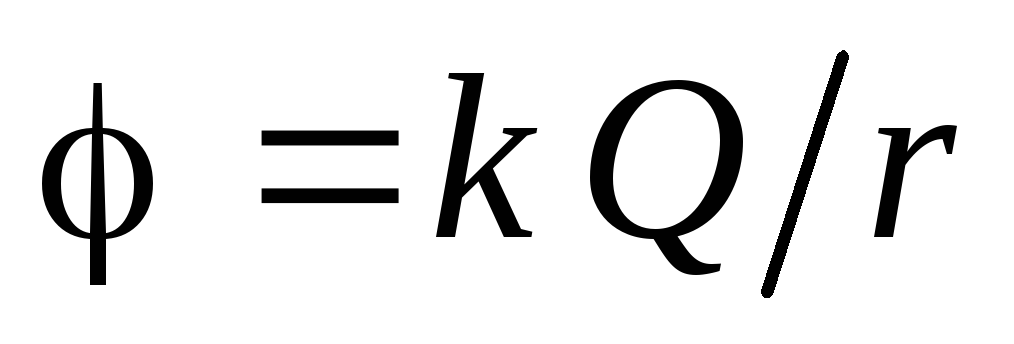  Bodovi na površini napunjene sfere (
  
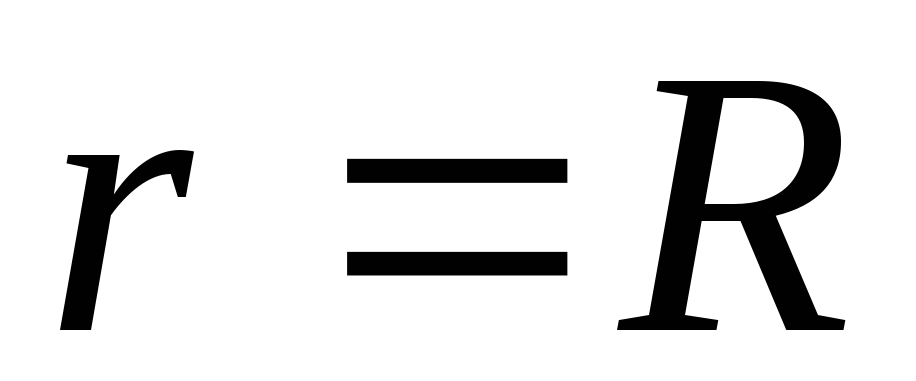  ) imaće potencijal
  
  .

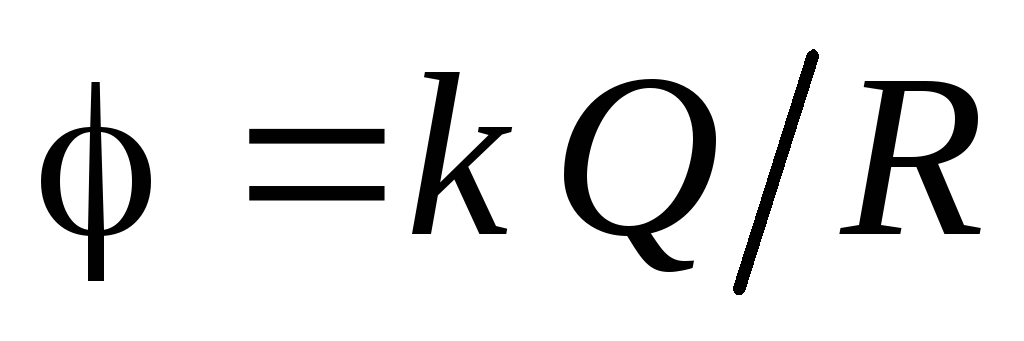  Razmislite o području
  
  . U ovoj regiji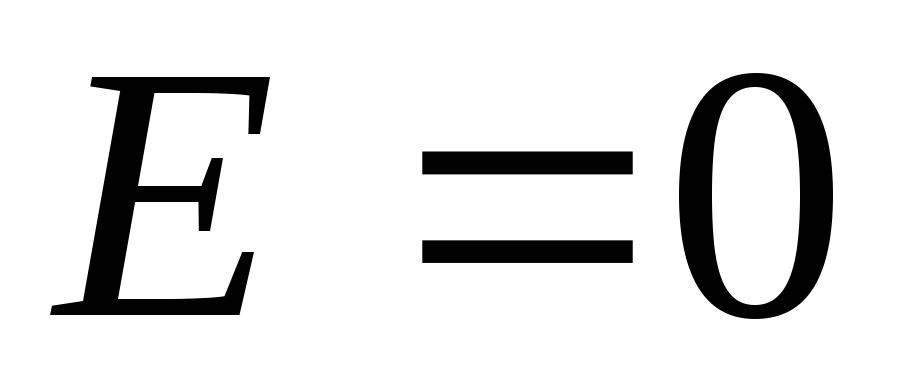
  
  , dakle, iz jednadžbe (1.11, a) dobivamo: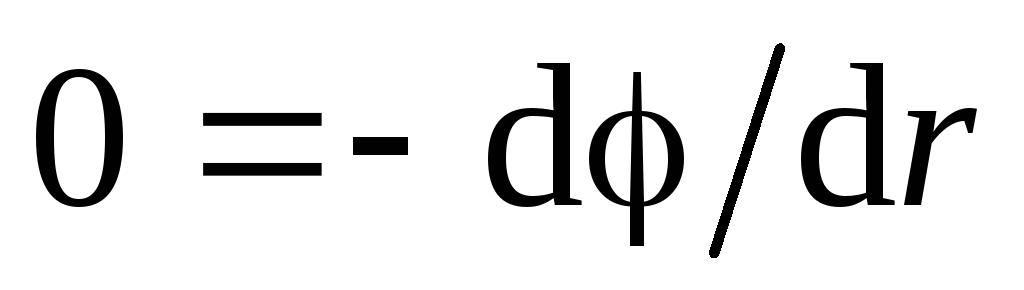
  
  
  
  
  
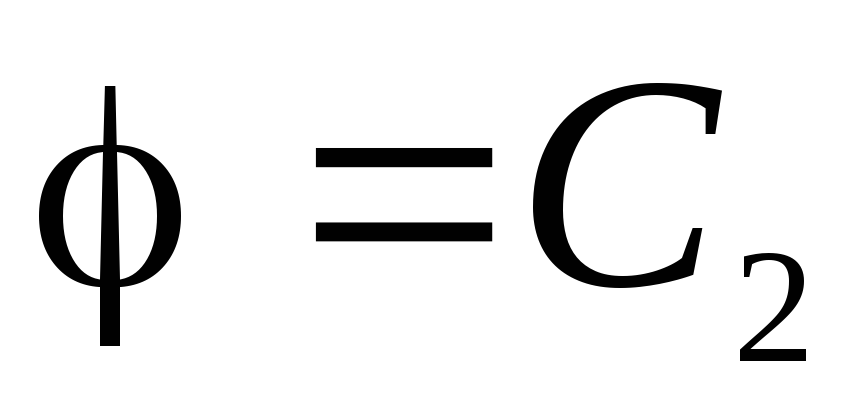  . Zbog kontinuiteta funkcije
  
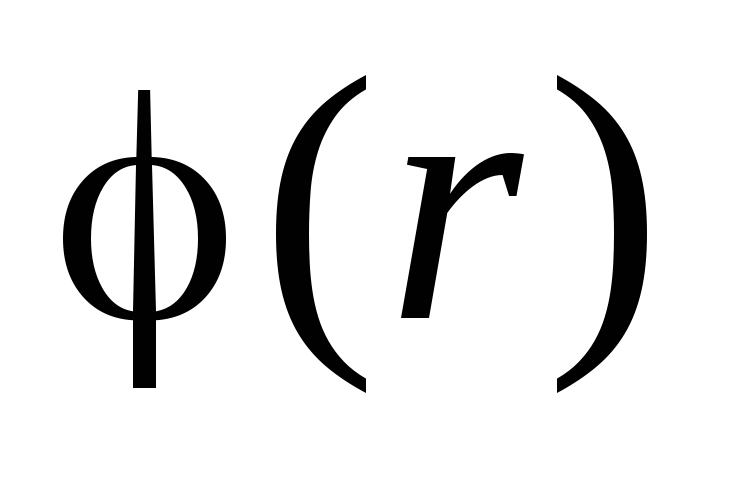  konstantan mora biti jednaka vrijednosti potencijala na površini napunjene sfere: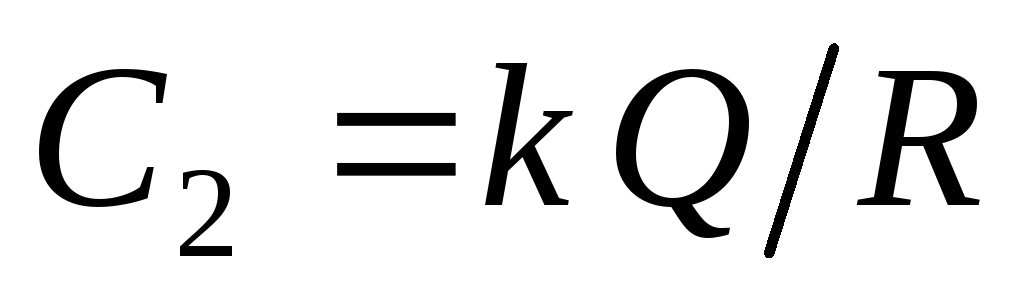
  
  . Dakle, potencijal u svim tačkama u sferi:
  
  .

  

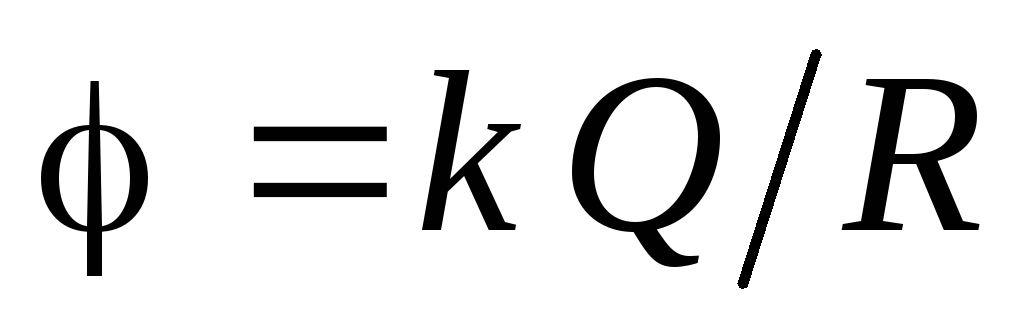  Dakle, dobili smo da tenzije i potencijal električnog polja stvorene ravnomjernim nabijenim sferom, izvan sfere jednake su napetosti i potencijal polja stvorenog polja tačka naplate iste veličine Kao naboj sfera smještenim u sredinu sfere. U unutrašnji prostor Polje je odsutno, a potencijal u svim točkama je isti. Električno polje (dalekovodne snage i ekvipotencijalne površine) napunjene sfere prikazane su na slici. 1.12. Pretpostavlja se da se sfera pozitivno tereti. Izvan sfere dalekovoda i distribuira se u prostoru na isti način kao i dalekovodne linije točke.

  

  Na slici. 1.13 prikazuje grafiku ovisnost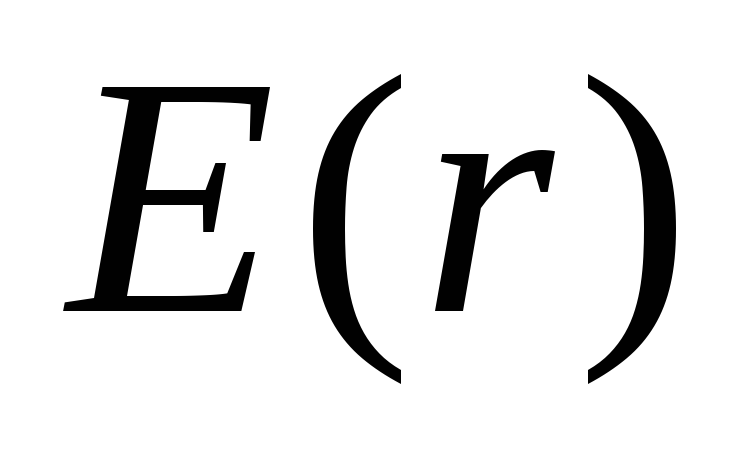i
  
  i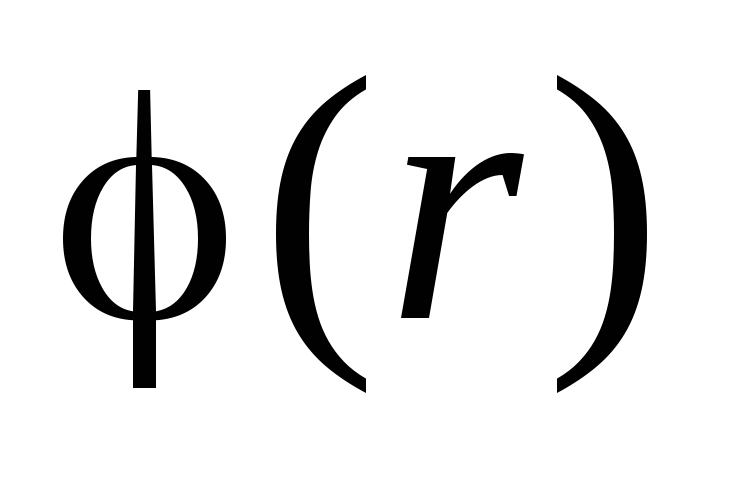
  
  . Funkcija
  
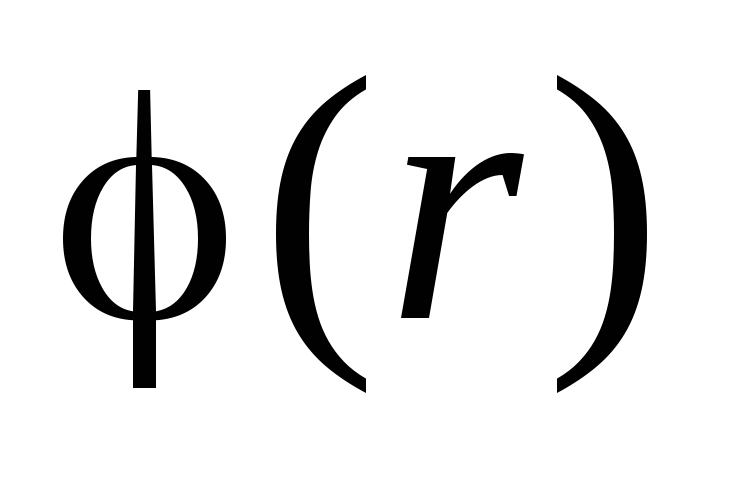  kontinuirana i funkcija
  
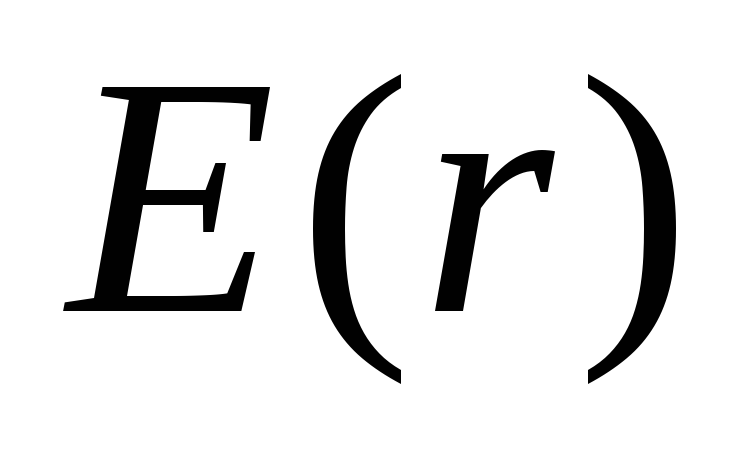  skošano se mijenja prilikom kretanja preko granice napunjene sfere. Veličina skoka je jednaka
  
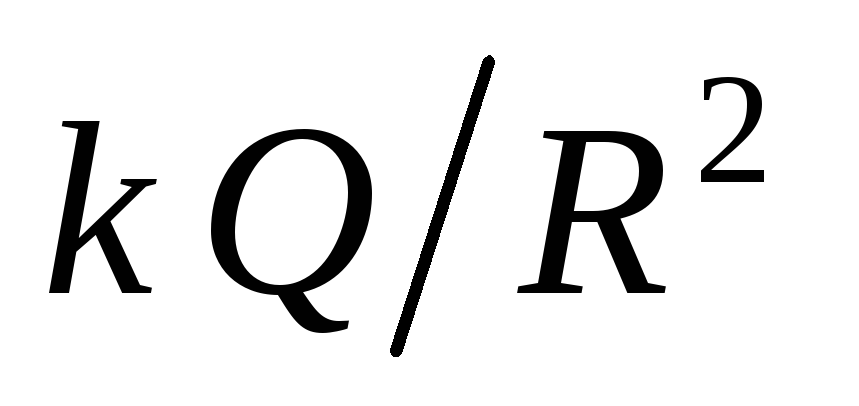  . Zaista, u blizini nabijene sfere (
  
  ) snaga polja u vanjskom prostoru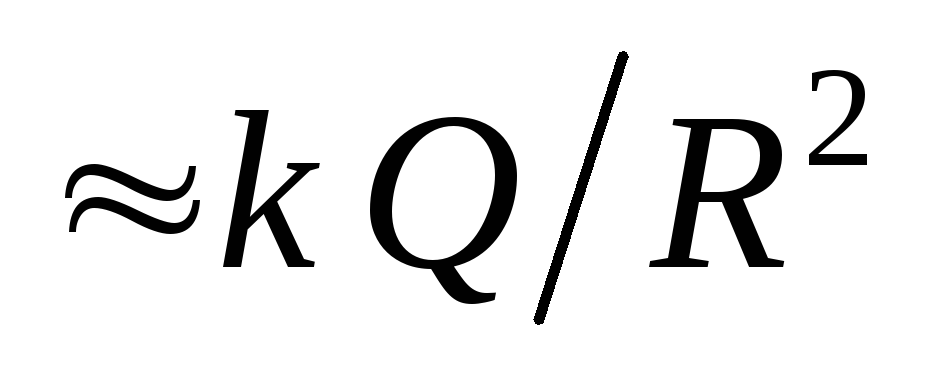
  
  , a unutra je nula.

  Veličina skoka može se izraziti kroz površinski gustoću napunjenosti na sferi:

  
  .

  Imajte na umu da je ovo cjelokupna imovina elektrostatičkog polja: na nabijenoj površini, projekcija napetosti na smjeru normalnog uvijek napušta skok
  
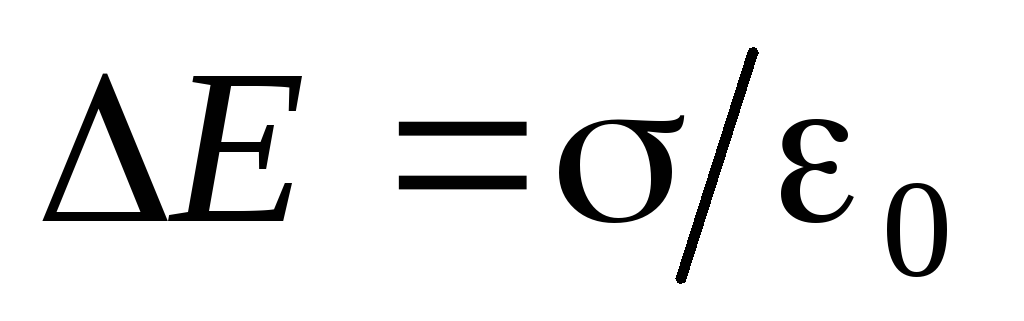  bez obzira na površinski oblik. Preporučujemo provjeru ovog principa za polje jednolično napunjenog ravnine i polja dva paralelna punjena ravnina (primjeri 1.3, 1.4).

  Sa stajališta matematike, kontinuitet potencijala na tačkima nabijenog površine znači to
  
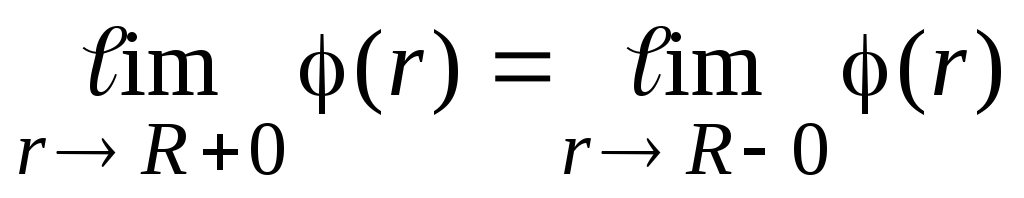  . Sa stanovišta fizike, kontinuitet funkcije
  
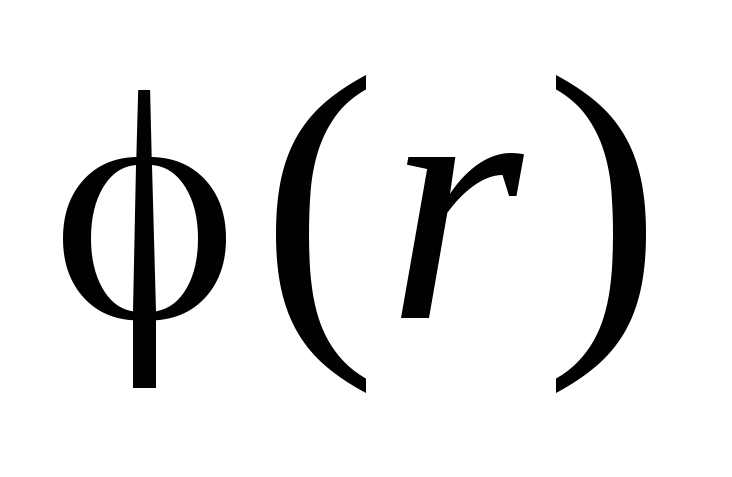  može se objasniti na sljedeći način. Ako bi potencijal na granici nekog regija imao skok (pauzu), a zatim beskonačno malim kretanjem neke optužbe od točke 1 leži na jednoj strani granice, do točke 2, leži na drugoj strani, konačni rad bi se izveo
  
  gde i  Potencijali bodova 1 i 2, odnosno i vrijednost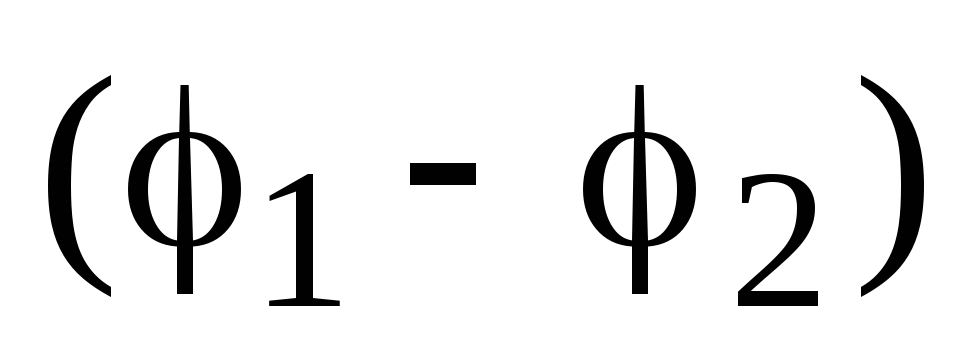
  
  jednaka veličini brze potencijale na granici regije. Krajnji rad, savršen na beskonačno malom potezu, znači da bi na granici particije bila beskonačno velike sile, što je nemoguće.

  Snaga električnog polja, za razliku od potencijala, na granici regije može se razlikovati vrlo oštro (skakanje).

  Primjer 1.6.Dvije koncentrične sfere radijusa i (
  
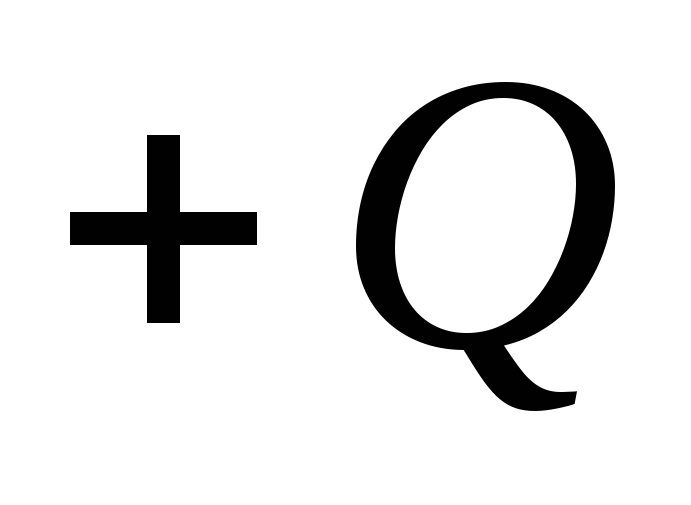  ) Podjednako optuženi za jednake u modulu, ali suprotno znakom optužbi
  
  i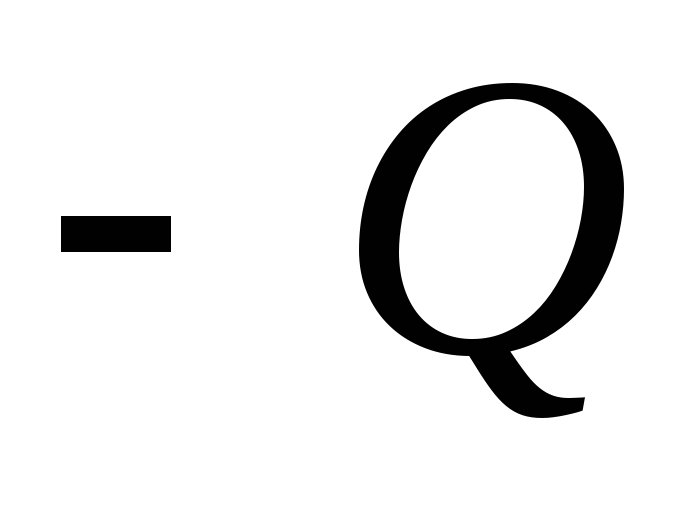
  
  (sferni kondenzator). Odredite napetost i potencijal električnog polja u cijelom prostoru.

  Odluka. Rješenje ovog problema također bi moglo početi upotrebom Gauss Teorem. Međutim, koristeći rezultate prethodnog primjera i principa superpozicije (1,13, 1.14), odgovor se može dobiti brže.

  Na vanjskim točkama prostora (
  
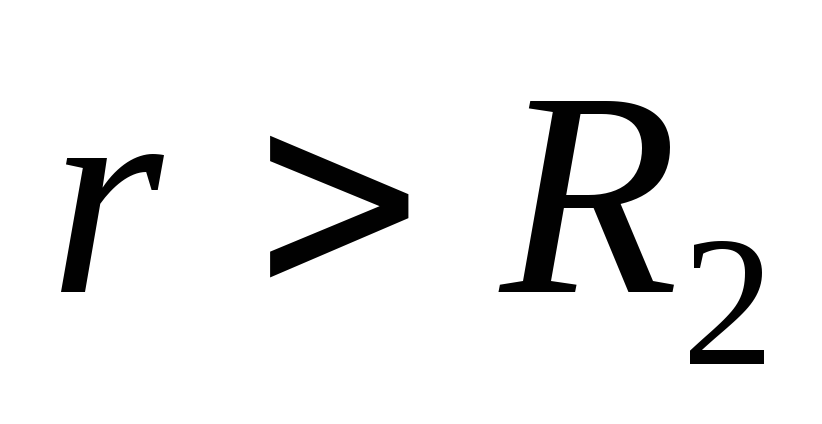  ) Električno polje kreira se naknadama obje sfere. Veličina terenskog intenziteta prve sfere
  
  i usmjeren iz sfera duž radijusa. Veličina intenziteta drugog polja sfere je ista
  
  Ali suprotno je usmjereno. Shodno tome, prema principu superpozicije, u svim vanjskim točkama prostora, električno polje će biti odsutno
  
  .

  Razmotrite tačke prostora između sfera (
  
  ). Ove su točke interne za negativno nabijenu sferu, tako u ovom području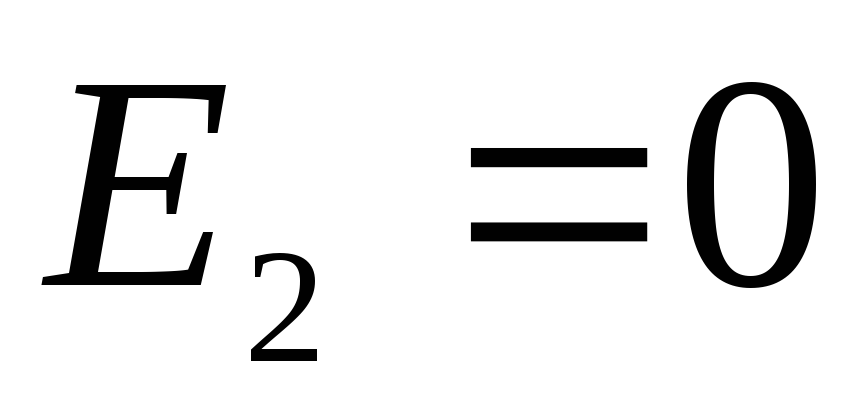
  
  (Vidi primjer 1.5). Za pozitivno nabijenu sferu, ove su točke vanjske, tako
  
  . Dakle, veličina terenske snage u ovom području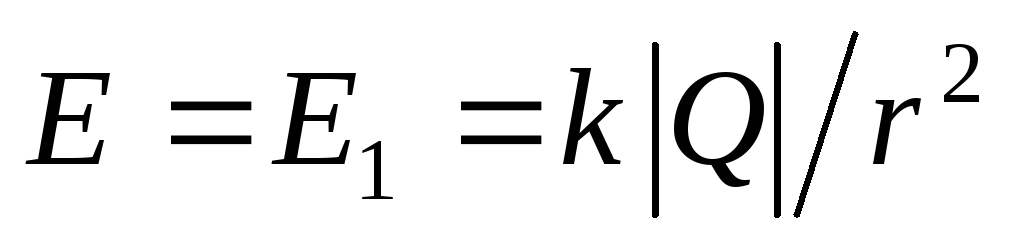
  
  . Ovdje polje stvara samo manje troškove.

  Konačno, u unutrašnjim točkama prostora (
  
  )
  
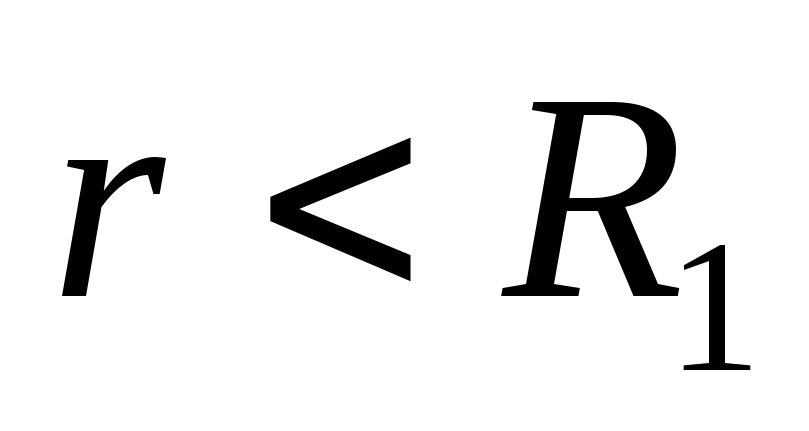  i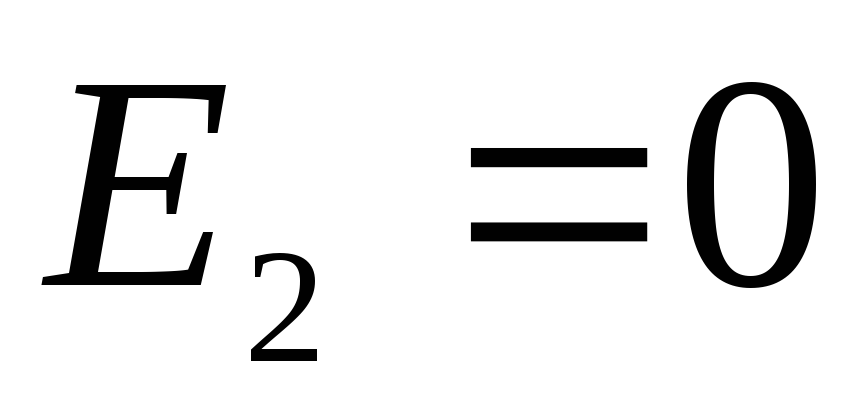
  
  Dakle, ne postoji električno polje na tim tačkama.

  Slično tome, možete primijeniti princip superpozicije i potencijala. Dobivaju se sljedeći rezultati:

  
  :
  
  ;

  
  :
  
  ;

  
  :
  
  .

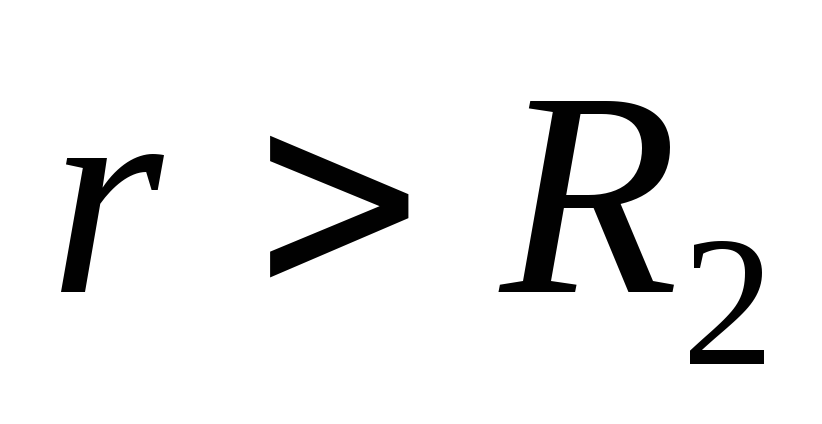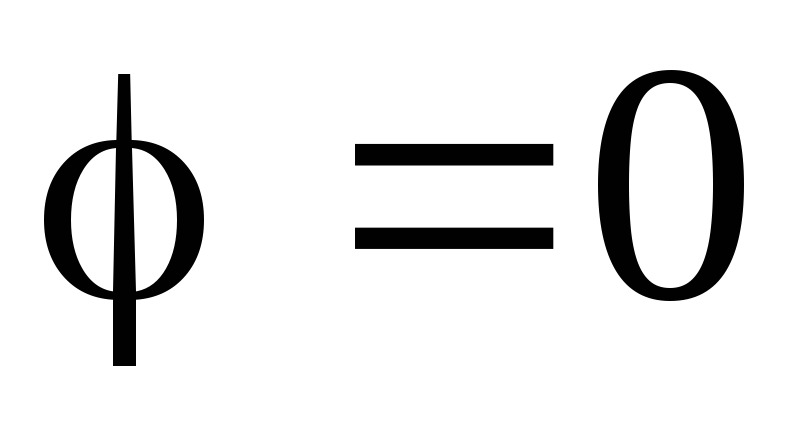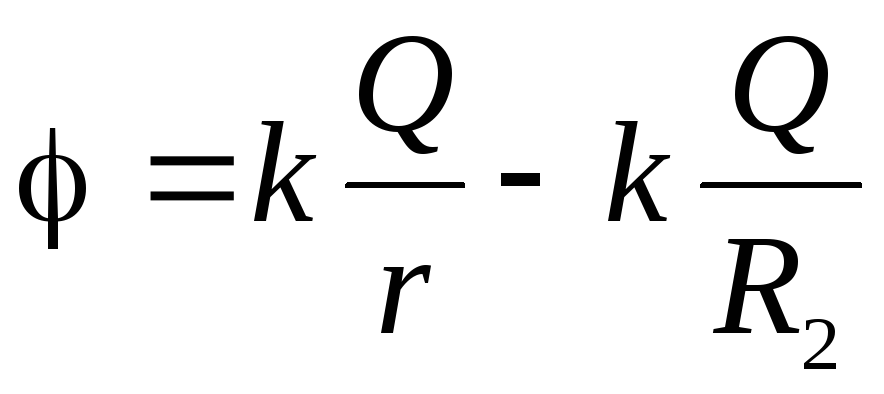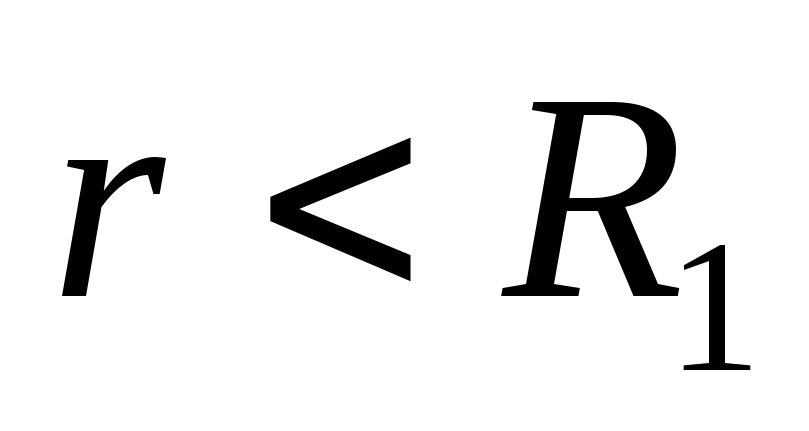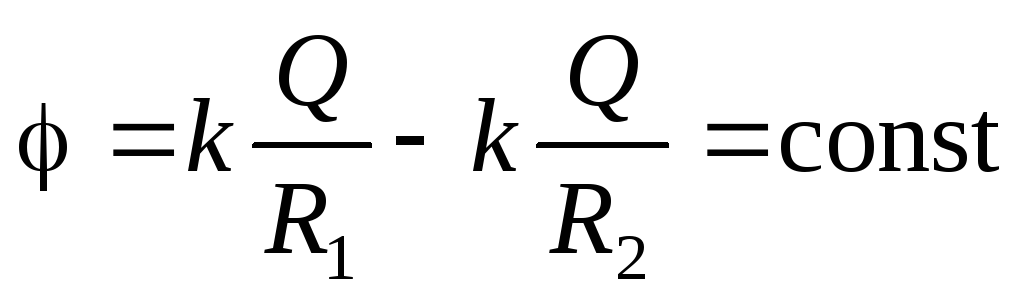  Preporučujemo samostalno dobivanje tih rezultata, kao i shematski prikaz električnog polja i grafikona
  
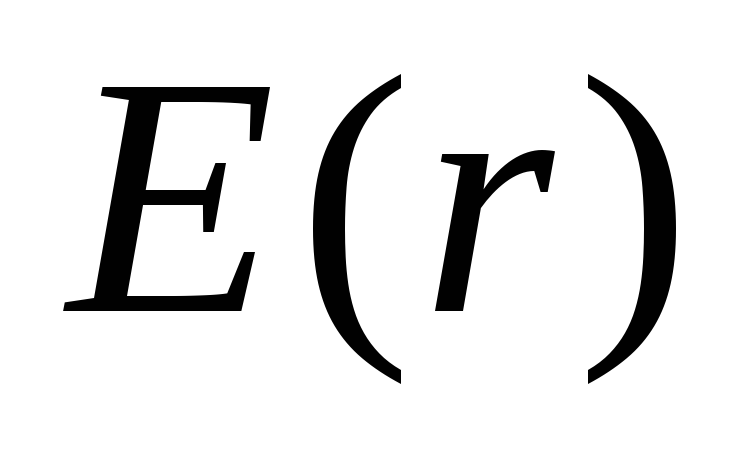  i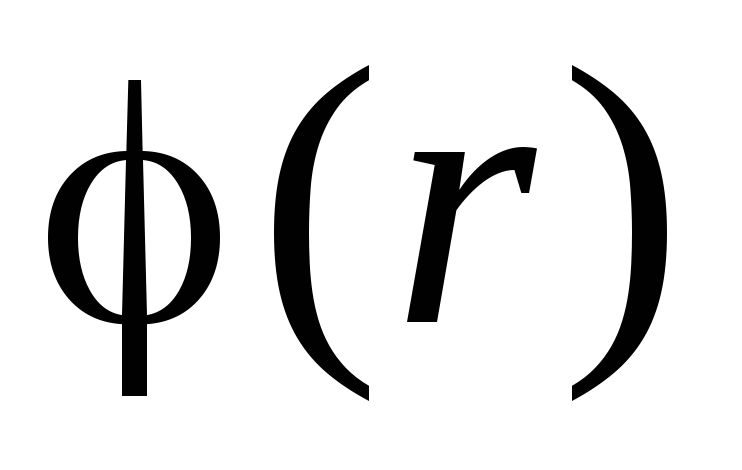
  
  .

  ali b.

  

  Poznavanje napetosti vektora elektrostatičkog polja na svakoj svojoj točki, ovo polje možete predstaviti jasno koristeći snage napetosti (vektorske linije 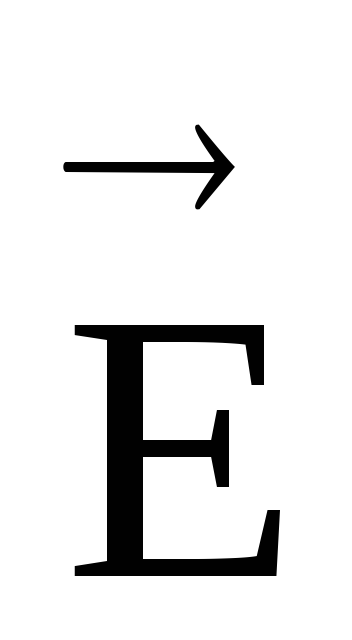). Napetosti napetosti se vrše tako da ih tangenta na svakoj tački poklapa sa smjerom vektora zatezacije (Sl. 1.4, ali).

  Broj liniji koji čine jedinicu DS platformu okomito na njih proporcionalna su vektorskom modulu (Sl. 1.4, b.).

  Linije napajanja pripisuju se smjeru koja se podudaraju s smjerom vektora . Rezultirajući obrazac raspodjele napetosti omogućava prosuđivanje konfiguracije ovog električnog polja u različitim točkama. Počnite dalekovod pozitivne optužbe I završava negativnim optužbama. Na slici. 1.5 prikazuje liniju snage tačke troškova (Sl. 1.5, ali, b.); Sistemi dvaju varijance (Sl. 1.5, u)  Primjer nehomogenog elektrostatičkog polja i dva paralelna varijalno napunjena aviona (Sl. 1.5, g.)  Primjer homogenog električnog polja.

  1.5. Distribucija optužbi

  U nekim slučajevima, pojednostavljivanje matematičkih proračuna, prava raspodjela tačke diskretnih troškova povoljno je zamijenjena izmišljenom kontinuiranom distribucijom. Tokom prelaska u kontinuiranu raspodjelu troškova, koncept gustoće optužnice  linearna , površina  i volumetrijska , i.e.

  
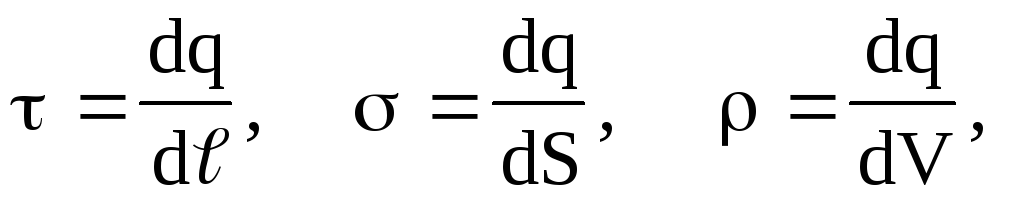  (1.12)

  gdje se DQ  naplaćuje podijeljeno prema elementu dužine
  
  , Površinski elementi i element za volumen DV.

  Uzimajući u obzir ove distribucije formule (1.11) mogu se zabilježiti u drugom obliku. Na primjer, ako se naboj distribuira u količini, a zatim umjesto q moram koristiti DQ \u003d DV, a simbol iz iznosa zamijenjen je integralnom, a zatim

  
  . (1.13)

  1.6. Električni dipol.

  Da bi se objasnio pojave povezane sa optužbama u fizici, koncept se koristi Električni dipol.

  Sistem dva jednaka u veličini višedimenzionalnih troškova, udaljenost između čega je mnogo manja od udaljenosti do proučavanih mjesta prostora, naziva se električnim dipolom. Prema definiciji dipola  + q \u003d q \u003d q.

  

  Direktno povezivanje variepete troškova (stubovi) naziva se dipolska os; Točka 0  Centar dipola (Sl. 1.6). Električna dipola se odlikuje dipol za rame: Vektor usmjeren iz negativnog naboja na pozitivno. Glavna karakteristika dipola je električni dipolni trenutak \u003d TUŽILAC WHITING - PITANJE: . (1.14)

  U apsolutnoj vrijednosti

  p \u003d Q. 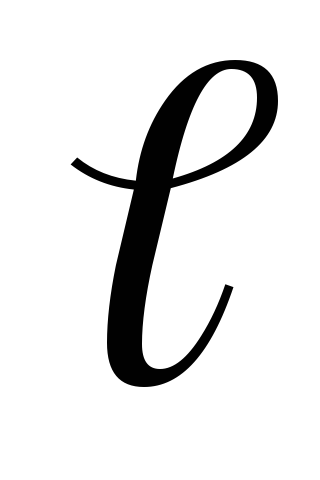. (1.15)

  U x, električni dipolni trenutak mjeri se u raonicima pomnoženo s brojilom (CL m).

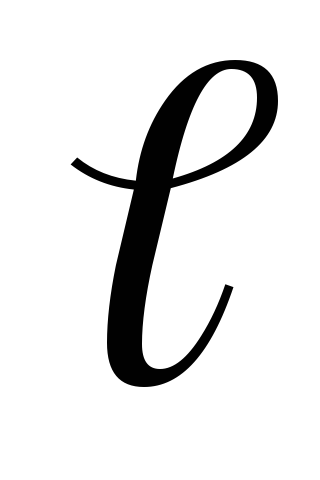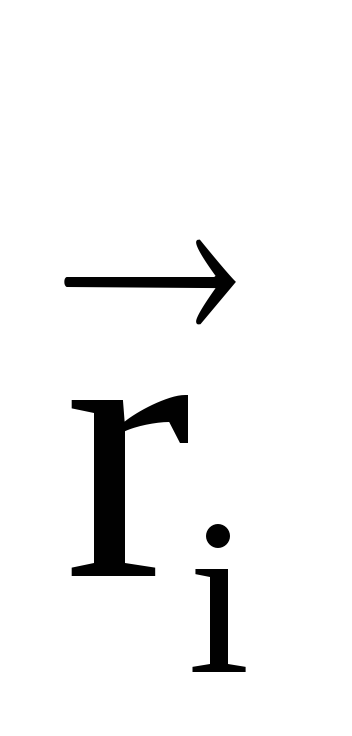
  Izračunajte potencijal i napetost električnog polja dipola, s obzirom na to, ako  r.

  Potencijal električnog polja stvorenog od strane sustava punjenja u proizvoljnoj točki karakteriziran od radijusa , Pišite u obrascu:

  
  

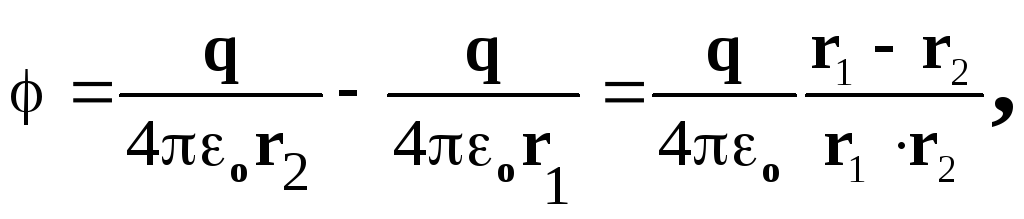
  gdje r 1 r 2  r 2, r 1  r 2  r \u003d
  
  , kao 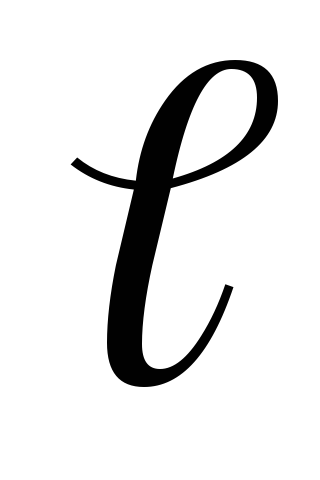 r;   ugao između radijusa-vektora i 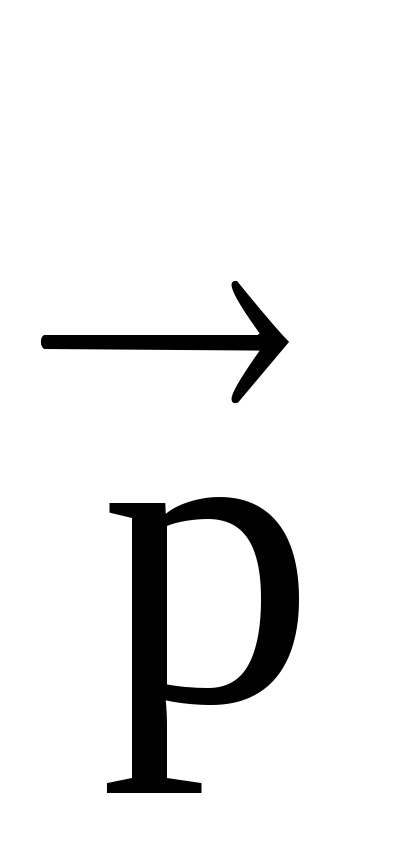(Sl. 1.6) . S tim, imamo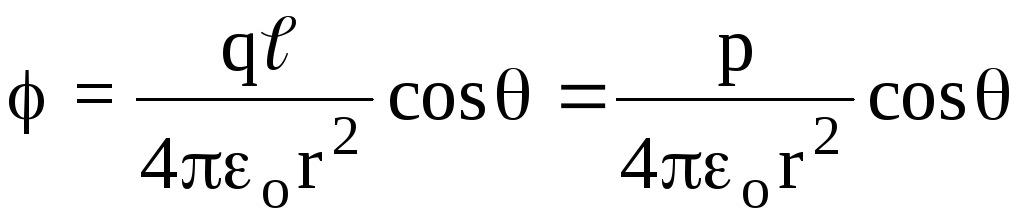

  
  . (1.16)

  Koristeći formulu koja povezuje potencijalni gradijent s napetošću, nalazimo intenzitet stvoren električnim poljem dipola. Spider vektor električni dipolska polja su dvije međusobno okominske komponente, tj.
  
  (Sl. 1. 6).

  Njihov prvi od njih određeni su kretanjem točke koju karakteriše radijus (po fiksnoj vrijednosti ugla), I.E. Vrijednost e  Pronađite diferencijaciju (1,81) od R, I.E.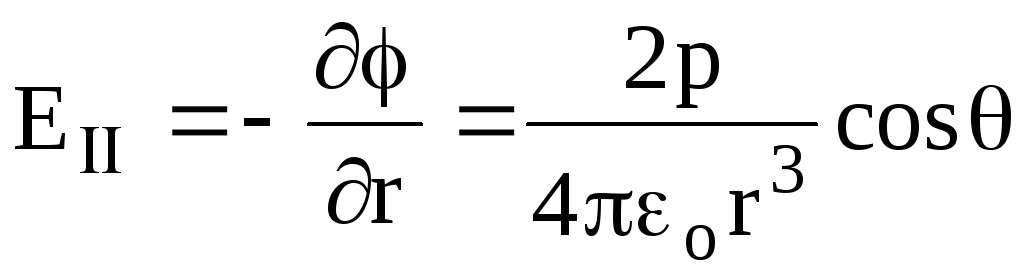

  
  . (1.17)

  Druga komponenta određuje se kretanjem tačke povezane sa promjenom uglova  (sa fiksnim R), I.E. e  Mi smatramo diferencijacijom (1,16) od strane :
  
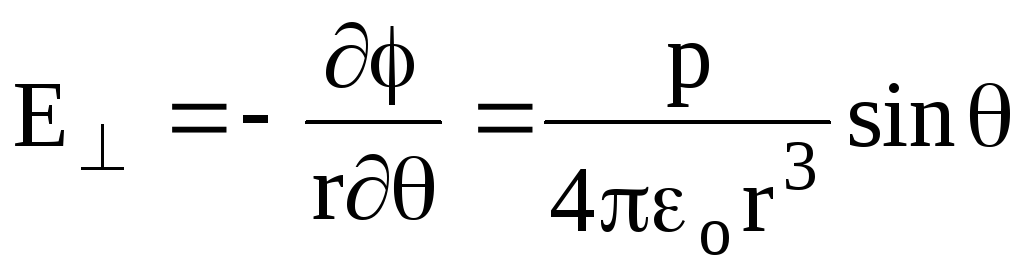  , (1.18)

  gde
  
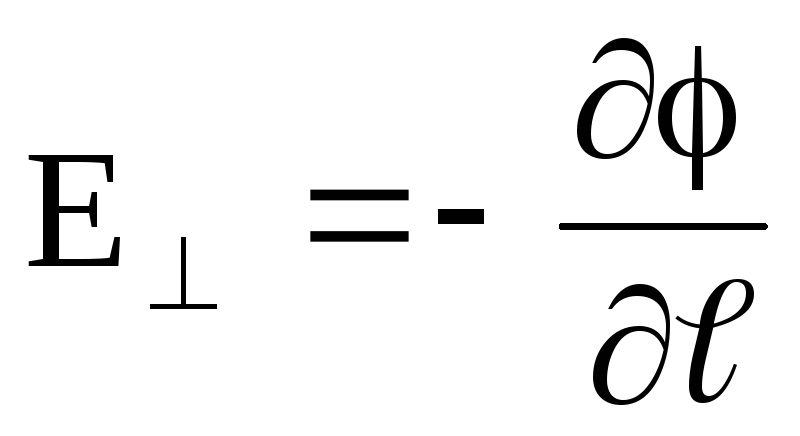  , D. 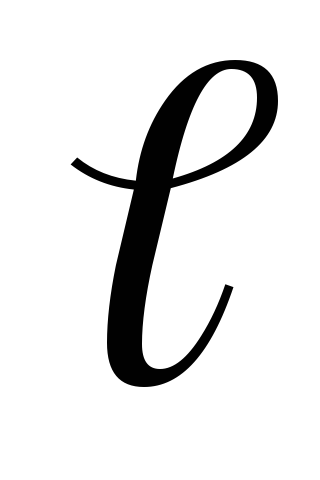\u003d RD.

  Rezultat zatezanje E 2 \u003d E  2 + E 2 ili nakon zamjene
  
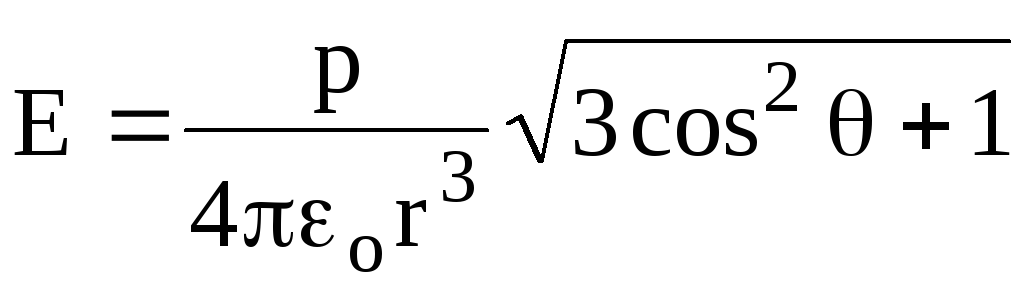  . (1.19)

  Komentar: Na  \u003d 90 o
  
  , (1.20)

  i.e. napetost na mjestu na pravoj liniji koja prolazi kroz sredinu dipola (T. O) i okomito na osovinu dipola.

  Na  \u003d 0
  
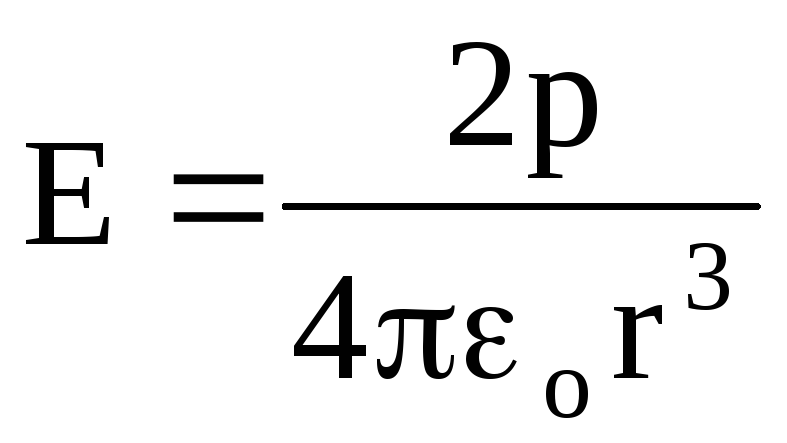  , (1.21)

  i.e. na mjestu nastavka izravnog koji se podudaraju sa osi dipola.

  Analiza formula (1,19), (1.20), (1.21), (1.21) pokazuje da se snaga električnog polja dipola smanjuje sa daljinom obrnuto proporcionalnom R3, tj. Brže nego za točku (obrnuto proporcionalno R 2).