1. piemērs.Noteikt bezgalīgas plaknes lauka spēku un potenciālu, vienmērīgi apsūdzot virsmas blīvums Maksa s. Dielektriskā konstante apkārtne e.

No simetrijas uzdevuma ir skaidrs, ka spriedzes līnijas elektriskais lauks Jābūt paralēli taisni, perpendikulāri uzlādētajai virsmai, kā parādīts RI C.1.2. Līdz ar to uzlādes plaknes lauks ir viendabīga.

Izvēlieties aizvērtu virsmu tiešā cilindra garuma veidā. l. Ar fonda platību S., kā tas parādīts attēlā. Sakarā ar viendabīgumu lauka spriedzes uz apakšējo un augšējo bāzi cilindra tāda pati izmēra un sakrīt virzienā ar pozitīviem standartiem uz šīm virsmām. Turklāt mēs ņemam vērā, ka spriedzes vektora plūsma ir klāt. tāpēc

Pilnīga maksa ierobežotas cilindriskās virsmas tilpumā ir vienāda ar q \u003d Ss.. Tad un.

Plaknes lauka potenciāls.

Iegūtajā izteiksmē No - pastāvīga integrācija, un ass Oh Perpendikulāri plaknei. Ņemot potenciālu uz virsmas plaknes vienāds ar nulli, mēs saņemam C \u003d.0.

Visbeidzot.

2. piemērs.Noteikt spēku un potenciālu elektrisko lauku bezgalīgu pavedienu, vienmērīgi apsūdzēts ar lineāru blīvumu maksas t. Vides dielektriskā caurlaidība E.

No aksiālā simetrijas problēmas, no tā izriet, ka pavediena lauka līniju pavedieni ir radiālo staru sistēma, kas rodas no simetrijas ass, kas pieder pie simetrijas ass. Tad pie punktiem vienādojies no pavediena, lauka stiprums ir tāds pats. Izvēlieties taisnu cilindra garumu kā slēgtu virsmu l.ar fonda rādiusu r.Kura ass sakrīt ar pavedienu (sk Fig.1.3). Šādā gadījumā spriedzes vektora plūsma, izmantojot cilindra pamatni, un pilnā plūsma caur slēgto virsmu ir vienāda ar plūsmu caur cilindra sānu virsmu s.:

Jo Katrā cilindra sānu virsmas punktā virziens sakrīt ar normālu virzienu šajā brīdī, un E (r) \u003d constT.

Pilna uzlādes ieslodzītais cilindra tilpumā q \u003d tl. Tad saņemiet

Vītnes lauka potenciāls

gleie ir pastāvīgs No nosaka nulles potenciāla punkta izvēle

3. piemērs. RADIUS RF ar sfērisku dobumu rādiusā A Centrā ir jāmaksā ar lādiņa blīvuma mainīgo ar lineāro likumu R \u003d A (R - A), kur ir konstanta vērtība, un R ir attālums no centra bumba. Noteikt bumbas elektriskās jomas spriedzi un potenciālu. Dielektriskā konstante Bļoda un vide, lai ņemtu vienādu ar 1.

No sfēriskā simetrijas uzdevuma izriet, ka elektriskā lauka stiprums ir atkarīgs tikai no attāluma r. no bumbas centra, t.i. E \u003d E (R)Un vektora līnijas ir radiālie stari, kas rodas no koordinātu sākuma, apvienojot ar bumbu centru. Tajā pašā laikā uz jebkuras sfēriskas virsmas r \u003d const. Lauka stiprums ir vienāds vienā vienā šīs virsmas vietā, un virziens sakrīt ar normālas virsmas virzienu. Tāpēc, lietojot Gauss teorēmu kā slēgtu virsmu, ir ērti izvēlēties virsmu r \u003d const..

Apsveriet elektriskā lauka stiprības vektora plūsmu caur sfērisku virsmu. r.< a . Jo Dobumā nav maksas, elektriskā lauka stiprības vektora plūsma caur sfērisku virsmu r.< a vienāds ar 0, tāpēc elektriskais lauks Nav dobuma.

Ļaujiet virsmas rādiusam, caur kuru tiek aprēķināta sprieguma vektora straume, atbilst nevienlīdzībai a.< r < R . Tad spriedzes vektora plūsma

No otras puses, šī plūsma ir precīza e 0 vienāds ar lādiņu, kas noslēgta sfēriskā slāņa tilpumā, kuru ierobežo radiolu sfēras bet un r.:

Pa šo ceļu,

Un a.< r < R .

Apsveriet elektriskā lauka stiprības vektora plūsmu caur sfēras virsmu r\u003e R.. Šeit joprojām ir N. \u003d, un maksa, kas iekļauta aplūkojamā apjomā, ir vienāda ar bumbu kopējo maksu, t.i.

Tāpēc, kad r\u003e R..

Aprēķināt bumbas potenciālu. Jo un r.< a Е \u003d 0, tad j 1 \u003d C1,

turklāt Ar 1. - nemainīga. Apgabalā a.< r < R

Jautājums no OROKSA

Divas elektriskās lauka stiprības līnijas nevar krustoties vienā punktā. Vai ir iespējams apgalvot, ka vienā brīdī var šķērsot divas ekvipotiskas virsmas?

Atbilde:Divas ekvivalential virsmas var krustoties vienā punktā, ar nosacījumu, ka lauka stiprums šajā brīdī ir nulle. Faktiski spriedzes vektors nosaka normāla virzienu uz katru ekvivalentu virsmu. Tā kā virsmas krustojas krustojumā, to normāls nesakrīt, un tāpēc elektriskajam laukam nav noteiktu virzienu. Tas ir iespējams tikai ar nulles vērtības lauka vērtību.

Datoru modelis demonstrē attēlu silest līnijas un equipotential virsmas Punktu maksa un sistēmas ar diviem punktiem. Jūs varat mainīt maksu un to zīmju vērtības, kā arī attālumu starp maksām. Uzstādot kursoru jebkurā brīdī, un nospiediet kreiso peles pogu, dators izceļ displeju moduļa elektriskā lauka stiprības vektora un potenciālo φ šajā brīdī. Jāatzīmē, ka sfēriskas ekvivalenciālās virsmas ir iespējamas divu punktu nodevu elektriskajā laukā.

2.7. Potenciālo aprēķinu piemēri

Apsveriet dažu iekasēto struktūru radītā lauka potenciāla aprēķinu.

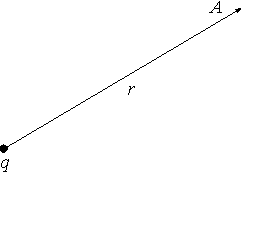
3. attēls. Novērošanas vietas atrašanās vieta saistībā ar point avotu Q lauka

1 .Piemērs Punkts. Izmantojot attiecības (1) un (4) un apvienojot 1. punktu ar novērošanas punktu Bet (3. att.), Un 2. punkts, noņemot bezgalību, mēs saņemam

Komentēt. Vector lauka jēdziens joprojām tika izmantots - vektoru lauki (katrs vietas punkts tiek ievietots saskaņā ar vektoru). Par potenciāla kā funkcija kosmosa punkta ļauj ievadīt jēdzienu skalāra laukā - lauki cipariem (katrs vietas punkts tiek likts atbilstoši precizitāti patvaļīgu piedevu konstante, numurs). Tāpēc nākotnē papildus jēdzieniem elektrostatiskais lauks un lauks izmantos jēdzienu laukā.

2. Piemērs. Mēs uzskatām, ka bezgalīgas viendabīgi jāmaksā lineāra kvēldiega blīvums.

Mūsu uzdevums ir atrast kā funkciju.

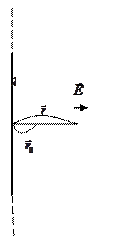
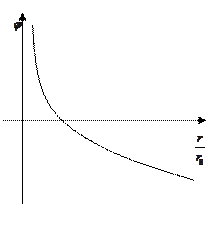Kā jau parādīts bezgalīgi garām pavedieniem:.

Izvēlieties kaut kur punktu, no kura mēs sākam, piemēram, tad, tad

.

Mēs piekrītam, ka sākuma punktā potenciāls ir nulle:, tad

.

Tas ir ar šādu normalizāciju. Ja šādā uzdevumā ir normalizēt, tad mēs saņemam, tas ir, visi potenciāli visos punktos ir bezgalīgi liels. Kam nepieciešama šāda normalizācija? Ja jūs interesē kāds konkrēts telpiskais klāsts, tad ir nepieciešams normalizēt kaut kur netālu no šīs jomas, tad visi potenciāli būs ierobežoti patīkami numuri. No bezgalīgas pavediena nav iespējams izvairīties no bezgalības, par to pašu iemeslu dēļ jums nevajadzētu gaidīt labu rezultātu, jo pavediena punktu fragmentu potenciālu, no kuriem katrs ir normalizēts ar stāvokli.

3. Piemērs. Spot dipola lauka potenciāls (pirmā metode).

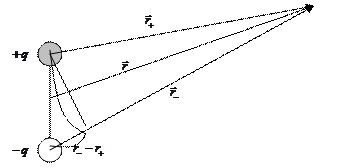Tātad, mēs uzskatām, ka punktu dipols un novērošanas punkts ir pietiekami tālu no šī mūsu hantele.

Paskatīsimies uz šī novērošanas punkta potenciālu.

Pirmkārt, superpozīcijas princips.

Otrkārt, kā jūs zināt

Ņemot vērā, ka ir projekcija par vektoru un to, ka attālums līdz dipola ir ļoti liels, tad tad

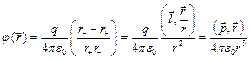
Potenciālā punkta dipola (otrā metode).

Mēs izmantojam gatavo formulu lauka stiprumam:

. Šeit ir tik izteiksme, mēs vienlaicīgi ieveda. Es esmu bijis uz tā.

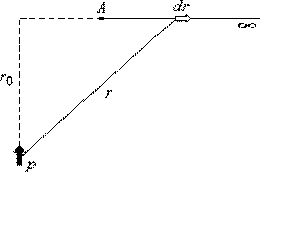
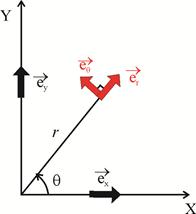Izvēlies šādu virzienu, lai mēs būtu ērti aprēķināt šo integrēto, jo lauks ir potenciāls, rezultāts nebūs atkarīgs no trajektorijas veida. Dipola orientācija, kustības virziens un vektors ir parādīts attēlā. Ņemot vērā dažas attiecības (5).

Apsveriet lauka, kas izveidots ar maksu, vienmērīgi sadalīts bezgalīgā pavediena. Mēs nolēmām šo uzdevumu pēdējā lekcijā, izmantojot elektrisko lauku superpozīcijas principu (sk. 1.11.).

Tagad mēs parādīsim, ka tas ir nedaudz vieglāk aprēķināt šo lauku, izmantojot Gauss teorēmu.

Noteikt lauka stiprumu attālumā r.no pavediena uzlādēts ar pastāvīgu lineāru blīvumu:

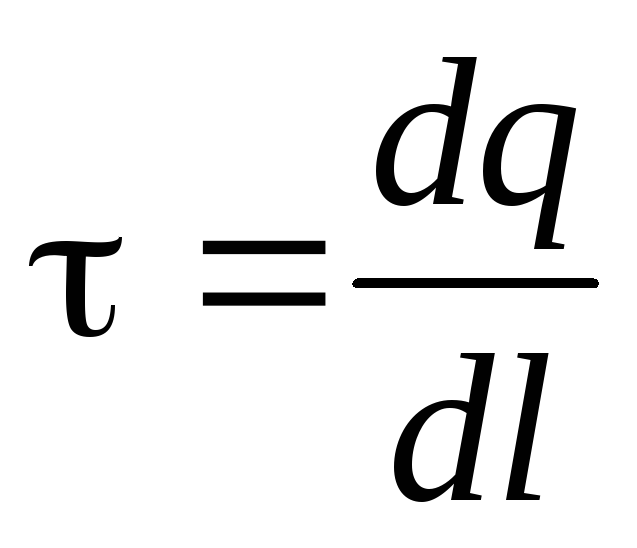, [CL / m] (2.10)

Ap vītni ar slēgtu cilindrisku virsmu (2.7 att.). Cilindra augstums - h.un tās dibināšanas rādiuss - r..

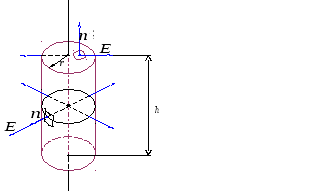
Fig. 2.7.

Lauks, ko rada uzlādētajam pavedienam, ir cilindrisks simetrija. Šajā sakarā sprieguma vektori visos balona sānu virsmas punktos būs vienāda ar moduli un ir vērsti radiāli, tas ir, perpendikulāri cilindra sānu virsmai. Cilindra vektoru bāzēs vada radiāli, "slaidu" uz pamata, veidojot taisnu leņķi ar normālu .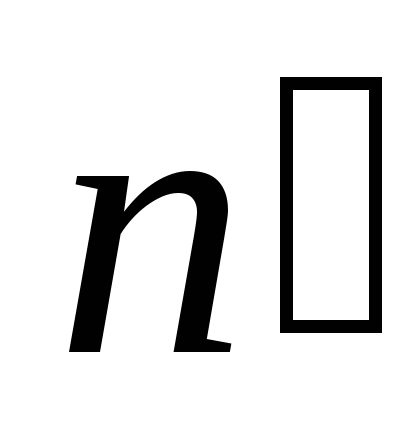

Aprēķiniet plūsmas vektoru caur izvēlētā cilindra virsmu. Pilna plūsma caur šo slēgto "Gaussian" virsmu ir izgatavota no plūsmas caur cilindra sānu virsmu un caur diviem pamatiem:

Pēdējie divi integrāli ir nulle, jo "bīdāmās" uz cilindra vektoru bāzēm nepārtrauciet tos un neradiet nevienu straumi. Formāli šie divi integrāli ir nulle, jo starp vektoriem un 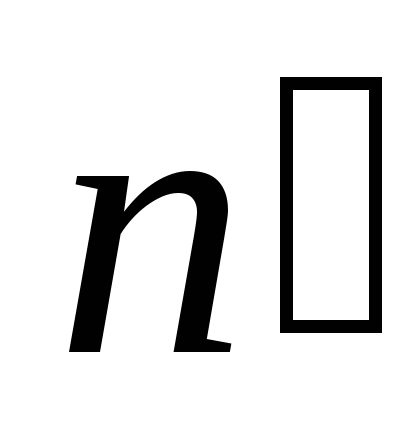taisni leņķis I.

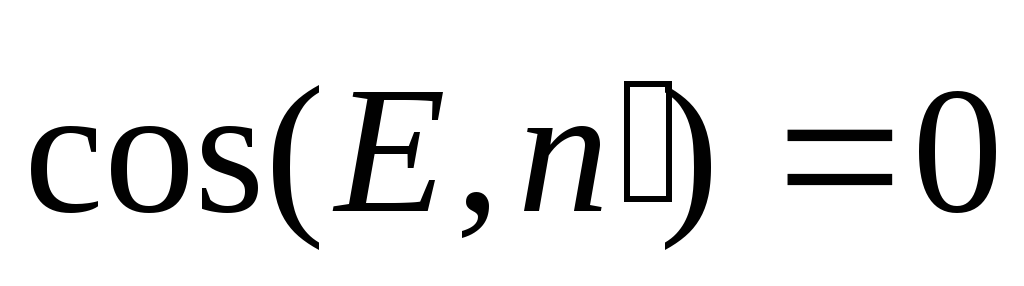. Pa šo ceļu

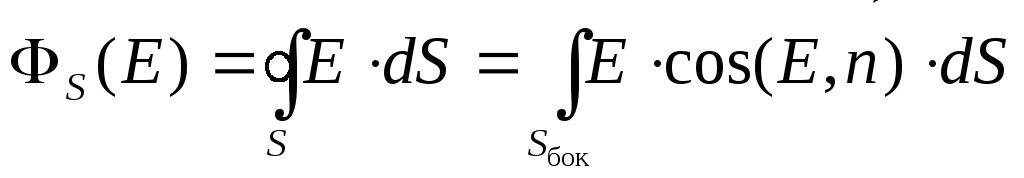
Visos cilindra sānu virsmas punktos E.=E. r. \u003d mīnusi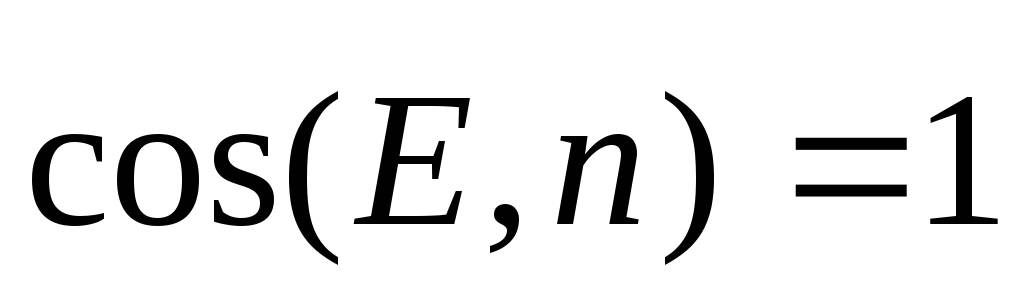

.

Tāpēc plūsma caur sānu virsmu cilindra ir vienāda

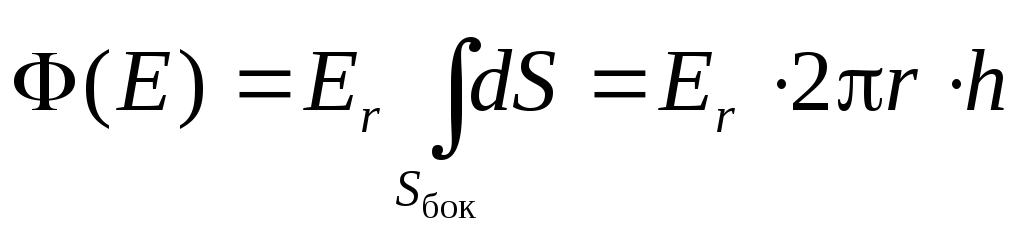(2.11)

Tas ir plūsma elektriskā lauka stiprības vektora, ko aprēķina pēc plūsmas definīcijas.

Tagad mēs izmantojam Gauss Theorem, atzīmējot iepriekšējo lietu, ka "Charge ieslodzītais Gausa virsmas iekšpusē" šajā gadījumā ir koncentrēta uz pavediena stiepjas h.- uz cilindra ass:

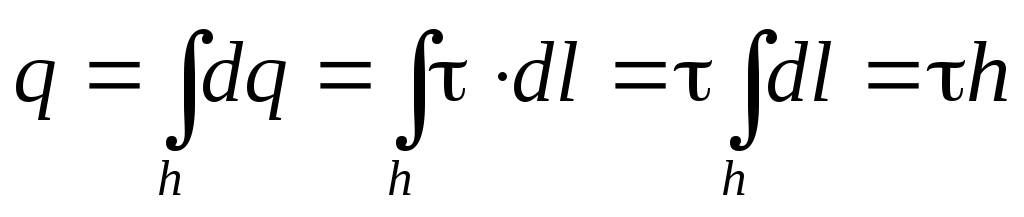
Pa šo ceļu

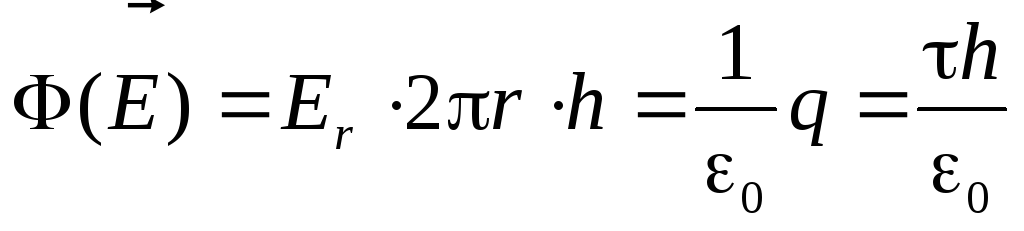(2.12)

No šejienes tagad ir viegli iepazīties ar mums hiperbolisku atkarību no intensitātes lauka no attāluma līdz pavedienam - r.(Sk 1.11).

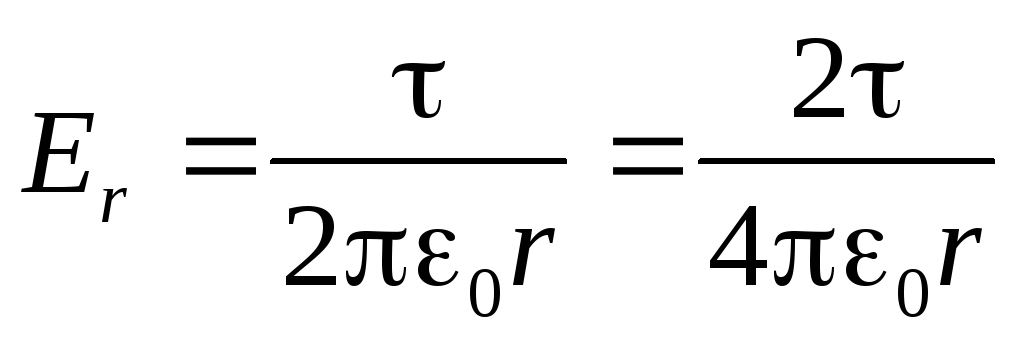(2.13)

1. Infinīta vienmērīgi uzlādēta plakne. Flat kondensatora lauks

Ļaujiet elektriskajam laukam izveidot maksu, vienmērīgi sadalīti pa bezgalīgas plaknes virsmu, ar virsmas blīvumu  (2.8. Att.)

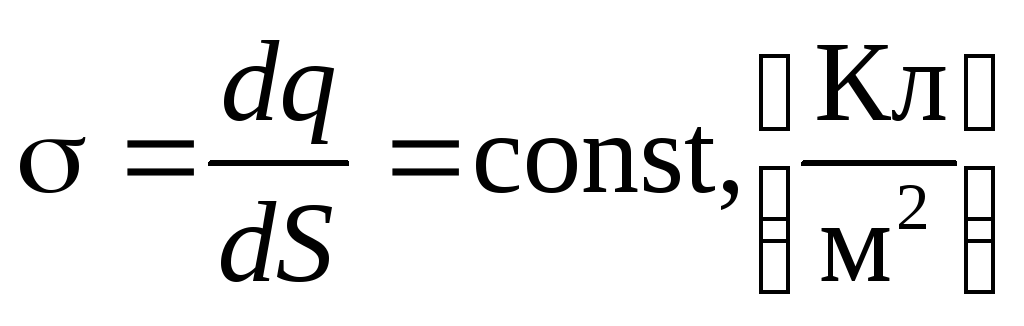
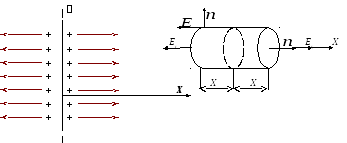
Fig. 2.8.

No uzdevuma simetrijas izriet, ka lauks tiek nosūtīts visur perpendikulāri virsmai. Mēs uzzinām, kā lauka stiprums mainās, jo tas noņem no uzlādētās lidmašīnas.

Kā Gausa virsma ir ērti izvēlēties cilindru. Cilindra ass nosūtīs perpendikulāra lidmašīnu, tā pamatne atrodas attālumā H.simetriski abās virsmas pusēs.

Aprēķiniet sprieguma vektora stiprumu caur cilindra sānu virsmu un pamatni. Šādi no att. 2.8., Stroy vektora plūsma caur cilindra sānu virsmu ir nulle, jo šeit spriedzes vektori "slide" uz virsmas un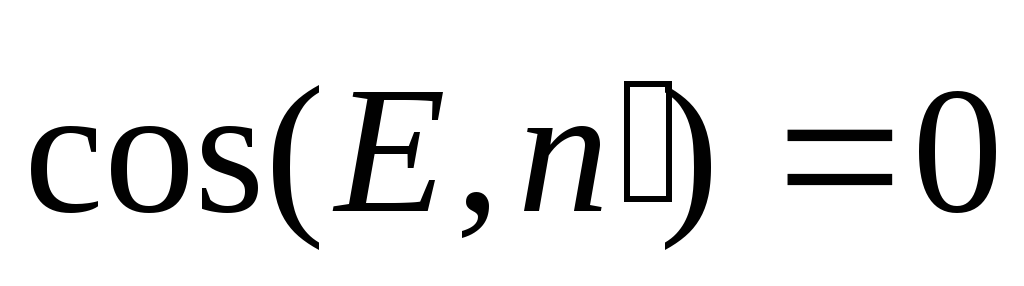

.

Tad pilnu plūsmu caur slēgtu cilindrisku virsmu var rakstīt kā plūsmu caur diviem cilindra bāzēm.

Tā ir vērtība, kas aprēķināta, lai noteiktu plūsmu.

Tagad mēs izmantojam Gauss Theorem, atzīmējot, ka maksa q., "Atrodas iekšpusē Gausa virsmas", šajā gadījumā koncentrējas uz vietni S.=S. OSN, "samazināt" cilindru bezgalīgas plaknes

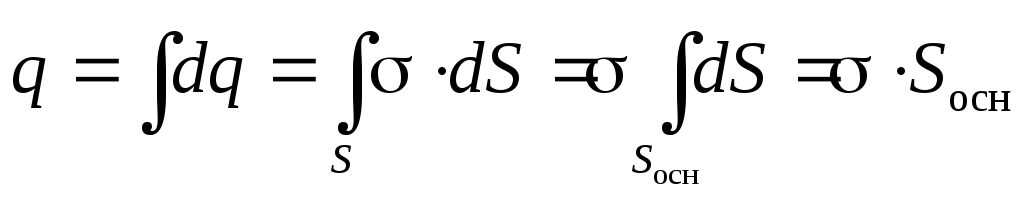(2.15)

Mēs apvienojam rezultātus (2.15) un (2.14) Gausa vienādojumam:

Kur seko

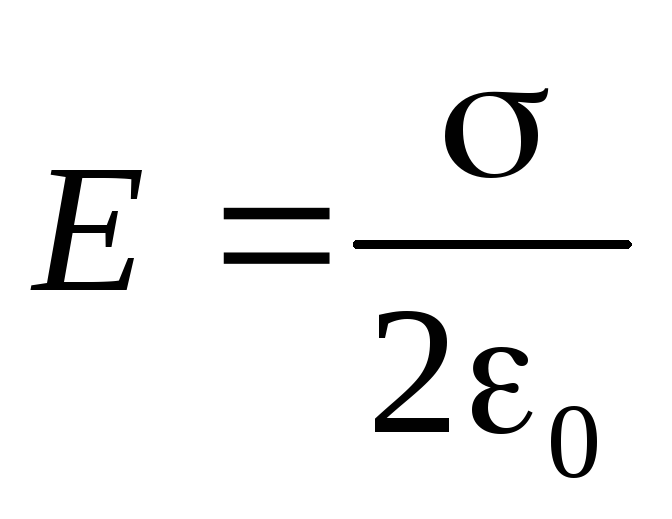(2.16)

Produkcija. Lauks, ko rada bezgalīga vienmērīgi uzlādēta plakne, vienmērīgi. Tas nemainās ar attālumu no uzlādētās virsmas, ne virzienā.

Tagad apsveriet vēl vienu svarīgu piemēru. Ļaujiet laukam izveidot divus bezgalīgas lidmašīnas, variened, bet ar tādu pašu virs lieluma virsmas blīvumu maksas (2.9 att.). Tā ir svarīga elektrostatikas idealizācija - dzīvoklis kondensators. Katrs šī kondensatora atpūtas laiks rada viendabīgu lauku, kuras spriedze, no kuras mēs tikko instalējām (2.16):

.

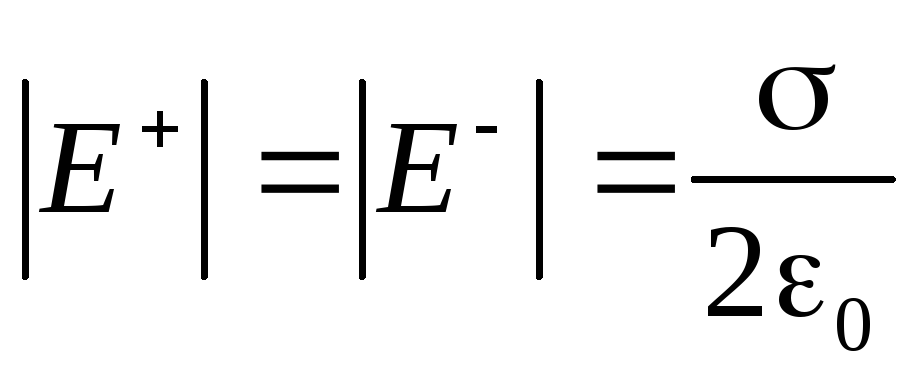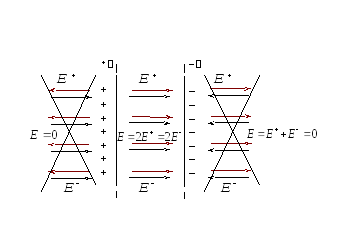
Fig. 2.9.

Pozitīvi uzlādēta plaknes jaudas līnijas ir vērstas uz plakni, kas ir negatīva. Kad šie lauki ir papildinājums, saspīlējums no rezultātā lauka ārpus kondensatora izrādās nulle, un iekšpusē kondensatoru, kur šie lauki sakrīt virzienā - lauks dubultojas:

. (2.17)

1. piemērs. Plāns, bezgalīgi garš pavediens ir jāmaksā viendabīgi ar lineāro uzlādes blīvumu λ . Atrast spriedzi elektrostatiskais lauks E.(r.) izlases veidā r. No pavediena.

Pieņemsim zīmējumu:

Analīze:

Jo Pavediens veic punkts, Piemērojiet di metodi. Izcelt bezgalīgi nelielu vadītāja garuma elementu dlkas satur maksu dq.=dlλ.. Aprēķiniet lauka intensitāti, ko rada katrs diriģenta elements patvaļīgā punktā no pavediena attālumā bet. Vector tiks novirzīts pa taisnu līniju, kas savieno punkta uzlādi ar novērošanas punktu. Iegūto lauku iegūst normāli uz pavedienu pa X asi. Ir nepieciešams atrast daudzumu de x.: de x \u003d.de.cosα. .

A-Priory:

.

Vērtība dl, r., mainiet konsekventi, mainot elementa stāvokli dl. Izteikt tos ar vērtību α:

kur dα. - bezgalīgi neliels leņķa α pieaugums, kā rezultātā rotācijas rādiusa-vektoram attiecībā pret punktu, kas pārvietojas uz pavedienu dl. Tad dl \u003d.r. 2 dα / A.. Pārvietojoties dl No punkta par leņķi svārstās no 0 0 līdz π / 2.

Līdz ar to .

Izmēra izmērs: [E] \u003d v / m \u003d kgm / mfm \u003d CLV / CLM \u003d V / m;

Atbilde:.

2. metode.

Saskaņā ar aksiālo simetriju maksas izplatīšanu, visi punkti atrodas vienādā attālumā no pavedieniem, ekvivalentu un intensitāte lauka tajās ir tas pats, ti.e. E.(r.) \u003d const, kur r.- attālums no novērošanas punkta uz pavedienu. Virziens E. Šajos punktos vienmēr sakrīt ar normāla virzienu uz pavedienu. Uz Gausa teorēmu; Kur Q.- Iespējams, ka virsma, caur kuru tiek aprēķināta plūsma, izvēlieties cilindra formā un veidojot vītni. Ņemot vērā, ka cilindra sānu virsma ir normāla, mēs iegūstam straumei:

T. K. K. K. K. E.\u003d const.

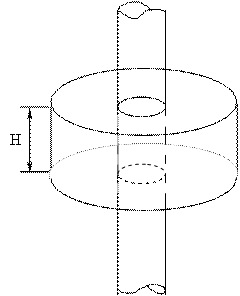
S. Bok.pov. \u003d. Uz2π .

No otras puses E.2ïan \u003d q / ε 0 ,

kur λn \u003d Q..

Atbilde:E.=λ /4πε 0 bet.

2. piemērs. . Aprēķiniet vienmērīgi uzlādētu bezgalīgu plaknes spriegumu ar virsmas blīvumu σ .

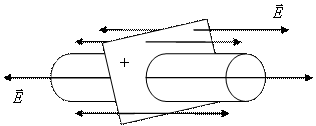
Spriegošanas līnijas ir perpendikulāri un vērsti abās plaknes pusēs. Kā slēgta virsma mēs izvēlamies cilindra virsmu, kuras pamatne ir paralēla plaknei, un cilindra ass ir perpendikulāra plaknē. Jo Veidojošie cilindri ir paralēli spriedzes līnijām (α \u003d 0, cos α \u003d 1 ), Šis plūsmas vektora stiprums caur sānu virsmu ir nulle, un pilnīga plūsma caur slēgtu cilindrisku virsmu ir vienāda ar plūsmas daudzumu caur tās bāzi. Maksa slēgta iekšpusē slēgtā virsma ir σ S. OSN. , tad:

F e \u003d 2 E.S. Vai f e \u003d \u003d, tad e \u003d \u003d \u003d

Atbilde:E \u003d, nav atkarīgs no cilindra garuma un jebkurā attālumā no plaknes, kas ir tāds pats modulī. Vienmērīgi uzlādēta plakne vienmērīgi.

3. piemērs. . Aprēķiniet divu bezgalīgi uzlādētu lidmašīnu lauku, ar virsmas blīvumu + Σ un -σ, attiecīgi.

E \u003d e \u003d 0; E \u003d E + + e - \u003d.

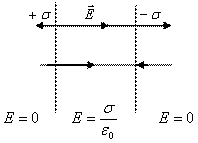
Atbilde: Rezultātā lauka stiprums reģionā starp lidmašīnām ir vienāds ar E \u003d, un ārpus tilpuma, ko ierobežo lidmašīnas, ir nulle.

4. piemērs. . Aprēķiniet lauka stiprumu vienmērīgi uzlādēts ar virsmas blīvumu maksas + σ sfēriskā virsma rādiusu R..

Tad, un

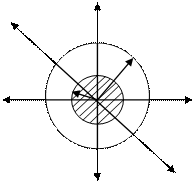
ja R.< R , то внутри замкнутой поверхности нет зарядов и электростатическое поле отсутствует (Е=0).

Atbilde:.

5. piemērs. . Aprēķiniet sprieguma skaļumu, kas uzlādēts ar lielapjoma blīvumu ρ , bumbu rādiuss R..

Slēgtās virsmas veidā ņemiet sfēru.

Ja r. ≥R. , tad \u003d 4πr 2 e; E \u003d.

ja R.< R , то сфера радиусом r., aptver maksu q "vienāds ar q" \u003d (kā izmaksas tiek uzskatītas par apjomiem, un apjomi, piemēram, rādiusu kubi)

Tad TGAUS

Atbilde:; Vienmērīgi uzlādēta trauka iekšpusē spriedze aug lineāri ar attālumu r.no viņa centra un ārpus tās - samazinās atpakaļ proporcionāli r. 2 .

6. piemērs. . Aprēķināt intensitāti lauka bezgalīgs, apaļais cilindrs uzlādēts ar lineāru uzlādes blīvumu λ , rādiuss R..

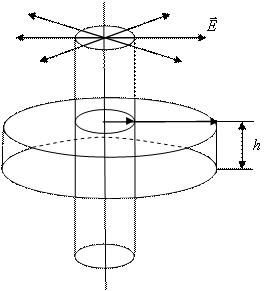
Thread vektora plūsma caur cilindra galiem ir 0, un caur sānu virsmu:

Jo vai,

tad (ja r\u003e r)

ja λ\u003e 0, Е\u003e 0, vektors ir vērsts no cilindra,

ja λ.< 0, Е < 0 , вектор Ē направлен к цилиндру.

Ja R.< R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е = 0

Atbilde: (R\u003e r); E \u003d 0 (R\u003e r). Iekšā vienmērīgi uzlādēts virs bezgalīgas, apaļas cilindra virsmas, nav lauka.

7. piemērs. . Elektrisko lauku izveidoja divas bezgalīgi garas paralēlas plaknes ar virsmas lādiņām 2 NKL / m 2 un 4ken / m 2. Nosakiet intensitāti lauka reģionos і, іі, іііііііііііn. Veidot atkarības grafiku Ē (r.) .

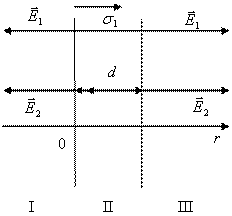
Lidmašīnas sadalīt vietu 3 jomās

Virziens Ē no tā izrietošais lauks uz vairāk.

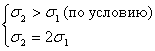
Projektā r.:

; «–»; ;

; «–»; ;

; «+»; .

Grafiks Ē (r.)

Izvēlieties skala: E. 2 =2 E. 1

E 1 \u003d 1; E 2 \u003d 2

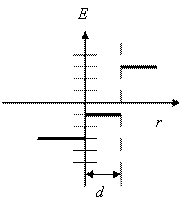
Atbilde:E. І \u003d -345 V / m; E. І i \u003d -172 v / m; E. І \u003d 345 V / m.

Numurs 8. . Ebonīta cietā bumba rādiuss R. \u003d 5 cm tiek uzlādēts, vienmērīgi sadalīts ar tilpuma blīvumu ρ \u003d 10 nl / m 3. Nosakiet elektrisko lauka stiprību punktos: 1) attālumā r. 1 \u003d 3 cm no sfēras centra; 2) uz sfēras virsmas; 3) attālumā r. 2 \u003d 10 cm no sfēras centra.

Apsveriet lauka, kas izveidots ar maksu, vienmērīgi sadalīts bezgalīgā pavediena. Mēs nolēmām šo uzdevumu pēdējā lekcijā, izmantojot elektrisko lauku superpozīcijas principu (sk. 1.11.).

Tagad mēs parādīsim, ka tas ir nedaudz vieglāk aprēķināt šo lauku, izmantojot Gauss teorēmu.

Noteikt lauka stiprumu attālumā r. No pavediena uzlādēts ar pastāvīgu lineāru blīvumu:

, [CL / m] (2.10)

Ap vītni ar slēgtu cilindrisku virsmu (2.7 att.). Cilindra augstums - h.un tās dibināšanas rādiuss - r..

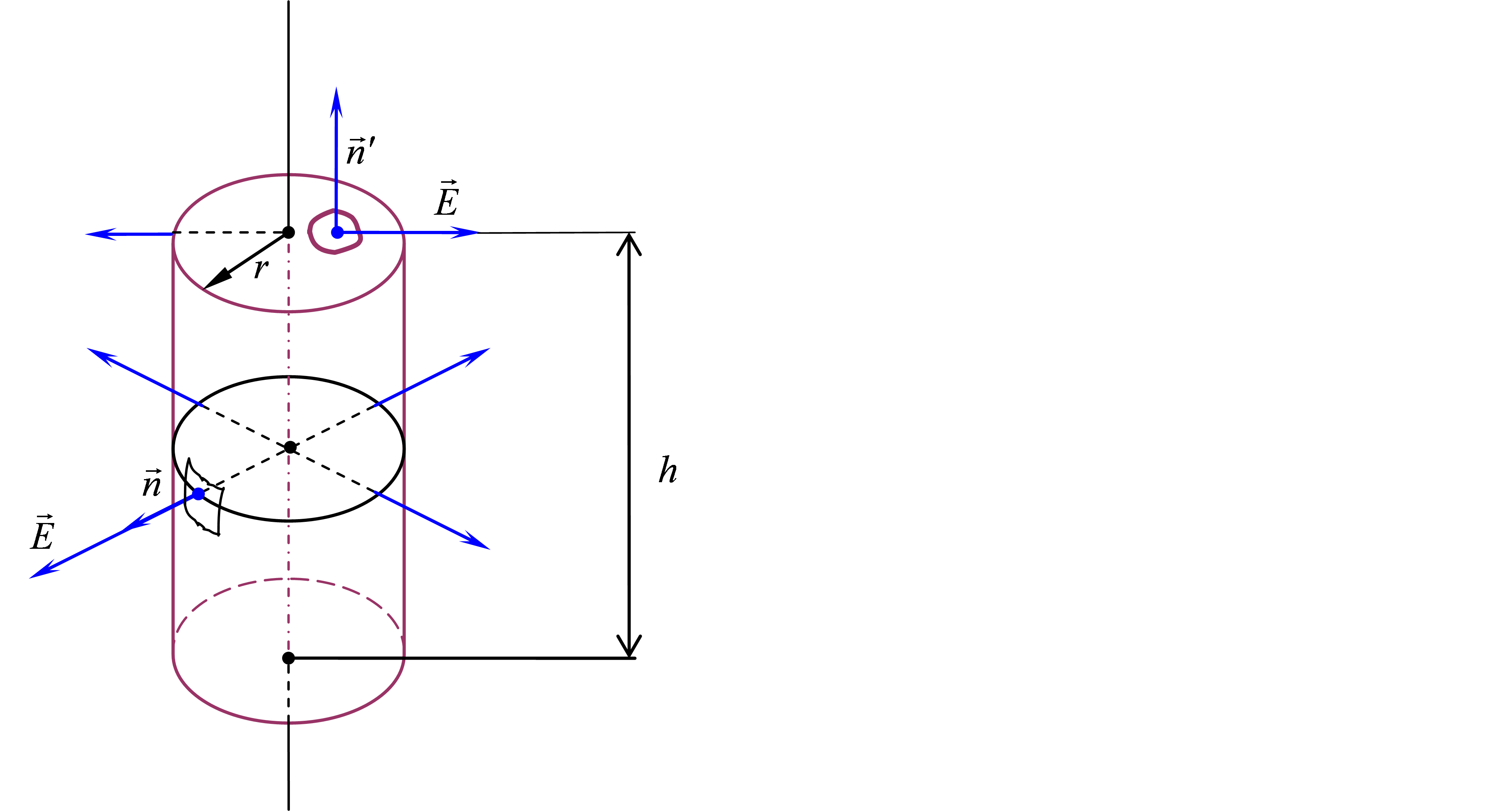
Lauks, ko rada uzlādētajam pavedienam, ir cilindrisks simetrija. Šajā sakarā sprieguma vektori visos balona sānu virsmas punktos būs vienāda ar moduli un ir vērsti radiāli, tas ir, perpendikulāri cilindra sānu virsmai. Uz cilindra bāzes vektori, kas vērsti uz to pašu radiāli, "slaidu", pamatojoties uz taisnu leņķi ar normālu.

Aprēķiniet vektora plūsmu caur izvēlētā cilindra virsmu. Pilna plūsma caur šo slēgto "Gaussian" virsmu ir izgatavota no plūsmas caur cilindra sānu virsmu un caur diviem pamatiem:

Pēdējie divi integrāli ir nulle, jo "bīdāmās" cilindra vektoru bāzēm nav iekļūstot un nerada straumi. Formāli šie divi integrāli ir nulle, jo starp vektoriem un taisnu leņķi un. Pa šo ceļu

Visos cilindra sānu virsmas punktos E. =E r. \u003d const un.

Tāpēc plūsma caur sānu virsmu cilindra ir vienāda

Tas ir plūsma elektriskā lauka stiprības vektora, ko aprēķina pēc plūsmas definīcijas.

Tagad mēs izmantojam Gauss Theorem, atzīmējot iepriekšējo lietu, ka "Charge ieslodzītais Gausa virsmas iekšpusē" šajā gadījumā ir koncentrēta uz pavediena stiepjas h. - uz cilindra ass:

Pa šo ceļu

(2.12)

No šejienes tagad ir viegli iepazīties ar mums hiperbolisku atkarību no intensitātes lauka no attāluma līdz pavedienam - r. (Sk 1.11).

1. Infinīta vienmērīgi uzlādēta plakne. Flat kondensatora lauks

Ļaujiet elektriskajam laukam izveidot ar maksu, vienmērīgi sadalīti pa infinīta plaknes virsmu, ar virsmas blīvumu s (2.8. Att.)

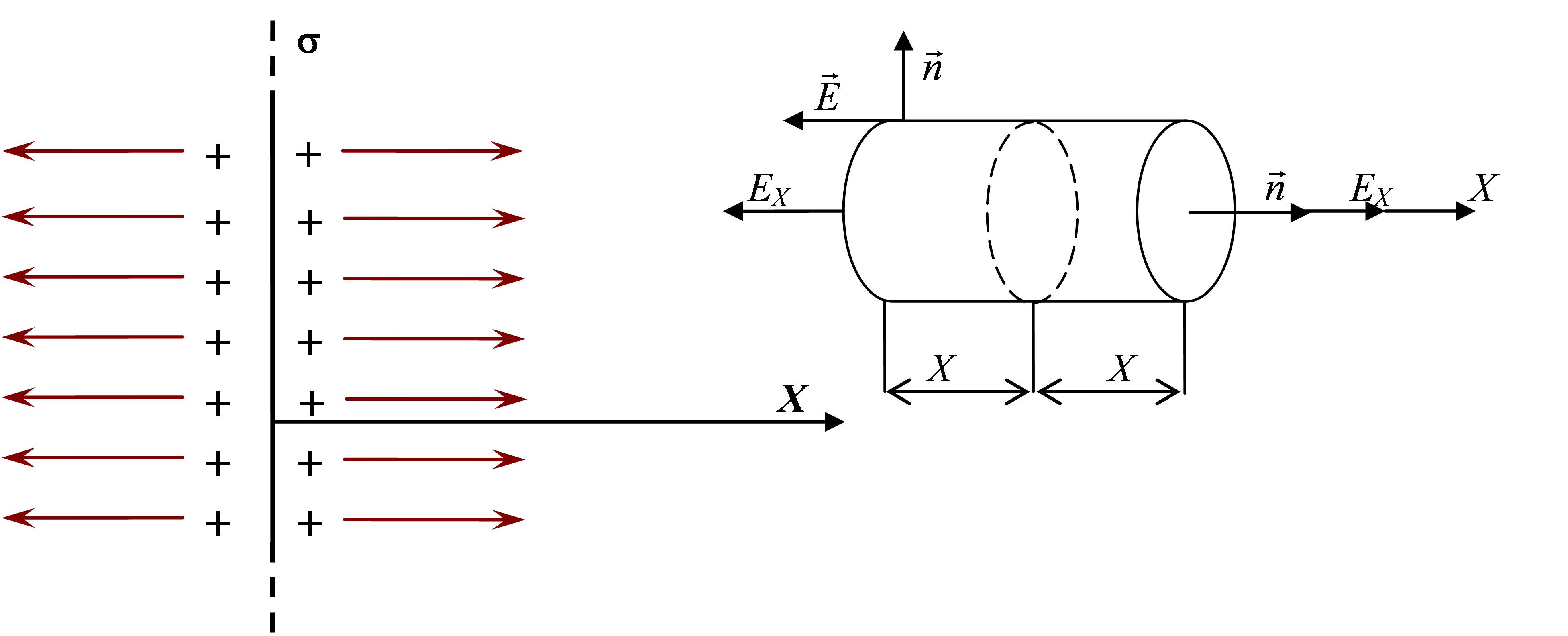
No uzdevuma simetrijas izriet, ka lauks tiek nosūtīts visur perpendikulāri virsmai. Mēs uzzinām, kā lauka stiprums mainās, jo tas noņem no uzlādētās lidmašīnas.

Kā Gausa virsma ir ērti izvēlēties cilindru. Cilindra ass nosūtīs perpendikulāra lidmašīnu, tā pamatne atrodas attālumā H. Simetriski abās virsmas pusēs.

Aprēķiniet sprieguma vektora stiprumu caur cilindra sānu virsmu un pamatni. Šādi no att. 2.8., Stroy vektora plūsma caur cilindra sānu virsmu ir nulle, jo šeit spriedzes vektori "slide" uz virsmas un.

Tad pilnu plūsmu caur slēgtu cilindrisku virsmu var rakstīt kā plūsmu caur diviem cilindra bāzēm.

Tā ir vērtība, kas aprēķināta, lai noteiktu plūsmu.

Tagad mēs izmantojam Gauss Theorem, atzīmējot, ka maksa q., "Atrodas iekšpusē Gausa virsmas", šajā gadījumā koncentrējas uz vietni S. = S. OSN, "samazināt" cilindru bezgalīgas plaknes

Mēs apvienojam rezultātus (2.15) un (2.14) Gausa vienādojumam:

Kur seko

Produkcija. Lauks, ko rada bezgalīga vienmērīgi uzlādēta plakne, vienmērīgi. Tas nemainās ar attālumu no uzlādētās virsmas, ne virzienā.

Tagad apsveriet vēl vienu svarīgu piemēru. Ļaujiet laukam izveidot divas bezgalīgas lidmašīnas, kas jāmaksā savādāk, bet ar tādu pašu lielumu uzlādes blīvuma (2.9 att.). Tā ir svarīga elektrostatikas idealizācija - dzīvoklis kondensators. Katrs šī kondensatora atpūtas laiks rada viendabīgu lauku, kuras spriedze, no kuras mēs tikko instalējām (2.16):

.

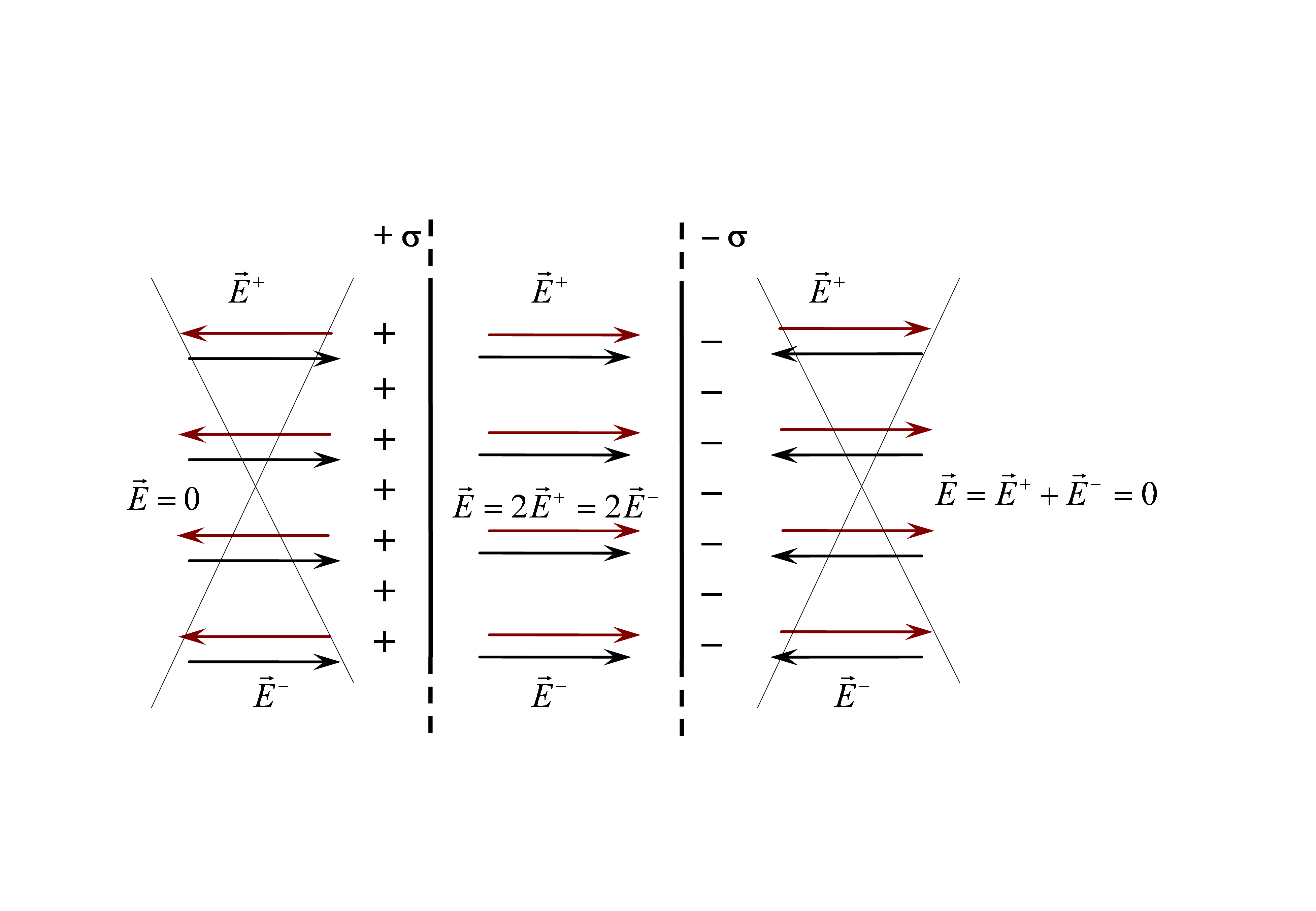
Pozitīvi uzlādēta plaknes jaudas līnijas ir vērstas uz plakni, kas ir negatīva. Papildus šīm jomām, saspiegums no rezultātā lauka ārpus kondensatora izrādās nulle, un iekšpusē kondensators, kur šie lauki sakrīt virzienā, lauks dubultojas.