Elektromagnētisms
9. nodaļa. Elektriskais lauks vakuumā
Lauka spriedze
Tika eksperimentāli konstatēts, ka daļiņas var rasties mijiedarbība ir daudz spēcīgāka par smagumu. Izskaidrot šo masu m. Daļiņas pievienoja vēl vienu daļiņu raksturojumu - elektriskais lādiņš q.mēra ar coulins (Cl).
Zvanīsim par uzlādētu daļiņu, ti., daļiņu ar maksu q., punkts q. (Atšķirībā no iekasētā iestāde, kuru izmēri nevar tikt atstāti novārtā saskaņā ar šī uzdevuma nosacījumiem). Katrs fiksētā maksas punkts q. Rada apkārtējo telpu elektriskais lauks (Precīzāk elektrostatiskais lauks). Jebkurā citā brīdī šajā jomā darbosies elektroenerģija :
kur tiek saukts par vektoru spriedze elektriskais lauks Punktā, kur ir maksa. Jauda var tikt novirzīta vai jāmaksā q. vai no viņa. Šajā sakarā divu veidu maksas ieviests: pozitīvs un negatīvs. MultiMame maksājumi tiek piesaistīti, un tie paši nosaukumi tiek repelēti viens no otra (31.1. Att.).

Ticība tiek noteikta kā spēks, kas darbojas ar vienu pozitīvu punktu, šajā brīdī:
kur\u003e 0. No izteiksmes (31.2) var redzēt, ka dimensija ir Ņūtona uz kulonu (n / cl).
Pieredze rāda, ka kustības punktu maksa q. Rada attālumu r. No viņa spriedzes
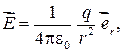 (31.3)
(31.3)
kur ε 0 ir elektriskā konstante (ε 0 \u003d 8,85 · 10-12 kl 2 / (n · m 2)), - viens vektors no rādiusa vektora, kas pavadīts lauka centrā, kas novietots koordinātu sākumā kurā atrodas brīdinājuma maksa q., Pirms jūs interesē lauka punkts.
No izteiksmes (31.1) var redzēt, ka elektriskais spēks, kas darbojas uz maksas, ir vērsta, kā arī vektors, ja maksa ir pozitīva, un pretējs vektors, ja maksa ir negatīva (31.2. Att.).
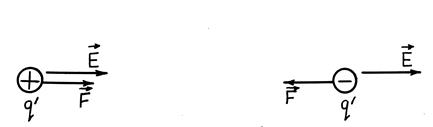
No pieredzes izriet, ka sistēmas lauka stiprums N. Fiksētie punkti
kur - lauka stiprums, kas jūs interesē, izveidots i.- punktu maksa, ja nav citu punktu nodevu. Attiecība (31.4) izsaka elektrisko lauku superpozīcijas princips.
31.1. Piemērs. Divas bumbiņas ar masām 0,3 kg ir tādā attālumā, ka to maksājumu mijiedarbība ir līdzsvarota ar gravitācijas piesaistes spēku. Atrodiet bumbiņu rādiusus, ja bumbiņu bumbas virsmas blīvums ![]()
| Ņemot vērā: m. 1 = m. 2 = m.\u003d 0,3 kg F. E \u003d F. G. R. 1 = R. 2 = R. | Lēmums 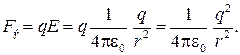
|
||||
| R. – ? |
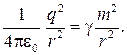
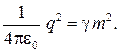
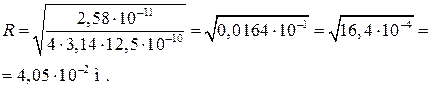
Atbilde:R.\u003d 4 cm.
31.2. Piemērs. Punktu nodevas q. 1 = 2q. un q. 2 = – q. Atrodas, kā parādīts attēlā. 31.4. Attālums starp maksām ir vienāds d.. Noteikt kādā attālumā x. 1 no maksas q. 1 Elektriskā lauka stiprums ir nulle.
| Ņemot vērā: q. 1 = 2q. q. 2 = – q. d. E ( x. 1) = 0 | Lēmums 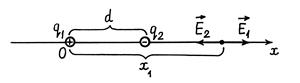 Fig. 31.3. Fig. 31.3. |
| x. 1 – ? |
Saskaņā ar elektrisko lauku superpozīcijas principu vietā, kur jāveic nosacījums
![]()
kur un - maksājumu radīto maksājumu spriedze q. 1 I. q. 2. Šajā brīdī. Acīmredzot šis stāvoklis netiks veikts ārpus ass x. (Vektori un režisors leņķī viens otram), kā arī uz ass x. Pa kreisi no maksas q. 1, kur vienmēr E. 1 > E. 2 (sk formula (31.3) un nosacījumu uzdevuma). Starp apsūdzībām uz ass x. Tas nevar būt nulle, jo vektori ir vērsti vienā virzienā. Joprojām pieņem, ka vēlamais punkts atrodas uz ass x. Tieši no maksas q. 2 (sk. 31.3. Att.). Attālums x. 1 no maksas q. 1 Atrodiet no stāvokļa
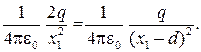
Spere un ekstrakts sakņu laukumu no kreisās un labās vienlīdzīgas daļas:
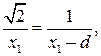
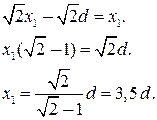
Atbilde: x. 1 = 3,5 d..
§ 32. Vector plūsma
Viscable lauka vektors, kas attēlots, izmantojot līnijas vektors , kam seko šādi:
1) Tieši tiem katrā brīdī sakrīt ar vektora virzienu;
2) līniju skaits, kas iekļūst virsmas laukuma vienībā, perpendikulārās līnijas (līnijas biezums), ir vienāda ar vektora moduli (32.1. Att.).
Elektriskais lauks Piezvanīt vienveidīgsJa katrā lauka vektora punktā \u003d const. Šādas lauka vektoru līnijas ir paralēlas, un attālums starp tiem ir vienādi (32.2. Att.).
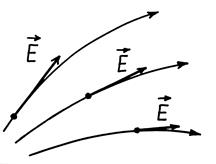
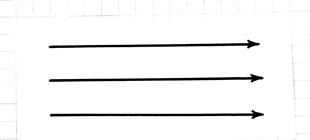
Fig. 32.1. 32.2.
Līnijas vektors elektrostatiskais lauks Sāciet ar pozitīviem maksājumiem un beidzas ar negatīviem maksājumiem.
Veikt pamatplatformu ds. Vektora laukā (32.3. Att.). Ļaujiet - viena normāla vektoram uz vietni ds., α ir leņķis starp vektoriem un. Tad līniju vektoru skaits iekļūst ds.labi
![]()
kur - vektors, kura modulis ir vienāds ds.un virziens sakrīt ar vienu normālu vektoru uz vietni ds..

Nosaukt flow f vektorscaur patvaļīgu virsmu S. Vector līniju skaits, kas iekļauj šo virsmu. Acīmredzami
integrāli uz virsmas S. No vektoru skalāra produkta un. Plūsma - algebriskā vērtība. Plūsmas zīme ir atkarīga no parastā virziena izvēles līdz ds.. Slēgtām virsmām ir ierasts veikt ārējo normālu.
§ 33. Gauss teorēma par vektora lauku
Teorēma. Vector plūsma caur jebkuru slēgtu virsmu S. Velns q. vn. / ε 0, kur q. vn. - Algebriskā maksu apjoms šajā virsmā:
![]() (33.1)
(33.1)
ja neatņemama aplis nozīmē, ka integrācija tiek veikta pa slēgtu virsmu.
Thorem pierādījums. Apsveriet vienas fiksētās elektrisko lauku punkts q.. Ļaut būt q. \u003e 0. Garīgi ap minimumu q. patvaļīga slēgta virsma S. (33.1. Att.).
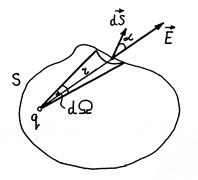
Mēs atrodam plūsmu d.F vektors caur elementu ds. Virsmas. Acīmredzami

kur ![]() - pamatskola (telpiskais) leņķis konusā, pamatojoties uz ds., ar virsotni pie maksas punkta q..
- pamatskola (telpiskais) leņķis konusā, pamatojoties uz ds., ar virsotni pie maksas punkta q..
Vector plūsma caur visu slēgto virsmu S.
kur ir pilna ķermeņa stūra. Mēs saņēmām
kas sakrīt ar izteiksmi (33.1).
Tagad apsveriet sistēmas radīto elektrisko lauku N. Fiksētie punkti Maksājumi, kas garīgi ap šo maksas sistēmu par patvaļīgu slēgto virsmu S.. Izmantojot elektrisko lauku superpozīcijas principu, mēs varam rakstīt
![]()
kur q. - algebriskā summa N. Maksa, kas sakrīt ar izteiksmi (33.1).
Gauss Theorem ļauj dažos gadījumos ļoti viegli noteikt spriedzi jebkurā elektriskā lauka punktā.
33.1. Piemērs. Mums ir bezgalīga vienmērīgi uzlādēta plakne ar virsmas blīvums Maksa σ. Noteikt intensīvu parst E. x. No plaknes.
Mēs tērēsim caur Gausa interesējošo jautājumu mums S. Simetriskā veidā attiecībā pret cilindra plakni tā, ka punkts ir uz cilindra pamatnes (32.2. Att.). Mēs atradīsim vektora plūsmu caur Gausa virsmu:
kur S. OSN. - cilindra pamatgase. Integrējot, mēs uzzinājām, ka vektora plūsma caur cilindra sānu virsmu ir nulle (vektoru līnijas nespēlē šo virsmu) un visiem cilindra bāzes punktiem α \u003d 0 un E. \u003d const.
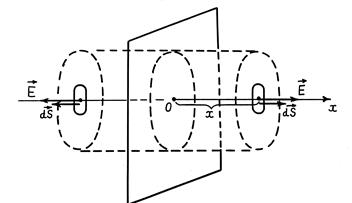
Saskaņā ar teorēmu Gauss
kur - maksa par plakni koncentrējas uz cilindra iekšpusē. Atrodi viņu. Pēc definīcijas, virsmas blīvums
Gadījumā, ja vienādi uzlādēta plakne (σ \u003d const), mēs varam rakstīt
(no 33.2. Att.) Ir redzams, ka maksa ir koncentrēta uz daļu no plaknes ar platību S. Pieder), no kurienes
![]() (33.4)
(33.4)
Izteikt izteiksmes (33.2) un (33.4) attiecību (33.3), mēs saņemam

No izteiksmes (33.5) to var redzēt E. atkarīgs no attāluma x. no uzlādes lidmašīnas, t.e.
Līdz ar to elektriskais lauks, ko rada bezgalīgi uzlādēta plakne, ir vienāda.
33.2. Piemērs. Mums ir vienmērīgi uzlādēta sfēra ar uzlādes virsmas blīvumu Σ. Sfēras rādiuss R.. Noteikt intensīvu parst E. Elektriskais lauks attālumā r. no sfēras centra.
(No 33. punkta var redzēt, tad Gausa virsmas iekšpusē nav jāmaksā), no kurienes tas izriet, ka
Līdz ar to iekasētā sfēras spriedzes laikā E. Elektriskais lauks ir nulle.
Tagad definējiet E. Punktā ārpus uzlādētās sfēras ( r.> R.). Ļaujiet sfērai pozitīvi apsūdzēt. Sakarā ar simetriju. Vector E. Lauki, ko rada sfēra, tādā brīdī jūs interesē radiāli no sfēras centra.
E. \u003d const.
Saskaņā ar teorēmu Gauss
No attēla. 33.3. Var redzēt, ka iekasētā sfēra ir iekšpusē Gausa virsmas un tā ir maksa q. vn. vienāds ar uzlādi q. Sf. sfēras. Vienmērīgi uzlādēta sfēra (σ \u003d const), mēs varam ierakstīt

![]() (33.8)
(33.8)
Izteikšanās aizstāšana (33.6) un (33.8) līdz attiecībai (33.7), mēs saņemam
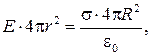
Līdz ar to, spriedze E. Lauki ārpus uzlādes sfēras samazinās ar attālumu r.. Grafiski atkarība E.(r.) Vienveidīgi iekasētā sfēras elektriskais lauks ir atspoguļots 1. attēlā. 33.4.

33.3. Piemērs. Mums ir vienmērīgi uzlādēta bumba ar lielapjoma blīvumu maksas ρ. Bumbu rādiuss R.. Noteikt intensīvu parst E. Elektriskais lauks attālumā r. No bumbas centra.
Integrējot, mēs to ņēmām, ka visiem punktiem Gausa sfēra α \u003d 0 un E. \u003d const.
Saskaņā ar teorēmu Gauss
kur - lādiņa par daļu no bumbu, kas vērsta iekšpusē Gausa sfērā. Atrodi viņu. Pēc definīcijas, lielapjoma blīvums maksas
Vienmērīgi uzlādēta bļoda (ρ \u003d const), mēs varam rakstīt
kur - bumbas apjoms Gausa sfērā. No izteiksmes (33.12) mēs atrodam
![]() (33.13)
(33.13)
Izteikšanās (33.10) un (33.13) attiecība (33.11), mēs saņemam
Ja telpā ap elektrisko lādiņu, veikt citu maksu, tad Coulomb Force darbosies uz to; Tātad, telpā, kas atrodas apkārtējos elektriskos maksājumus, pastāv spēka lauks. Saskaņā ar mūsdienu fizikas idejām lauks patiešām pastāv un kopā ar vielu ir viena no materiāla esamības formām, ar kurām tiek veikta konkrēta mijiedarbība starp makroskopiskām struktūrām vai daļiņām, kas ir vielas daļa. Šajā gadījumā viņi saka, ka elektriskais lauks - lauks, ar kuru elektriskās maksas mijiedarbojas. Mēs uzskatām, elektriskās jomas, kas tiek izveidotas ar fiksētiem elektriskajiem maksājumiem un tiek saukti elektrostatisks.
Lai atklātu un piedzīvotu elektrostatisko lauku testa punkts pozitīva maksa - Šāda maksa, kas neizkropļo pētījuma laukumu (nerada lauka radīto maksu pārdali). Ja maksas laukā Q, Novietojiet izmēģinājuma maksu Q. 0, tad ir jauda F., atšķiras dažādos jomās, kas, saskaņā ar likumu par Coulon, ir proporcionāls izmēģinājuma maksas Q. 0. Tāpēc attiecība f / Q. 0 nav atkarīga Q. 0 un raksturo elektrostatisko lauku tajā vietā, kur atrodas izmēģinājuma maksa. Šo vērtību sauc par spriedzi un ir elektrostatiskā lauka jaudas raksturojums.
Elektrostatiskā lauka spriedze Šajā brīdī ir fiziskais daudzumsar spēku, kas rīkojas ar izmēģinājuma vienotu pozitīvu uzlādi, kas ievietots šajā jomā:
Punkts dot maksas lauka spriedze vakuumā

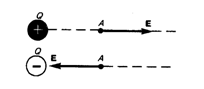 Vector E virziens sakrīt ar spēka virzienu, kas darbojas ar pozitīvu maksu. Ja lauks ir izveidots ar pozitīvu maksu, vektors e ir vērsta pa rādiusu-vektoru no maksas Ārējā telpa (Pozitīva uzlāde); Ja lauks ir izveidots negatīva maksa, tad vektors e ir vērsta uz maksu (att.).
Vector E virziens sakrīt ar spēka virzienu, kas darbojas ar pozitīvu maksu. Ja lauks ir izveidots ar pozitīvu maksu, vektors e ir vērsta pa rādiusu-vektoru no maksas Ārējā telpa (Pozitīva uzlāde); Ja lauks ir izveidots negatīva maksa, tad vektors e ir vērsta uz maksu (att.).
Elektrostatiskā lauka sprieguma vienība - Newton uz kulonu (N / CL): 1 N / Cl - šī lauka intensitāte, kas līdz brīdim uzlādēt 1 CL iedarbojas ar spēku 1 h; 1 N / cl \u003d 1 V / m, kur (volti) ir elektrostatiskās lauka potenciāla vienība. Grafiski elektrostatiskais lauks tiek attēlots, izmantojot spriedzes līnijas - Līnijas pieskares, uz kurām katrā brīdī sakrīt ar vektora e (att.).
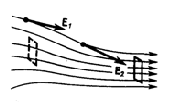 Tā kā katrā konkrētā vietā spriedzes vektoram ir tikai viens virziens, tad spriedzes līnija nekad krustojas. Priekš vienota lauks (Ja spriedzes vektors jebkurā brīdī ir pastāvīgs lieluma un virziena) intensitātes līnija paralēli sprieguma vektoram. Ja lauks tiek izveidots ar punktu uzlādē, spriedzes līnija ir radiāla taisna, kas ir no maksas, ja tas ir pozitīvs (att. bet), un tajā iekļauj, ja maksa ir negatīva (att. b.). Lielās skaidrības dēļ elektrostatiskā lauka attēlošanas grafiskā metode tiek plaši izmantota elektrotehnikā.
Tā kā katrā konkrētā vietā spriedzes vektoram ir tikai viens virziens, tad spriedzes līnija nekad krustojas. Priekš vienota lauks (Ja spriedzes vektors jebkurā brīdī ir pastāvīgs lieluma un virziena) intensitātes līnija paralēli sprieguma vektoram. Ja lauks tiek izveidots ar punktu uzlādē, spriedzes līnija ir radiāla taisna, kas ir no maksas, ja tas ir pozitīvs (att. bet), un tajā iekļauj, ja maksa ir negatīva (att. b.). Lielās skaidrības dēļ elektrostatiskā lauka attēlošanas grafiskā metode tiek plaši izmantota elektrotehnikā.
Lai izmantotu spriedzes līnijas, ne tikai virzienu, bet arī elektrostatiskā lauka spēka vērtību, tika panākta vienošanās tos veikt ar noteiktu blīvu blīvu: sprieguma līniju skaitu, kas pārņem virsmas laukuma vienību, perpendikulāri intensitātes līnijām , jābūt vienādam ar E. vektoru, tad spriedzes līniju skaits, kas iekļūst pamatplatformā d S, normāls n. kas veido leņķi ar vektoru E.labi E.d. S cos.a. \u003d E n.d. S, Kur E P.-Products vektors E. Normāli n. Tiesai D. S.(Att.).
 DF E \u003d E N DS \u003d vērtība \u003d E.ds sauc plūsmas vektora intensitāte caur platformu D. S. Šeit D. S. \u003d D. S.n. - vektors, kura modulis ir d S, Un virziens sakrīt ar normālas virzienu n. Uz vietni. Virziena vektora izvēle n. (un tāpēc S.Tas ir nosacīts, jo to var novirzīt uz jebkuru pusi. Elektrostatiskās lauka intensitātes plūsmas vienība - 1 V × m.
DF E \u003d E N DS \u003d vērtība \u003d E.ds sauc plūsmas vektora intensitāte caur platformu D. S. Šeit D. S. \u003d D. S.n. - vektors, kura modulis ir d S, Un virziens sakrīt ar normālas virzienu n. Uz vietni. Virziena vektora izvēle n. (un tāpēc S.Tas ir nosacīts, jo to var novirzīt uz jebkuru pusi. Elektrostatiskās lauka intensitātes plūsmas vienība - 1 V × m.
Par patvaļīgu slēgto virsmu S. Plūsma vektors E. Caur šo virsmu
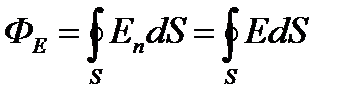 ,
,
kur integrācija tiek uzņemta uz slēgtas virsmas S. Plūsma vektors E. ir algebriskā vērtība: Atkarīgs ne tikai uz lauka konfigurāciju E., bet arī no virziena izvēles n.. Slēgtām virsmām parasto pozitīvo virzienu ārējais normāls I.E. Normāls režisors ārpus teritorijas, uz kuru pārklāts ar virsmu.
Spēku neatkarības princips ir piemērojams Coulomb Forces, tas ir, no tā izrietošais spēks f, kas darbojas lauka pusē uz testa maksas Q 0, ir vienāds ar to, ka to piemēro to spēku vektoru summu katrs no Qi maksas. F \u003d q 0 e un f i \u003d q 0 e i, kur e-spriedze no rezultātā lauka, un E i ir lauka spēks, ko rada maksas Q i. Aizvietojot to iepriekš minētajā izteiksmē, mēs saņemam. Šī formula izsaka elektrostatisko lauku superpozīcijas (uzlikšanas) principu, saskaņā ar kuru rezultātā radītā lauka intensitāte ir vienāda ar šajā punktā izveidoto lauka spriedzes ģeometrisko summu katrā no maksām atsevišķi.
Superpozīcijas princips ir piemērojams, lai aprēķinātu elektrostatisko jomu elektrisko dipolu. Elektriskā dipola sistēma ir divu vienāda moduļa multi-dimensiju nodevu (+ Q, -Q), attālums l, kas ir ievērojami mazāks par attālumu līdz attiecīgajiem punktiem. Saskaņā ar superpozīcijas principu, dipola lauka spriedzi patvaļīgā punktā ![]() kur e + un elastīgo spriedzi laukiem, ko rada attiecīgi pozitīvas un negatīvas maksas.
kur e + un elastīgo spriedzi laukiem, ko rada attiecīgi pozitīvas un negatīvas maksas.
Katra elektriskā lādiņa ieskauj elektrisko lauku. Ilgtermiņa pētījumu rezultātā ārsta zinātnieki nonāca pie secinājuma, ka iekasēto struktūru mijiedarbība ir saistīta ar elektriskajiem laukiem, citiem. Tie ir īpašs jautājums, kas ir nesaraujami saistīta ar katru elektriskais lādiņš.
Elektriskā lauka pētījums tiek veikts, ieviešot nelielas uzlādes iestādes tajā. Šie uzņēmumi izsauc "izmēģinājuma maksas". Piemēram, bieži kā izmēģinājuma maksa tiek izmantota ar uzlādētu korķa bumbu.
Veicot testa maksu par elektrisko virsbūves lauku, kam ir pozitīva maksa, kas ir pozitīvi uzlādēts korķa bumba saskaņā ar tās rīcību novirzīsies, jo tuvāk mēs to nodrošināsim ķermenim.
Pārvietojot testa maksu par patvaļīgas uzlādes ķermeņa elektrisko lauku, to var viegli noteikt, ka spēks, kas darbojas uz tā, būs atšķirīga dažādās vietās.
Tādējādi, ja to novieto secīgi vienā vietā, kurā ir redzami testa pozitīvie maksājumi Q1, Q2, Q3, ..., QN var atrast, ka spēki, kas iedarbojas uz tiem, F1, F2, F3, .. ., Fn ir atšķirīgs, bet spēka attiecība lieluma noteiktu maksu par šādu jomu, ir konsekventi:
F1 / Q1 \u003d F2 / Q2 \u003d F3 / Q3 \u003d ... \u003d Fn / QN.
Ja mēs izskatīsim dažādus lauka punktus šādā veidā, tad mēs iegūstam šādu secinājumu: katram atsevišķajam punktam elektriskā laukā, attiecība par spēku, kas darbojas uz testa maksu, līdz šādas maksas lielumam ir vienmēr un neatkarīgi no vērtības izmēģinājuma maksas.
No tā izriet, ka šīs attiecības lielums raksturo elektrisko lauku patvaļīgā punktā. Vērtība, ko mēra ar spēka attiecību, kas darbojas pozitīvā uzlādē, atrodas šajā lauka punktā, uz maksas lielumu un ir elektriskā lauka stiprums:
Tas ir, kā redzams no tās definīcijas, ir vienāds ar spēku, kas darbojas uz vienību pozitīvu uzlādē, kas atrodas konkrētā jomā lauka.
Aiz elektriskās stiprības vienības ņem lielumu viena elektrostatiskā vienība ar spēku vienā Diena. Šādu vienību sauc par absolūtu elektrostatisko spriedzi.
Lai noteiktu jebkura punkta uzlādes elektriskās jomas spēku Q, kas patvaļīgi ir šīs maksas lauka, kas no tā atšķiras attālumā R1, tas ir nepieciešams, lai pārbaudes maksa Q1 šajā patvaļīgajā punktā un aprēķināt Fa spēku, kas darbojas uz tā (vakuumam).
FA \u003d (Q1Q) / R²₁.
Ja mēs ņemam attiecību par spēka daudzuma, kas ietekmē maksu, tās vērtības Q1, tad aprēķināšana spriedzi elektrotru cauruli pie A punktā:
Turklāt jūs varat atrast spriedzi patvaļīgā punktā; Tas būs vienāds ar:
Tādēļ spriedze elektriskā lauka punkta uzlādes noteiktā jomā (vakuumā) būs tieši proporcionāla lielumam šo maksu un apgriezti proporcionāls kvadrātu attāluma starp šo maksu un punktu.
Lauka spēks darbojas kā tas klusuma īpašības. Zinot to patvaļīgā lauka vietā E, ir viegli aprēķināt un stiprināt F, kas ietekmē q šajā brīdī:
Lauki - virziens spriedzes katrā konkrētā lauka punktā tiks apvienota ar spēka virzienu, kas darbojas ar pozitīvu maksu, kas ievietots punktā.
Ja lauku veido vairāki maksājumi: Q1 un Q2 - intensitāte E jebkurā brīdī, un šis lauks būs vienāds ar ģeometrisko summu E1 un E2 spriedzi, kas izveidota šajā punktā atsevišķi ar maksājumiem Q1 un Q2.
Elektriskā lauka izturība pie patvaļīgas punkta var attēlot grafiski, izmantojot virziena segmentu, kas nāk no šī punkta, līdzīgi kā spēka un citu vektoru daudzumu tēlu.




