Vairākās vispārējās fizikas kursa sadaļās tiek uzskatītas par vektoru laukiem (piemēram, elektrostatiskais lauks, magnētiskais lauks).

Vector plūsmas jēdzienu bieži izmanto šādu lauku trūkumu. Ras-Look šo koncepciju.

Ļaujiet tur būt elektriskais lauks dažās telpās telpā. Šajā laukā izvēlieties elementāru platformu. ds.. Ļaujiet normāli uz šo vietni n. Veido leņķi  ar elektrisko lauka stiprības vektoru (Vector modulis n. = 1).

Elektriskā lauka sprieguma plūsma caur šo platformu sauc par vērtību, kas ir vienāda ar

kur df - spriedzes vektora elementārā plūsma, \\ t E. - vektoru intensitātes vektors bezgalīgi nelielā platībā d.s. .

Kompozīcija En Tas ir skalārs, tāpēc stiprības vektora plūsma ir skalāra vērtība.

Dažreiz darbs n. ds. Aizstāts ar vektoru d.s. kas ir vērsta perpendikulāri vietnes plaknei; Moduļa vektors ds. vienāds ar elementārās platformas teritoriju.

Spēka stiprums caur galīgo zonu s. Velns

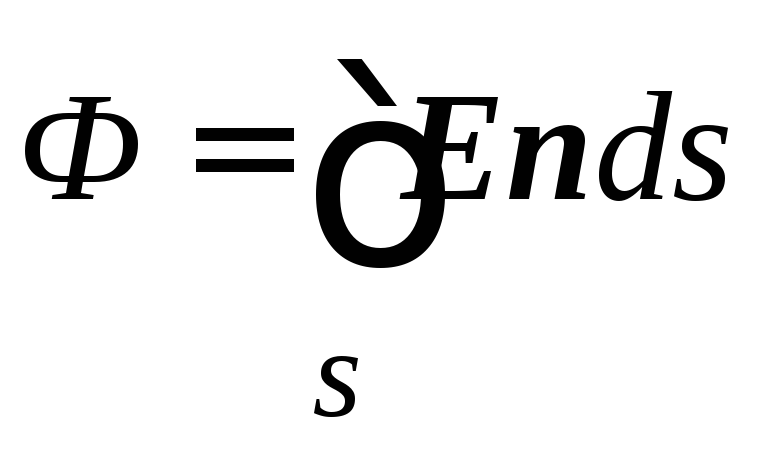Atkarībā no stūra vērtības starp normālu uz vietu un vektoru E. Plūsma var būt pozitīva un negatīva. Ja leņķis starp vektoriem E. un n. Akūta, tad plūsma ir pozitīva, ja stulba ir negatīva.

Ņemiet vērā, ka vektora virziens n. Tas ir izvēlēts pirms problēmas risināšanas patvaļīgi (perpendikulāri virsmai var nosūtīt uz divām savstarpēji pretējām pusēm). Tāpēc sprieguma vektoru plūsmas zīme nosaka pēc vektora virziena izvēle. n.

Ja virsma ir aizvērta, sprieguma vektora stiprums ir vienāds

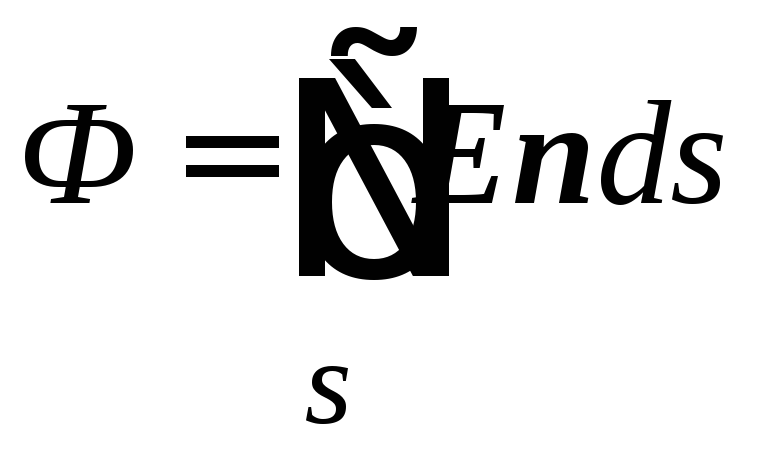i.e. integrāls tiek ņemts uz slēgta virsma s..

Šādā gadījumā vektors ir ierasts n. no virsmas. Šādā gadījumā plūsma caur slēgtu virsmu ir pozitīva, ja kopsavilkuma maksaslēgta virsma ir pozitīva.

Spriedzes stiprības dimensija [f] \u003d c. M \u003d n. m 2 / cl.

1.6. Teorēma Gaussa

Gausa teorēma ir galvenais elektrostatikas teorēma. Tā izveido saikni starp sprieguma vektora plūsmu caur slēgto virsmu un kopējo maksu, uz kuru attiecas šī virsma.

Apsveriet šo teoriju.

Ļaujiet elektriskajam laukam izveidot pozitīvu punktu maksu q..

Atrodiet elektriskā lauka stiprības vektora plūsmu caur slēgtu virsmu, kas aptver šo maksu.

Kā virsmu, izvēlieties rādiusa sfēru r.Kuru centrs sakrīt ar maksu q..

Kopš maksas, kas rada lauku, ir pozitīvs un atbrīvots no sfēras centrā, leņķis starp vektoru E. un vektors n. Visos virsmas punktos ir nulle.

Tāpēc stiprums sprieguma vektoru starpniecību pamatskolas virsmu ds. būs vienāds En. ds. = E.cos. ds. = E.cos0. ds. = EDS.

Citiem vārdiem sakot, situācijā aplūkotais scalar produkts sprieguma vektora elektrostatiskais lauks Uz Armēnijas elementārās virsmas vektora, šo plakstiņu moduļu produkts.

No lauka, ko rada čehu maksas intensitāte ir vienāda ar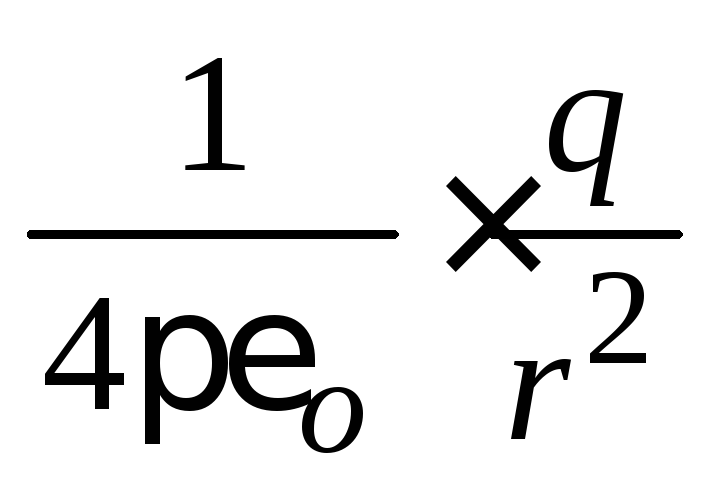

.

Tā kā maksa atrodas sfēriskās virsmas centrā, attālums no maksas uz virsmu visos tās punktos ir vienādi un vienādi r.. Līdz ar to sprieguma vektoru modulis visos sfēriskās virsmas punktos ir tāds pats: E. \u003d const.

Konstanti var izņemt neatņemama zīmei, tāpēc sprieguma vektora stiprums caur slēgtu virsmu šajā gadījumā ir vienāds ar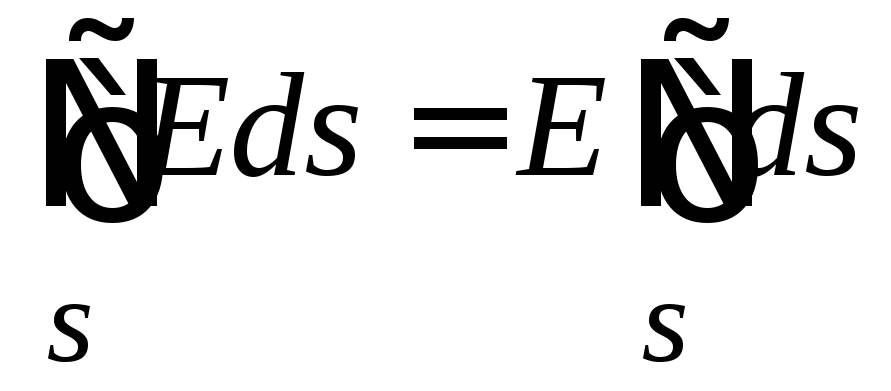

.

Integral no elementārās virsmas laukuma s.pārņēmis visu virsmu ir vienāda ar platību šīs virsmas. s.. Šādā gadījumā virsma ir sfēra, kuras teritorija s. \u003d 4. r. 2 .

Tādējādi sprieguma vektora plūsma caur slēgtu virsmu šajā gadījumā ir vienāds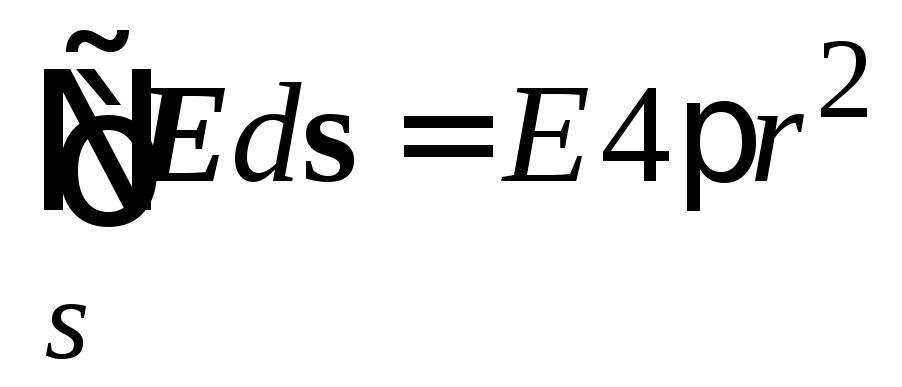

.

Aizstājot izteiksmi, lai aprēķinātu spriegumu, mēs saņemam

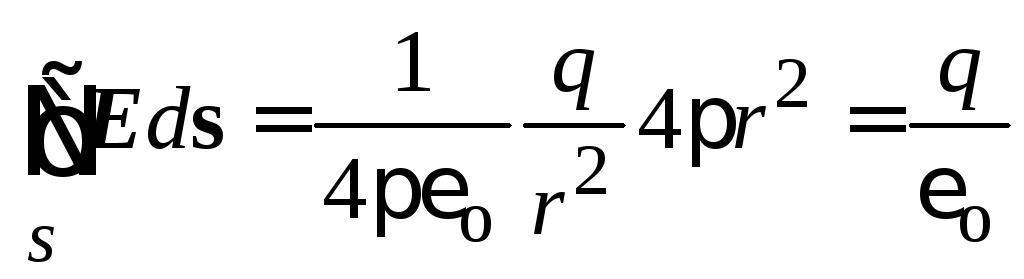Var parādīt šo lauka stiprības vektoru punkts caur slēgtu virsmu būs vienāds 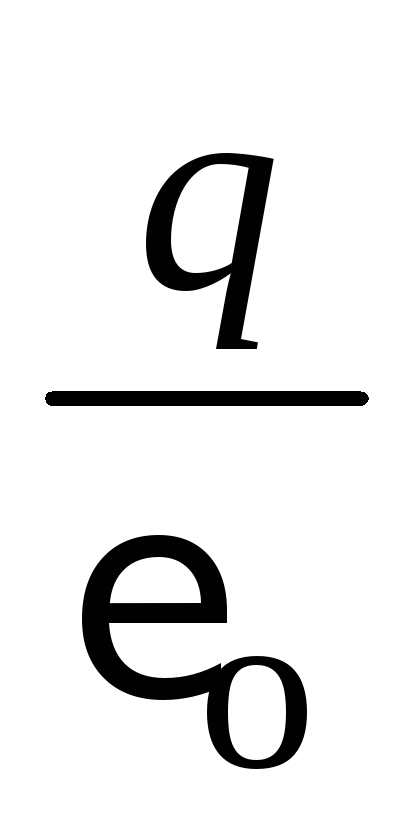un gadījumā, kad maksa nav sfēriskās virsmas centrā.

Turklāt plūsma būs vienāda pat tad, ja virsmai būs kāda forma.

Ja virsma aptver vairākus maksājumus q. i. , katra maksas plūsma caur slēgto virsmu būs vienāda ar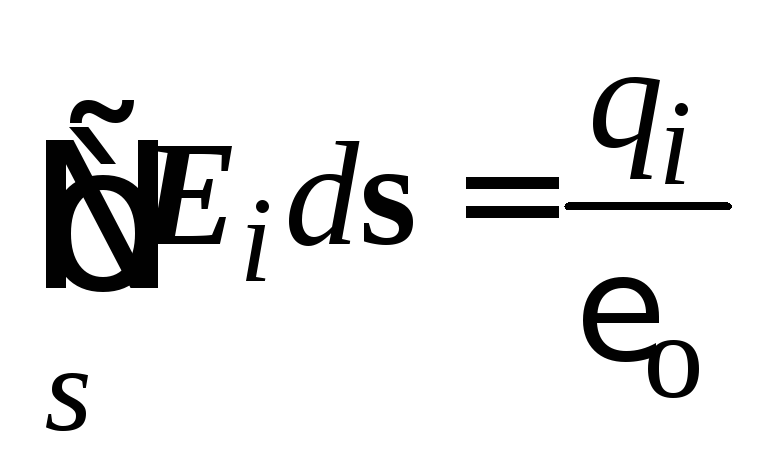

. Visu maksājumu radītā kopējā plūsma būs vienāda

.

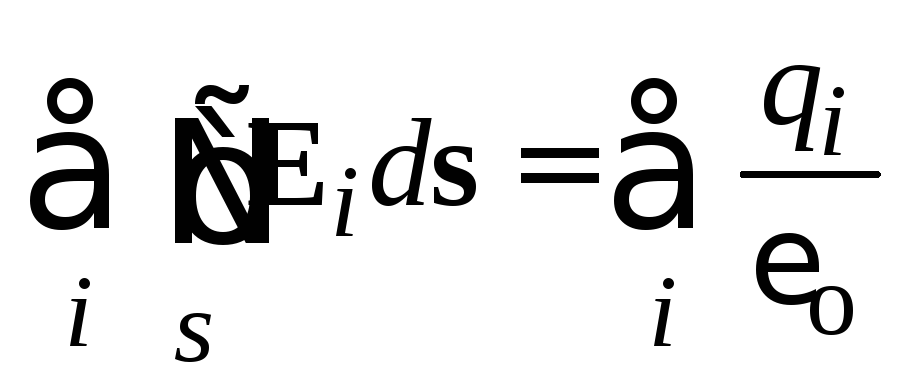Summācijas un integrācijas secības mainīšana un ņemot vērā, ka saskaņā ar superpozīcijas principu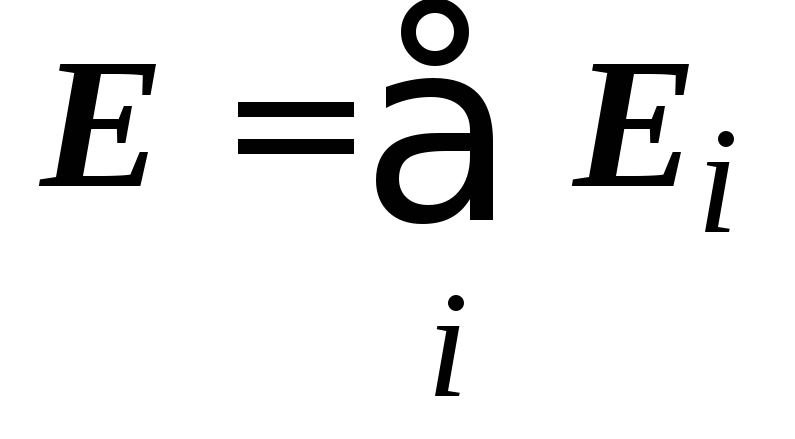

Saņemt

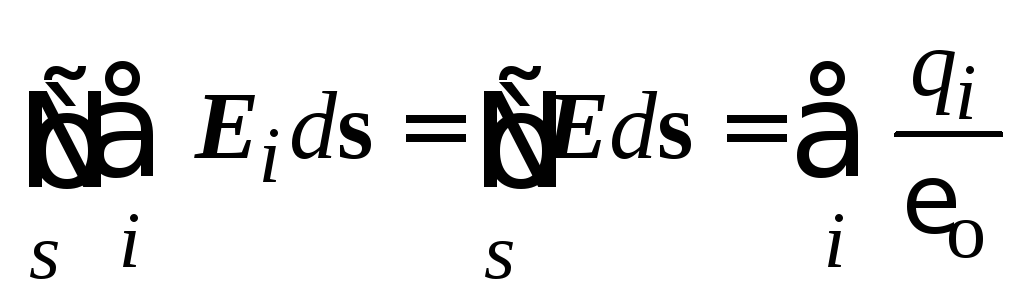kur E. - vektora sprieguma vektors, ko rada visas maksas, uz kurām attiecas slēgta virsma.

Tātad analīze ļāva šādu attiecību:

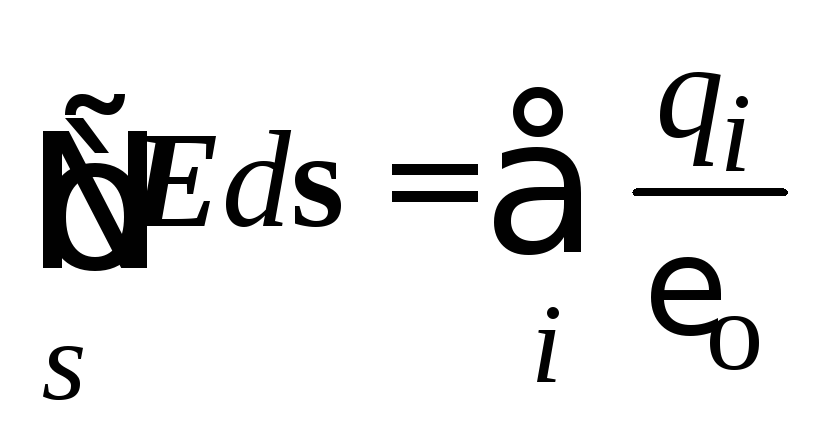Šai attiecībai ir daudzpusīgs raksturs, un to sauc par Gauss Theorem: plūsma sprieguma elektriskā lauka caur slēgtu virsmu ir vienāda ar attiecību maksu, kas pārklāta ar šo virsmu uz elektrisko konstantu.

Lūdzu, ņemiet vērā: Gausa teorijas izteiksmē nav nekādu maksu pozīcijas īpašības q. i. .

Tas nozīmē, ka spēka vektora plūsma nav atkarīga no tā, kā maksu ir iekļautas slēgtā virsmā. Turklāt sprieguma vektora stiprums nemainīsies, ja mainīsies virsmas segumu savstarpēja izkārtojums.

Gausa teorēmas praktiskā vērtība ir tā, ka tas ir ievērojami vienkāršots, aprēķinot laukus, kas izveidoti ar simetriskiem maksas sadalījumiem. Tādā gadījumā jūs varat izvēlēties virsmu tādā formā, ka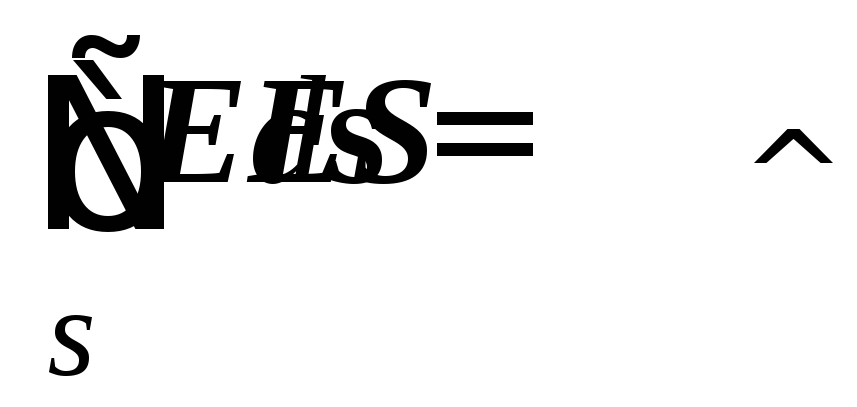

kur S.  - platība slēgtās virsmas, kas caurdurtā elektriskā laukā.

E r \u003d f s \u003d 4 2 \u003d 2 b m.

2. piemērs: vietne S \u003d 3m2 atrodas vienotā laukā 100 N / cl. Cik līnijas šķērso šo platformu, ja leņķis ir 30º (2.4. Att.).

E ┴ \u003d E SIN 300 \u003d 50 N / CL

F \u003d e ┴ · S \u003d 50 · 3 \u003d 150 līnijas

2.2. Plūsma vektora plūsma.

Tātad, uz piemēriem, mēs parādījām, ka, ja elektroenerģijas līnijas ir viendabīgas

elektriskais lauks spriedze e caurspiest dažus rotaļu laukumus, tad spriedzes plūsma (mēs izmantojām, lai izsauktu numuru silest līnijas caur rotaļlaukumu) tiks noteikts ar formulu

Fr e \u003d es \u003d ESCO α \u003d en s,

kur e n ir vektora produkts uz normālu uz šo vietni (2.5. Att.).

Un vērtību F e šeit un to sauc par plūsmu vektora elektrisko lauka stiprības caur vietni, ti. Definīcija:

Kopējais strāvas līniju skaits, kas iet caur virsmu, tiek saukts par sprieguma vektora plūsmu caur šo virsmu.

Vector formā varat ierakstīt

	F e \u003d (e, s) ir divu vektoru skalāra produkts, \\ t

kur vektors s \u003d n s.
Tiem. Plūsma vektors
		E ir skalārs, kas atkarībā no leņķa lieluma α

var būt gan pozitīvs, gan negatīvs . Apsvērt (2.6, 2.7. Att.).

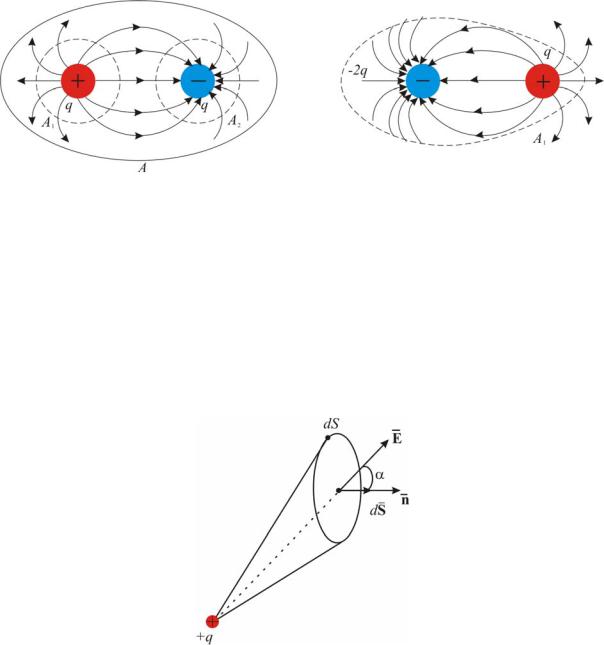
Šai konfigurācijai plūsma caur virsmu A, negatīvs (aprēķiniet elektropārvades līniju skaitu).

Fig. 2.6. 2.7

2.6. Attēlā - virsma ir 1 ieskauj pozitīva maksa Un plūsma šeit ir vērsta uz āru, I.E.F E\u003e 0. Virsma 2 - ieskauj negatīva maksa Un šeit, E.< 0 направлен внутрь.

2.7. Attēlam - plūsma nebūs nulle, ja kopējā uzlāde virsmas iekšpusē nav nulle. Tiem. Plūsma ir atkarīga no maksas. Šajā ziņā teorēma Gauss.

2.3. Ostrogradsky-Gauss teorēma.

Tātad, atcerieties elektriskā lauka stiprības plūsmas plūsmu - ir vienāds ar sprieguma līniju skaitu, kas iet caur zonu S (2.8. Att.).


dife \u003d edscos α \u003d en ds

R2)

q 4 πR 2 \u003d q

4 πε 0 R 2 2 2 ε 0

Tiem. homogēnā laukā f E \u003d es ar patvaļīgs elektriskais lauks

Fe \u003d ∫ EN DS \u003d ∫ E DS

d s r \u003d ds n r - vektoru formā
DS orientācija telpā ir iestatīta, izmantojot vienu vektoru R. Tiem.
- virziens sakrīt ar ārējo normālu virsmas virzienu.
Aprēķiniet vektora e plūsmu caur	slēgta virsma	S, apkārtnē

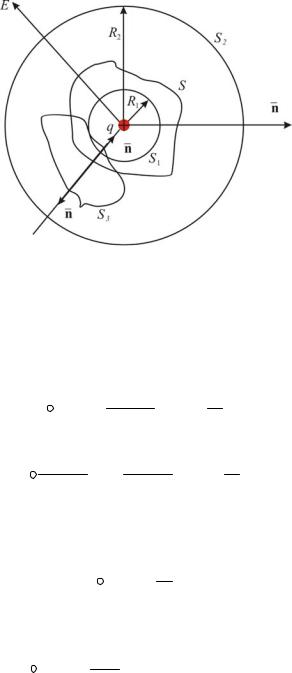
pavārs lādiņš Q (2.9. Att.).

Apļa centrs sakrīt ar maksas centru. Sfēras 1 rādiuss ir 1. Iebildums

katrs virsmas 1 punkts Ārējā normālā virzienā ir tāds pats un vienāds ar

E n \u003d.
E n \u003d.	4 πε.
	4 πε.
Tad plūst caur s 1
Tad plūst caur s 1
Fe \u003d ∫ EN DS \u003d		2 4 πR 1 2 \u003d
	4 πε0 R1

Aprēķiniet plūsmu caur S 2 (rādiuss

Fe \u003d ∫ 4 πε Q R 2 DS \u003d

S 2 R 0 2

Stiprības līnijas e sākas un beidzas bezgalības) no līnijas nepārtrauktības izriet, ka pavediena sprieguma virsmas būs vienāda ar tādu pašu lielumu:

Fe \u003d ∫ EN DS \u003d

Rezultāts ir derīgs ne tikai par vienu maksu, bet arī par jebkuru patvaļīgi izvietotu lādiņu virsmas iekšpusē.

Fe \u003d ∫ EN DS \u003d	Σq.	- teorēma Gaussa

Elektriskā lauka stiprības plūsma caur slēgtu virsmu vakuo ir vienāda ar algebrisko summu visām maksājumiem, kas atrodas iekšpusē, dalot ar ε0.

Aprēķinot plūsmu caur slēgtu virsmu, normālu n

pozitīva plūsma ir izveidota ar ierobežotu virsmu, līnijas ir iekļautas apjomā - negatīvā plūsma.

Ja starp mūsu sfērām ir vēl viena S 3 virsma, nevis

palīdzības maksa, tad, kā redzams no (2.9 att.). Katra rinda e līnija šķērsos šo virsmu divreiz: vienu reizi no pozitīvas puses - ieiet

virsmā 3, vēl viens laiks - no negatīvas puses - nāks no virsmām 3.

Iebildums rezultāts algebriskā sprieguma līniju iet cauri

slēgtā virsma S3 būs nulle, t.s. Kopējā plūsma, kas iet cauri 3, ir nulle.

Tādējādi, lai punktu uzlādētu Q, pilna plūsma caur jebkuru slēgtu virsmu S būs vienāds ar:

Fe \u003d 0 - ja maksa atrodas ārpus slēgtās virsmas un šo rezultātu

tas nav atkarīgs no virsmas formas un plūsmas zīme sakrīt ar uzlādes zīmi.

Kopumā elektriskie maksājumi Var būt "smeared" ar kādu masu blīvumu ρ atšķiras dažādās telpās. Atgādiniet citu koncepciju - maksas tilpuma blīvums

ρ =

kur DV ir bezgalīgi neliels apjoms.

Saskaņā ar fiziski bezgalīgi nelielu daudzumu DV, tas ir nepieciešams, lai saprastu šo tilpumu, kas, no vienas puses, ir pietiekami mazs, tāpēc, ka tās blīvuma nodevas tiek uzskatīta par to pašu, un no otras puses - tas ir pietiekami liels, lai Nevar izpausties bez maksas. Fakts, ka jebkura maksa ir katatēta veselā skaitā elementārās maksas vai Orp + (protonu). Pēc tam kopējā maksa

Σ qi \u003d ∫ ρdv

Tad no Gauss Theorem (2.3.7.) Mēs rakstām


	ε 0V ∫

Tas ir vēl viens no Gausa teorēmas forma, ja maksa ir nepārtraukta.

Ir nepieciešams pievērst uzmanību uz šādu apstākli: kamēr R

iE lauks ir atkarīgs no visu maksu konfigurācijas, Flux E caur patvaļīgu slēgto virsmu nosaka tikai algebriskā maksājuma summa virsmu iekšpusē. Tas nozīmē, ka, ja jūs pārvietot maksājumus, TE mainīsies visā, un uz virsmām, bet vektora plūsma caur šo virsmu paliks tāda pati. Amazing tipisks īpašums spriedzes.

2.4. Diferenciālā forma Gausa teorēmu.

Iebildums tas izveido saziņu starp tilpuma maksas blīvumsρ un maiņa tuvumā šīs telpas punktā

Pilna teksta meklēšana:

Mājas\u003e Abstrakts\u003e Fizika

Ievads ................................................. .................... ..... 3

Elektriskā lauka stiprums. Gausa teorēma integrētā formā ............................................ ................ 4

Elektromagnētiskā lauka teorijas parādīšanās un attīstība ......... .. 8

Secinājums ................................................. ....................... piecpadsmit

Saraksts atsaucēm izmanto ....................................... sešpadsmit

Ieviešana

Saskaņā ar modernām idejām elektriskās maksas nedarbojas tieši. Katra iekasētā iestāde izveido elektrisko lauku apkārtējā telpā, kurai ir jaudas darbība uz citām uzlādētām iestādēm.

Galvenais īpašums elektriskā lauka ir ietekme uz elektriskajām maksām ar kādu spēku. Tādējādi iekasēto struktūru mijiedarbība nav tieši tieši to ietekmi uz otru, bet izmantojot elektriskās jomas, kas saistītas ar iekasētajām iestādēm.

Lai kvantitatīvi noteiktu elektrisko lauku, tiek ieviesta jauda - elektriskā lauka stiprums.

Elektriskā lauka spriedzi sauc par fizisku vērtību, kas vienāda ar spēka attiecību, ar kuru laukums darbojas ar pozitīvu testa maksu, kas atrodas šajā telpā, uz šīs maksas lielumu:

Elektriskā lauka izturība - fiziskā vērtība. Vector E virziens sakrīt uz katru kosmosa punktu ar spēka virzienu, kas darbojas ar pozitīvu izmēģinājuma maksu.

Elektriskā lauka spriedze, ko rada maksas sistēma šajā telpā, ir vienāda ar vektoru summu elektrisko lauku elektrisko lauku, kas izveidots tajā pašā punktā ar maksu atsevišķi:

Šis elektriskā lauka īpašums nozīmē, ka lauks ir pakļauts superpozīcijas principam.

Elektriskā lauka stiprums. Gauss teorēma integrālā formā

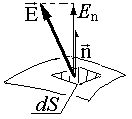
Ļaujiet n būt vienam normālam DS platformai (pietiekami mazs, lai novārtā izmēģināt elektrisko spriegumu e teritorijā). DF E-Electrical Stream Stream caur šo platformu ir definēts kā parastā komponenta E un DS produkts:

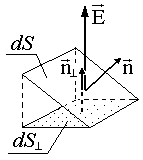
DF E plūsmas zīme acīmredzami ir atkarīga no savstarpējās orientācijas normālas un spriedzes. Ja šie divi vektori veido asu leņķi, plūsma ir pozitīva, ja stulba ir negatīva.

Plūsma DF E caur spilventiņu, kas slīpi uz elektroenerģijas līniju (tas ir, vektors e) ir vienāds ar plūsmu caur šai vietnes projekciju plaknē, kas ir perpendikulāra barošanas līnijai (sk. 1.1.2. Att.):

Šī vienlīdzība (1.1.1) izriet no definīcijas (1.1.1) DF E un teorēmas leņķiem ar savstarpēji perpendikulāriem pusēm.

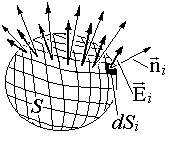
Plūsma F E Elektriskā spriegums E caur slēgtu virsmu S (1.3.3. Attēls) ir definēts kā elementāro plūsmu summa, izmantojot visas virsmas platformas. Limitā, kad vietņu skaits N tendence uz bezgalību, plūsmu daudzums caur platformām iet uz virsmas neatņemamu no normālas E N intensitātes sastāvdaļas:

K. Gauss 1844. gadā apliecina teorēma (Gausa teorēma neatņemamā veidā), kas nosaka savienojumu lauka avotiem un spriedzes plūsmas caur patvaļīgu virsmu apkārtējiem avotiem.

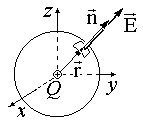
Par pierādījumu, izņemiet palīglīdzekļu formulu. Plūsma no punkta maksas, patvaļīga apkārtējā darbības jomā.

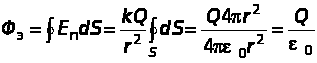. (1.1.4)

Punkta uzlādes līnijas perpendikulāri koncentriskā sfēras virsmai (sk. 1.1.4. Attēlu). Ņemot vērā šo faktu, formula (1.1.4) ir iegūta no loma lauka izteiksmes. Kā redzams, šajā gadījumā plūsma f e nav atkarīga no sfēras rādiusa un ir atkarīgs tikai no Q.

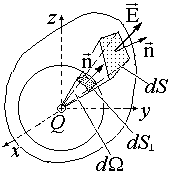
No (1.1.2) un (1.1.4) No tā izriet, ka plūsma uzlādes lauka caur jebkuru virsmu, kas saistītas ar lādiņu, plūst caur sfēru patvaļīgu rādiusu, koncentriska maksa. Patiešām, punkta uzlādes lauka plūsma, izmantojot jebkuru platformu DS, cirsts ar korporālu leņķi d no patvaļīgas virsmas, ir tāda pati kā plūsma caur sfēras platību cirsts ar to pašu ķermeņa stūra. Lauks Stream f e caur sfēru, kā jau minēts, nav atkarīgs no tā rādiusa. Tāpēc punkta uzlādes lauka stiprības plūsma caur virsmas s (sk. 1.3.5. Att.), Norāda formulā (1.3.4). No formulas (1.3.4) un superpozīcijas princips seko Gausa teorēmam neatņemamajā formā: pilna elektriskā lauka stipruma plūsma, izmantojot patvaļīgu slēgto virsmu, kas ir kā izplatīts (tilpums, virsma utt.) Uzlādējiet Q, ko aprēķina pēc formulas

Kad Gausa teorēma tiek piemērots, lai atrisinātu problēmas, ir jāatceras, ka vienādojumā (1.1.5) Q - visu maksājumu summa garīgās virsmas iekšpusē, caur kuru tiek aprēķināta plūsma, ieskaitot maksājumus, kas pieder pie atomiem un molekulām vidēja (tā sauktās saistītās maksas).

Lauka stiprums E caur jebkuru aizvērtu virsmu, kurā pilna maksa ir nulle, ir arī nulle.

Elektromagnētiskā lauka teorijas parādīšanās un attīstība

Gadsimtā 17-18 gadu laikā elektromagnētiskie procesi arvien vairāk iekļuva zinātnē: fizika un ķīmija. Pasaules elektromagnētiskā attēla laikmets, kas mainīja mehānisko vienu.

Maxwell nepārprotami redzēja elektromagnētisko likumu pamatprincipu, kas veica lielo optikas un elektroenerģijas sintēzi. Tas bija tas, kas izdevās samazināt optiku uz elektromagnētismu, radot elektromagnētisko gaismas teoriju un smējās jaunos veidos ne tikai teorētiskajā fizikā, bet arī tehnikā, sagatavojot augsni radio inženierijai.

Faradayays parādījās jaunā veidā, lai pētītu elektroenerģijas un magnētiskās parādības, norādot uz vides lomu un ieviešot jēdzienu, kas aprakstīta tā, izmantojot elektropārvades līnijas. Maxwell deva idejām par matemātisko konversiju, ieviesa precīzu terminu "elektromagnētiskais lauks", kas vēl nebija Faraday, formulēja matemātiskos likumus šajā jomā. Galilee un Newton nodeva pasaules mehāniskās priekšstatu, Faraday un Maxwell ir pasaules elektromagnētiskā attēla pamati.

Maxvela elektromagnētiskā teorija izstrādā darbos "uz spēka fiziskajām līnijām" (1861-1862) un "dinamiskā lauka teorija" (1864-1865). Viņš rakstīja šos darbus vairs Aberdeen, bet Londonā, kur viņš saņēma profesoru King - koledžā. Šeit Maxwell tikās ar Faradeju, kurš bija vecs un slims. Maxwell, saņemot datus, kas apliecina elektromagnētisko raksturu pasaulē, nosūtīja tos Faraday. Maxwell rakstīja: "Tās pasaules elektromagnētiskā teorija (Faraday)" domās par radiālām vibrācijām "(Phil. Mag., 1846. gada maijs) vai" eksperimentālie pētījumi "(Exp. Rec, 447 lpp.) - Tas būtībā ir būtībā Tas pats, ko es sāku attīstīties šajā rakstā ("dinamiskā lauka teorija" -phil. Mag., 1865), izņemot to, ka 1846. gadā nebija datu, lai aprēķinātu sadales ātrumu. J.K.M. ".

1873. gadā Maxvela galvenais darbs tika atbrīvots "Trase no elektrības un magnētisma". Viņš sāka uzrakstīt populāru paziņojumu par savu teoriju "Elektroenerģija elementārā prezentācijā", bet tam nebija laika, lai to pabeigtu.

Maxwell bija daudzpusīgs zinātnieks: teorētiķis, eksperimentētājs, tehniķis. Bet fizikas vēsturē viņa vārds galvenokārt ir saistīts ar tās elektromagnētiskā lauka teoriju, ko sauc arī par Maxwell teoriju vai Maxwell elektrodinamiku. Tā ieradās zinātnes vēsturē kopā ar tādām būtiskām vispārinājumiem kā Ņūtona mehānika, relativistisko mehānika, kvantu mehānika, un iezīmēja jaunā fizikas posma sākumu. Saskaņā ar Likumu par zinātnes attīstību, ko formulējis Aristotelis, viņa izvirzīja zināšanas par dabu uz jauno, augstākais līmenis un tajā pašā laikā bija vairāk nesaprotama, abstrakts nekā iepriekšējās teorijas, "mazāk skaidri par mums", saskaņā ar uz Aristoteli.

Maxwell sāka attīstīt savu teoriju 1854.gadā

Maxwell raksturo elektrotorisko stāvokli ar trim funkcijām, kas izsauc elektrotoniskās funkcijas vai elektrotonikas stāvokļa sastāvdaļas. Mūsdienu apzīmējumos šī vektora funkcija atbilst potenciālajam vektoram. Šā vektora līkumainā integrālā sastāvdaļa pa slēgtu līniju Maxwell zvaniem "pilnu elektrotonisko intensitāti pa slēgtu līkni." Par šo vērtību, tā atrod pirmo efektu elektrotonisko stāvokli: "pilnīga elektrotonisko intensitāte gar robežu virsmas elementa kalpo kā mēru summas magnētiskās indukcijas iet caur šo elementu, vai, citiem vārdiem sakot, pasākums Magnētisko elektropārvades līniju skaits, kas ieņem šo elementu. " Mūsdienu apzīmējumos šo likumu var izteikt ar formulu:

ja A ir potenciālā vektora komponents DL līknes elementa virzienā, BN ~ parastā indukcijas vektora sastāvdaļa normāla virzienā uz DS virsmas elementu.

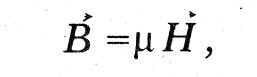
saistoša magnētiskā indukcija ar sprieguma vektoru magnētiskais lauks N.

Trešais likums sasaista magnētiskā lauka H ar spēku tās pašreizējā pašreizējā I. Maxvela formulē to kā tas: "Pilnīga magnētiskā intensitāte pa līniju, kas ierobežo daļu no virsmas, kalpo kā elektriskās strāvas plūsmas daudzuma mērs caur šo virsmu. " Mūsdienu apzīmējumos šo priekšlikumu apraksta ar formulu

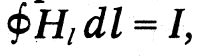
ko tagad sauc par pirmo Maxwell vienādojumu integrālajā formā. Tas atspoguļo eksperimentālo faktu, āra erstended: strāvu ieskauj magnētiskais lauks.

Ceturtais likums ir OHM likums:

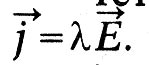
Lai raksturotu jaudas mijiedarbību Maxwell strāvas ievieš vērtību, ko tos sauc par magnētiskais potenciāls. Šī vērtība ir pakļauta piektajam likumam: "Pilnīgu elektromagnētisko potenciālu slēgtā strāva tiek mērīta ar pašreizējo elektrotisko intensitāti gar ķēdi, kas tiek uzskatīts virzienā pašreizējā:

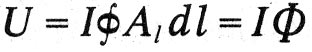
Maxvelas sestais likums attiecas uz elektromagnētisko indukciju: "Elektromotikas spēku, kas darbojas diriģenta elementā, tiek mērīts ar elektrotoniskās intensitātes atvasinājumu, neatkarīgi no tā, vai šis atvasinājums ir atkarīgs no elektrotoniskās stāvokļa vērtības vai virziena izmaiņām." Jo mūsdienu apzīmējumu, šis likums ir izteikts ar formulu:

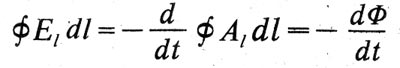
Tas ir otrais Maxwell vienādojums neatņemamā formā. Ņemiet vērā, ka Maxvela elektromotīvju spēks sauc par elektrisko lauka stiprības vektora cirkulāciju. Maxwell apkopo Faraday - Lenchana indukcijas likumu, ņemot vērā, ka magnētiskās plūsmas (elektrotoniskās valsts) laika izmaiņas rada virpotisko elektrisko lauku, kas pastāv neatkarīgi no tā, vai ir slēgtas vadības ierīces, kurās šis lauks ir aktuāls vai nē. Visizplatina Ersteda Maxwell likumu vēl nedod.

Vēl viena svarīga ziņa ir ieviest jēdzienus kompensēt un kompensēt strāvas. Pārvietošanās, saskaņā ar Maxwell, ir raksturīga dielektriskās valstis elektriskajā jomā. Pilna plūsma pārvietošanas caur slēgtu virsmu ir vienāda ar algebrisko summu apsūdzības iekšpusē virsmas. Tas ievieš fundamentālo jēdzienu kompensēt strāvu. Šī strāva, kā arī vadītspēja strāva rada magnētisko lauku. Tāpēc Maxwell apkopo vienādojumu, ko pašlaik sauc par pirmo Maxvela vienādojumu, un ievieš maiņas strāvu pirmajā daļā. Mūsdienu apzīmējumos šis Maxvell vienādojums ir veidlapa:

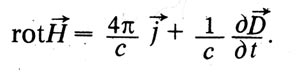
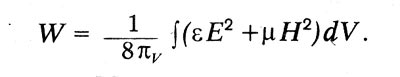
Visbeidzot, Maxwell konstatē, ka tās elastīgajā vidē šķērsvirziena viļņi ir izplatīti ar gaismas ātrumu. Šis būtiskais rezultāts noved pie tā svarīga secinājuma: "šķērsvirziena svārstību svārstību ātrums mūsu hipotētiskajā vidē, kas aprēķināts no Kolrauha un Weber elektromagnētisko eksperimentu, tāpēc tieši sakrīt ar gaismas ātrumu, kas aprēķināts no Fizo optisko eksperimentu, kas aprēķināts Mēs diez vai var atteikties no izstāšanās, ka gaisma sastāv no tā paša mediju šķērsvirziena svārstībām, kas izraisa elektriskās un magnētiskās parādības. Tādējādi XIX gadsimta 60. gadu sākumā. Maxwell jau ir atradis pamatus tās teorijas elektroenerģijas un magnētisma un sniedza svarīgu secinājumu, ka gaisma ir elektromagnētiskā parādība.

Maxvela teorijā par "elektromagnētiskā brīža" lielums ir saistīts ar magnētisko plūsmu. Vector potenciāla cirkulācija slēgtā kontūrā ir vienāda ar magnētisko plūsmu caur kontūras virsmu. Magnētiskajai plūsmai ir inerciālas īpašības, un indukcijas elektromotikas spēks atbilstoši Lenz regulai ir proporcionāla magnētiskā plūsmas maiņas ātrumam ar pretējo zīmi. Līdz ar to indukcijas elektriskā lauka spriedze:

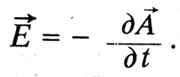
Maxwell uzskata, ka šī izteiksme ir līdzīga izpausme inerces jaudai mehānikā:

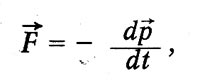
Mehānisks impulss vai kustības skaits. Šī analoģija izskaidro terminu, ko ieviesa Maxwell par vektora potenciālu. Paši vienādojumi elektromagnētiskais lauks Maxvela teorijā viņiem ir redzams, kas nav moderns.

Mūsdienu formā Maxvela vienādojumu sistēma ir šāda:

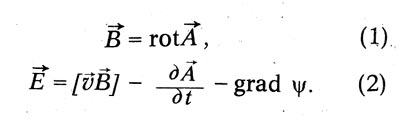
Attiecības starp pārvietojumu D un elektrisko lauku elektriskajā laukā E Maxwell ir izteikts vienādojumā:

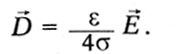
Tad izlaida vienādojumu Divd \u003d P un vienādojumu, kur

kā arī robežas stāvokli:

Tā ir Maxvela vienādojumu sistēma. Vissvarīgākais šo vienādojumu secinājums ir šķērsvirziena elektromagnētisko viļņu pastāvēšana magnetizētā dielektriskajā ātrumā: kur

Šis secinājums tika iegūts viņa pēdējā sadaļā "Dynamic Field teorija", ko sauc par "elektromagnētisko teoriju gaismas". "... Elektromagnētisma zinātne," Maxwell raksta šeit, - noved pie pilnīgi tādiem pašiem secinājumiem kā optikas attiecībā uz perturbāciju virzienu, kas var izplatīties pa laukumu; Abas šīs zinātnes apstiprina šo svārstību šķērsošanu, un abi sniedz tādu pašu sadales ātrumu. " Uz gaisa šī ātruma c - gaismas ātrums (Maxwell apzīmē to v), dielektriskajā tas ir mazāks, kur

Tādējādi refrakcijas indekss n, saskaņā ar Maxwell, nosaka elektriskās un magnētiskās īpašības vidē. Nav magnētiskā dielektriskā kur

Tas ir slavenais Maxwell attiecība.

V.Tomson 1853. gadā viņš izmeklēja konkrētā konteinera vadītāja izlādi, izmantojot šīs formas vadītāju un pretestību. Piemērojot enerģijas saglabāšanas likumu uz budžeta izpildes apstiprināšanas procesu, tā atvasināja izlādes procesa vienādojumu šādā formā: \\ t

kur Q ir elektroenerģijas daudzums izlādējamajā diriģents noteiktā brīdī t, jaudu vadītājs, K ir galvaniskā pretestība aizturēšanas, un "konstante, ko var saukt par elektrodinamisko jaudu izlādes" un kas Tagad mēs izsaucam pašindukcijas koeficientu vai induktivitāti. Thomson, analizējot šo vienādojumu risinājumu dažādās raksturīgās vienādojuma saknēm, konstatē, ka tad, kad vērtība

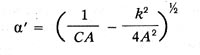
tai ir derīga vērtība (1 / ca\u003e 4 * (k / a) 2), tad risinājums rāda ", ka galvenais diriģents zaudē savu maksu, maksās mazāk nekā elektroenerģijas apgrieztās zīmes, atkal tiek izlādēta, atkal tas pagriezās Lai būtu jāmaksā vēl mazāks skaits sākotnējās zīmes elektroenerģijas, un šī parādība atkārto bezgalīgo skaitu, līdz līdzsvars ir izveidots. " Šo bojājumu svārstību cikliskā frekvence:

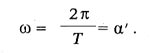
Tādējādi svārstību periods var iesniegt pēc formulas:

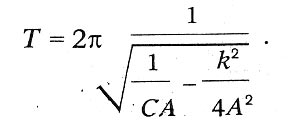
Ar nelielām pretestības vērtībām mēs iegūstam slaveno Thomson formulu:

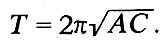
Secinājums

Electric Field ir īpašs lauks, kas pastāv ap ķermeņiem vai daļiņām ar elektrisko lādiņu, kā arī brīvā formā elektromagnētiskajos viļņos. Elektriskais lauks ir tieši neredzams, bet to var novērot savā darbībā un ar ierīcēm. Elektriskā lauka galvenā darbība ir iestāžu vai daļiņu paātrinājums ar elektrisko lādiņu.

Elektrisko lauku var uzskatīt par matemātisku modeli, kas apraksta elektriskā lauka lieluma vērtību šajā telpā. Douglas Jancoli rakstīja šādi: "Jāuzsver, ka lauks nav sava veida viela; tas ir pareizāks, tas ir ļoti noderīgs koncepcija ... jautājums par" realitāti "un elektriskā lauka esamību Faktiski ir filozofisks, diezgan pat metafizisks jautājums. Fizikā ideja par lauka izrādījās ļoti noderīga - tas ir viens no lielākajiem sasniegumiem cilvēka prātā. "

Elektriskais lauks ir viens no vienas elektromagnētiskā lauka sastāvdaļām un elektromagnētiskās mijiedarbības izpausme.

Izmantotās literatūras saraksts

Dmitrieva V.F., Prokofiev v. Lpp. Fizikas pamati. - M.: Augstskola, 2003

Kalashnikov N. P., Smondyrev M. A. Fizikas pamati. - M.: Drop, 2003

Makarov E. F, Ozers R. P. Fizika. - M.: Zinātniskā pasaule, 2002

Savelyev I.V. General Fizikas kurss: studijas. Rokasgrāmata: universitātēm. 5 kn. KN.2. Elektroenerģija un magnētisms - 4. ed., Pererab.- M.: Zinātne, Fizmatlit, 2003, SS. 9-30, 41-71

Trofimova t.i. Fizikas kurss: studijas. Rokasgrāmata: universitātēm. - 5th ed., Sure.- m.: Augstāks. Shk., 2003, SS. 148-164

Detlox A. A., Yavorsky B. M. Fizikas kurss: Pētījumi. universitāšu rokasgrāmata. - 2. Ed., Universitāte. un add-m.: augstāks. Shk., 20049, SS. 182-190, 193-202.

IRODOV I. E. Elektromagnētisms. Pamatlikumi. - 3rd Ed., Upar.-M.: Pamatzināšanu laboratorija, 2000, SS. 6-34.

Kursa \u003e\u003e Fizika

Lauki. Teorēma Gausa iebildums integrālis forma 4. Vector lauka atšķirības. Teorēma Gausa Diferenciālā forma Secinājumu saraksts ... LV:. (1.3.3.) K. Gauss 1844. gadā pierādīts teorēma (teorēma Gausa iebildums integrālis forma), izveidojot sakaru avotus ...

Elektrostatiskā lauka izpēte

Laboratorijas darbi \u003e\u003e Fizika

Potenciāls. Vēl viens būtisks attiecība ir teorēma Gausa (In integrālis forma), apgalvojot, ka vektora plūsma ... elektrostatiskais lauks. 11. Dodiet definīciju teorēmas Gausa iebildums integrālis forma. 12. Sniedziet iespējamo definīciju ...

Mehānika. Molekulārā fizika

Kopsavilkums \u003e\u003e Fizika

Ostrogradsky teorēma, jūs varat formulēt teorēmu Gausa B. integrālis forma: Vector Stream caur jebkuru ... nulle:. - teorēma Gausa. Izmantojot Ostrogradsky teorēmu, mēs saņemam teorēmu Gausa Vektoram diferenciālā forma