§ 15. Potential. Energy system of electrical charges. Work on the movement of charge in the field

Basic formulas

 Potential electric field There is a value equal to the ratio of the potential energy of a point positive charge, placed at a given point of the field, to this charge;

 \u003d n / Q.,

or the potential of the electric field is the value equal to the ratio of the operation of the field for the movement of a point positive charge from this field point to infinity to this charge:

=A./ Q..

The potential of the electric field in infinity is conditionally adopted equal to zero.

Note that when the charge in the electric field is moved A. v.S. external forces are equal to the module of work A. s.P. Field forces and opposite to her sign:

A. v.S. = – A. s.P. .

 Electric field potential created by a point charge Q.on distance r.from charge

 Potential of an electric field created by a metal carrier charge Q.sphere radius R., At the distance of the center of the center of the sphere:

within the sphere ( r.<R.)

;

on the surface of the sphere ( r.=R.)

;

beyond sphere (r.> R.)

.

In all the formulas for the potential of the charged sphere, the dielectric permeability of a homogeneous limitless dielectric surrounding the sphere.

 Potential of the electric field created by the system ppoint charges, at a given point in accordance with the principle of superposition of electric fields are equal to algebraicummepotentials 1 , 2 , ... , n. created by separate point charges Q. 1 ,Q. 2 , ...,Q. n. :

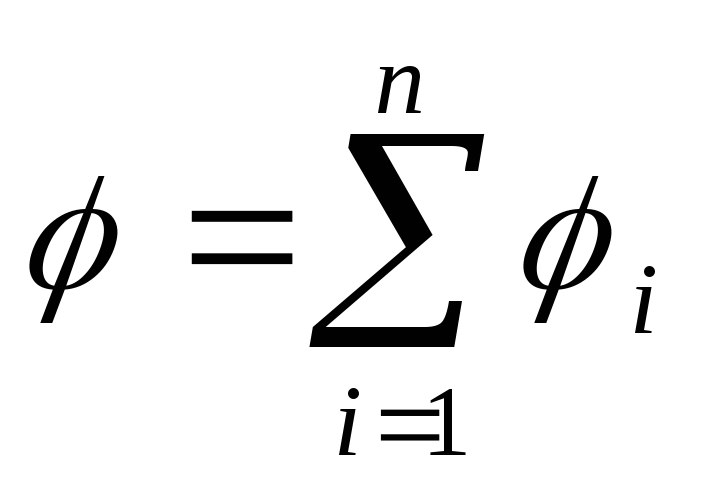
 Energy W.interaction system of point charges Q. 1 ,Q. 2 , ...,Q. n. Determined by the work that this system of charges can perform when removing relative to each other in infinity, and is expressed by the formula

,

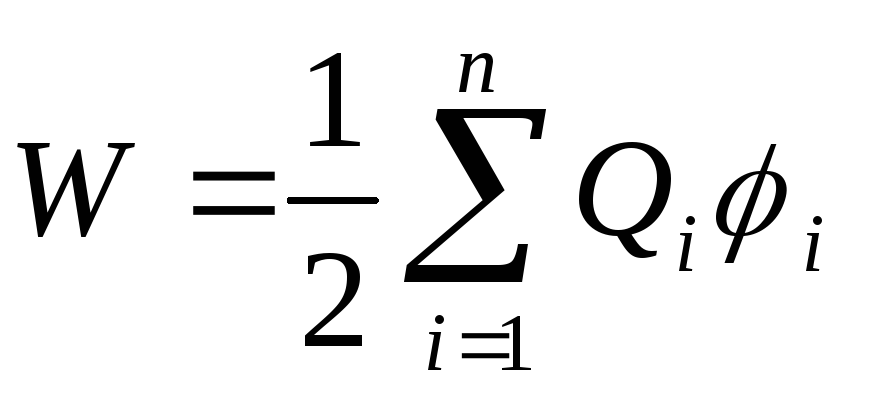where  i. - the potential of the field created by all p-1 charges (with the exception of the 1st) at the point where the charge is located Q. i. .

 Potential is associated with electric field strength by the ratio

E.\u003d -Grad.

In the case of an electric field with spherical symmetry, this connection is expressed by the formula

,

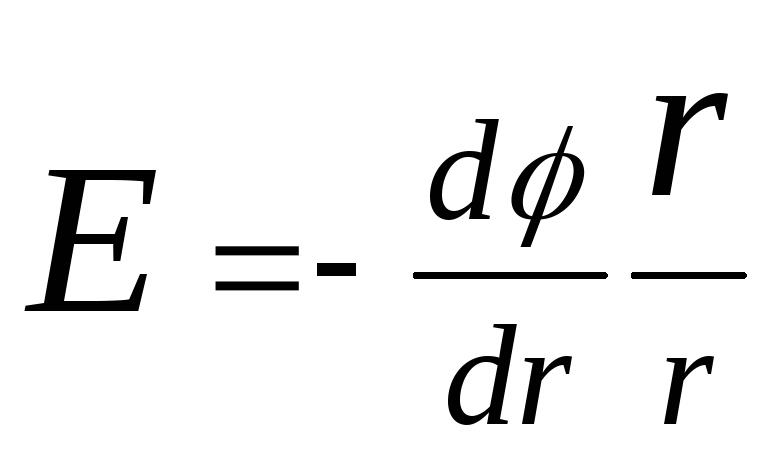or in scalar form

,

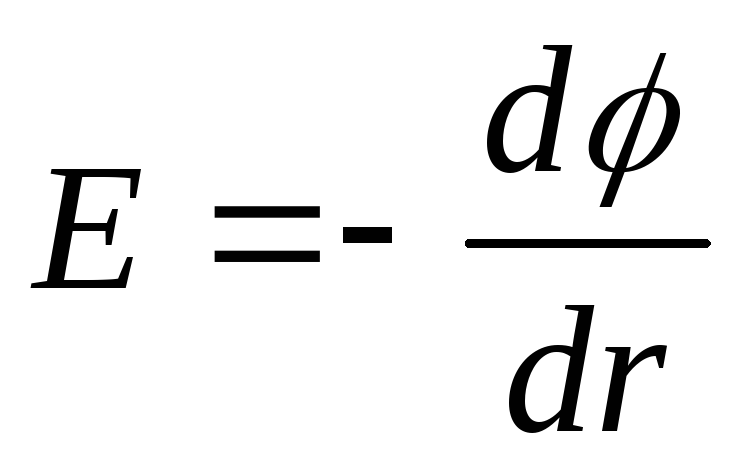and in the case uniform field, i.e. fields whose tension at each point is the same in both the module and in the direction,

E.=( 1 – 2 ,)/d.,

where  1 I. 2 - potentials of points of two equipotential surfaces; d. - distance between these surfaces along the electric force line.

 Work performed by electric field when moving point charge Q.from one point of the field having potential 1 to another having potential 2 ,

A.=Q.( 1 - 2 ), or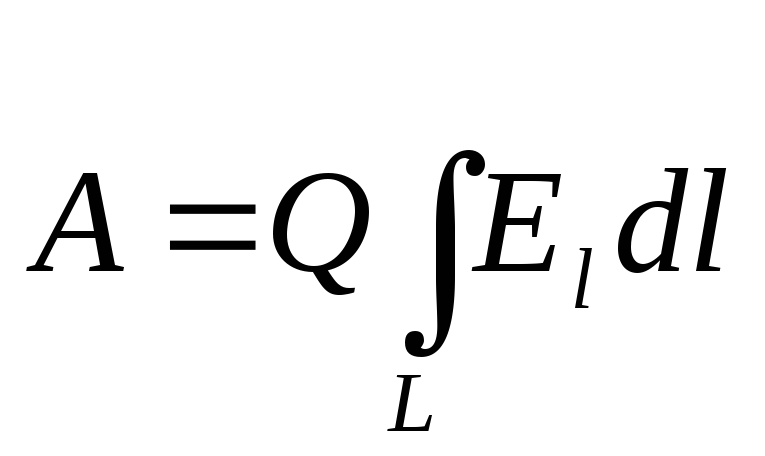

,

where E. l. - projection of tension vector E.on the direction of movement; dL - move.

In the case of a homogeneous field, the last formula takes

A.= Qelcos. ,

where l.- movement; - The angle between the directions of the vector E.and movement l..

Examples of solving problems

Example 1.Positive charges Q. 1 \u003d 3 μKl and Q. 2 \u003d 20 NDLs are in vacuo at a distance r. 1 \u003d L, 5 m from each other. Define work A.which must be done to bring the charges to the distance r. 2 \u003d 1 m.

Decision.We put that the first charge Q. 1 remains fixed, and the second Q. 2 Under the action of external forces moves to the field created by charge Q. 1 , approaching him from the distance r. 1 \u003d T, 5 m to r. 2 \u003d 1 M. .

Job BUT"external force to move charge Q.from the same field with potential 1 to another whose potential 2 is equal to the module and the opposite of the work sign BUTfield forces to move charge between the same points:

A "\u003d -A.

Job BUTfield forces to move charging A.=Q.( 1 - 2 ). Then work BUT"external forces can be recorded in the form

A." = –Q.( 1 - 2 )=Q.( 2 - 1 ). (1)

Potentials of points of principles and end of the way are expressed by formulas

;

.

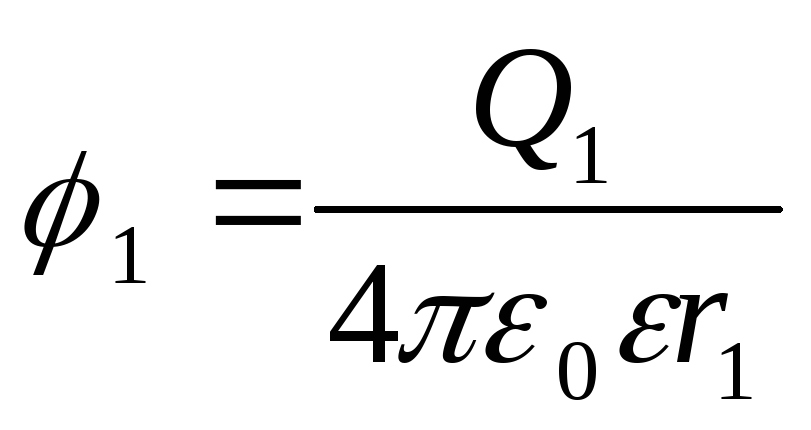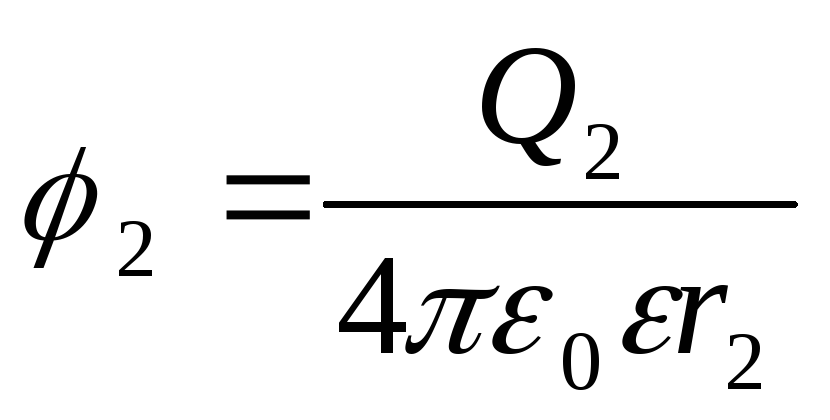Substituting the expressions  1 I. 2 In formula (1) and considering that for a given case, a transferred charge Q.=Q. 2 , get

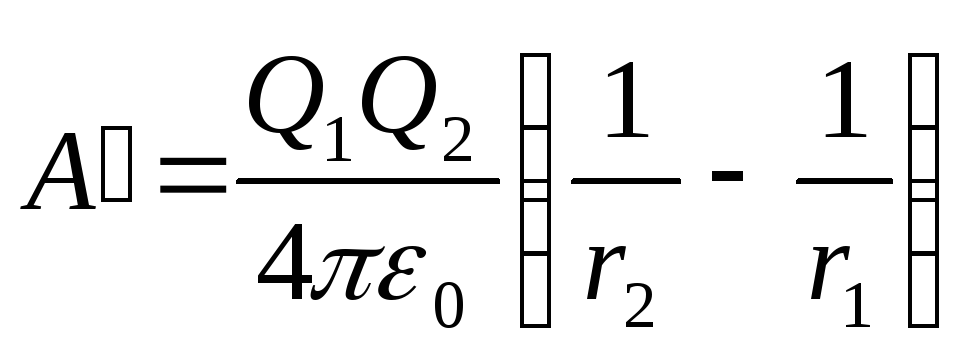. (2)

If we consider that 1 / (4 0 )=910 9 m / f, then after substitution of values \u200b\u200bof values \u200b\u200bin formula (2) and calculations will find

A."\u003d 180 μJ.

Example 2.Find a job BUTcharge Travel Fields Q.\u003d 10 nkl from the point 1 exactly 2 (Fig. 15.1), which are between two differently charged with surface density \u003d 0.4 μl / m 2 endless parallel planes, distance l.between which is 3 cm.

R

measure.There are two ways to solve the problem.

1st way.Workfield forces to move charge Q from point 1 potential fields 1 exactly 2 potential fields 2 Find by formula

A.=Q.( 1 - 2 ). (1)

To determine the potentials at points 1 and 2 we will conduct equipotential surfaces through these points. These surfaces will be planes, as the field between two uniformly charged endless parallel planes is homogeneously. For such a field, the ratio is true

 1 - 2 =El., (2)

where E -field strength; l. - the distance between the equipotential surfaces.

Field tension between parallel endless varianetically charged planes E.=/ 0 . Substituting this expression E.in formula (2) and then expression 1 - 2 in formula (1), we get

A.= Q.( /  0 ) l..

2nd way.Since the field is uniform, the force acting on the charge Q.When it is moved constant. Therefore, the work of the charge of the charge from the point 1 exactly 2 can be calculated by the formula

A.\u003d F.  r.cOS, (3)

where F. - force acting on charge;  r.- charging module Q.from the point 1 exactly 2; - The angle between the directions of movement and power . But F.= QE= Q.( /  0 ). Substituting this expression F.in equality (3), as well as noticing that r.cos \u003d. l., get

A.=Q.(/ 0 )l.. (4)

Thus, both solutions lead to the same result.

Substituting in the expression (4) the value of values Q., , 0 and l.We find

A.\u003d 13.6 μJ.

Example 3.On the thin thread, curved on the arc of the circumference with the radius R., uniformly distributed charge with linear density \u003d 10 nkl / m. Determine tension E.and the potential -electric field created by such p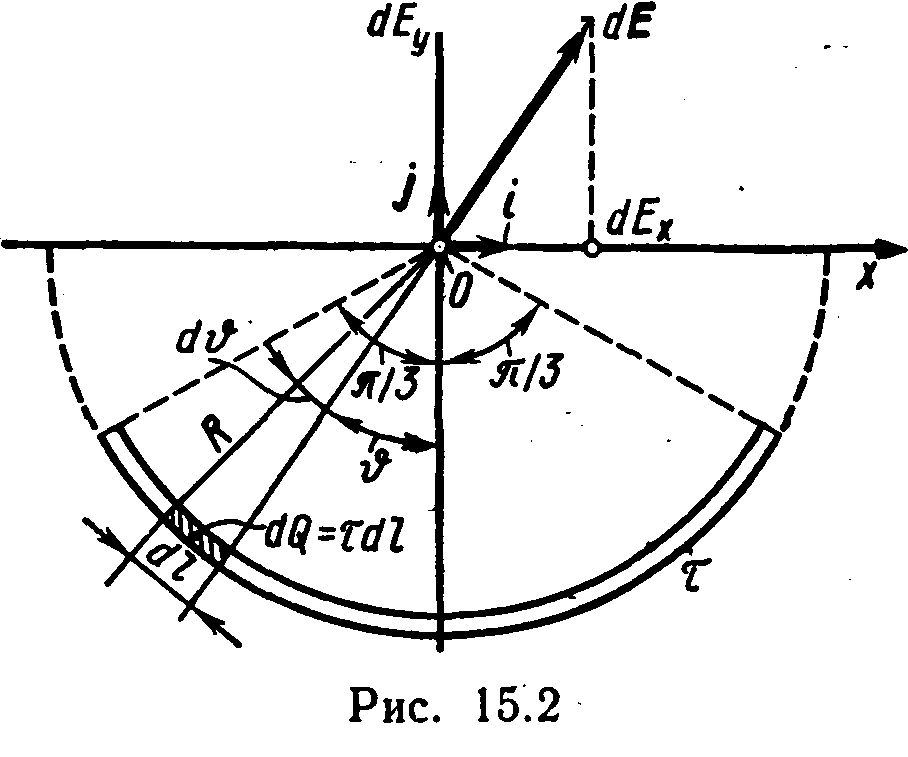

ascrowded charge at point ABOUTwhich coincides with the center of the curvature of the arc. Length l.the threads is 1/3 of the circumference length and is equal to 15 cm.

Decision.We choose the axis of the coordinates so that the origin of the coordinate coincides with the center of the curvature of the arc, and the axis w.it was symmetrically located relative to the ends of the arc (Fig. 15.2). On the threads allocate the length element l.. Charged Q.\u003d d. l., located on a dedicated area, can be read point.

Determine the electric field strength at the point ABOUT. To do this, find at first tensions E.charged Fields Q.:

,

where r.-Dius vector directed from elementd l.to the point, the tension in which is calculated. Express vector D. E.through projections dE. x. c.and dE. y. On the axis of coordinates:

,

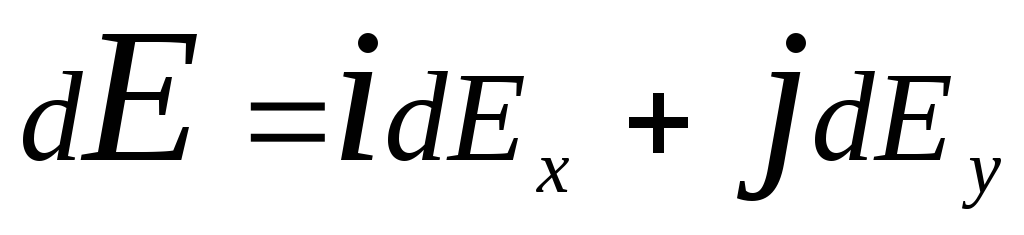where i.and j.- single vectors of directions (orts).

Tension E.find integration:

.

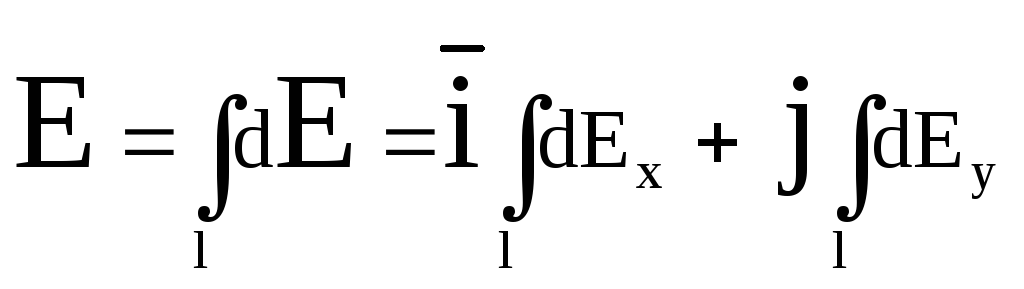Integration is conducted along the length arc l.. Due to symmetry integral 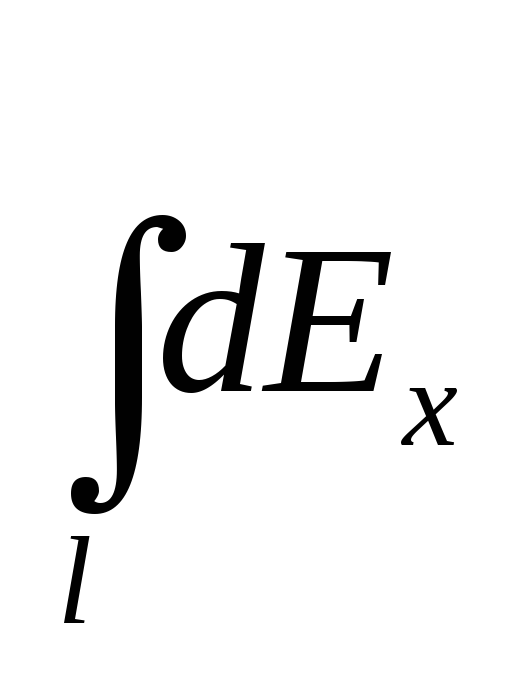equal to zero. Then

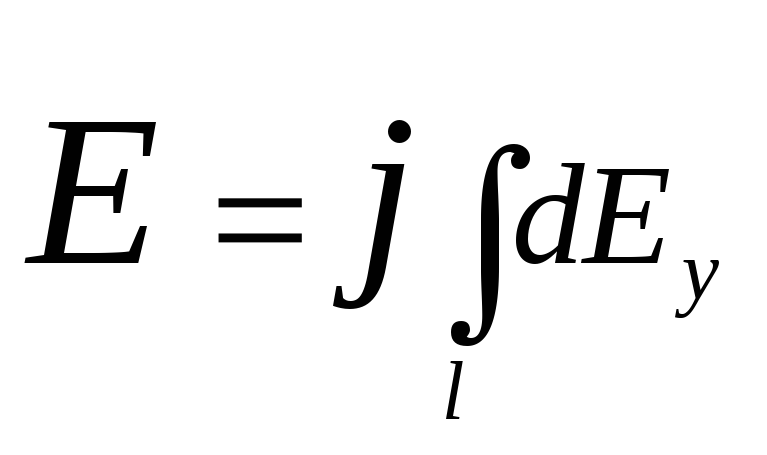, (1)

where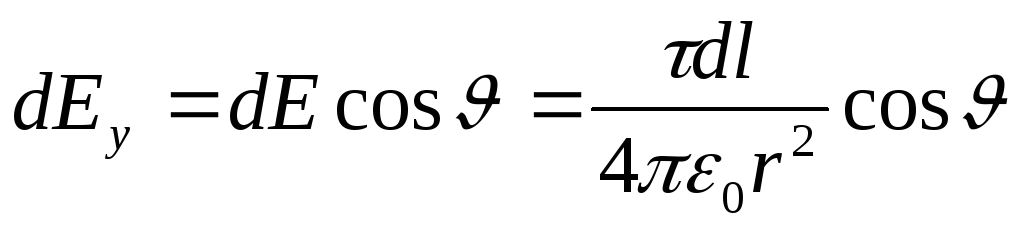

. Because r.=R.\u003d const l.=R.d. that

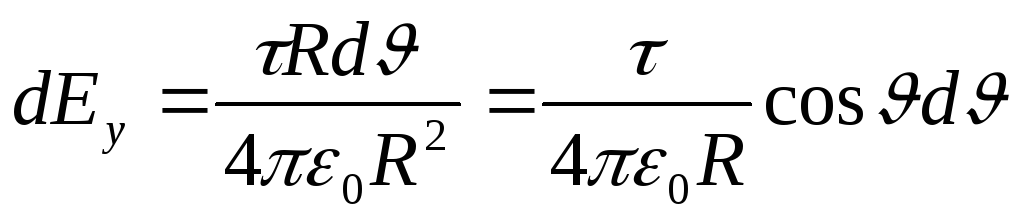
We substitute the expression found dE. y. in (1) and, taking into account the symmetric arc location relative to the axis OU,the integration limits take from 0 to / 3, and the result will double;

.

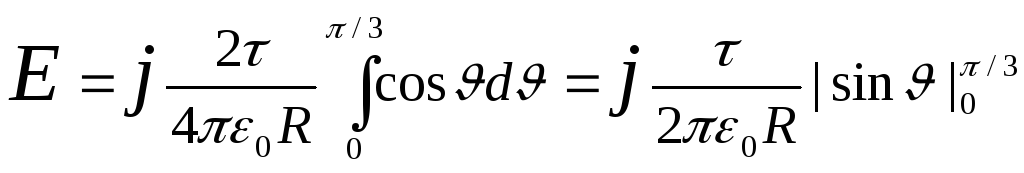Substituting the above limits and expressing R.through the length of the arc (3 l.= 2. r.), we get

.

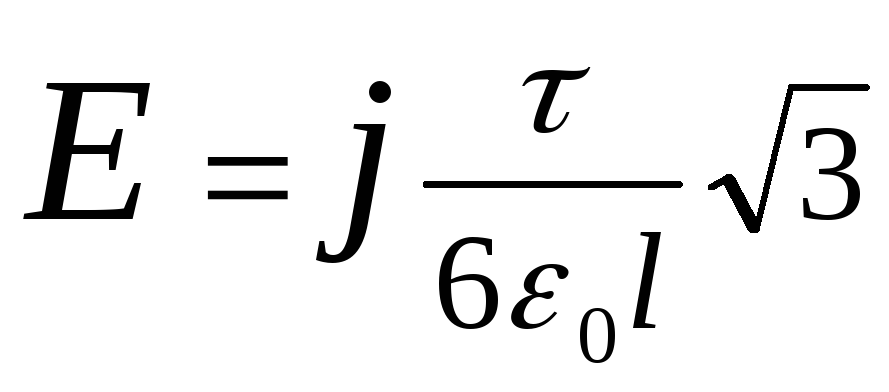From this formula you can see that vector E.coincides with the positive direction of the axis OUSubstituting importance l.in the last formula and making calculations, we will find

E.\u003d 2,18 kV / m.

We define the potential of the electric field at the point ABOUT. We will find at first the potential, created by a point charged Q.at point ABOUT:

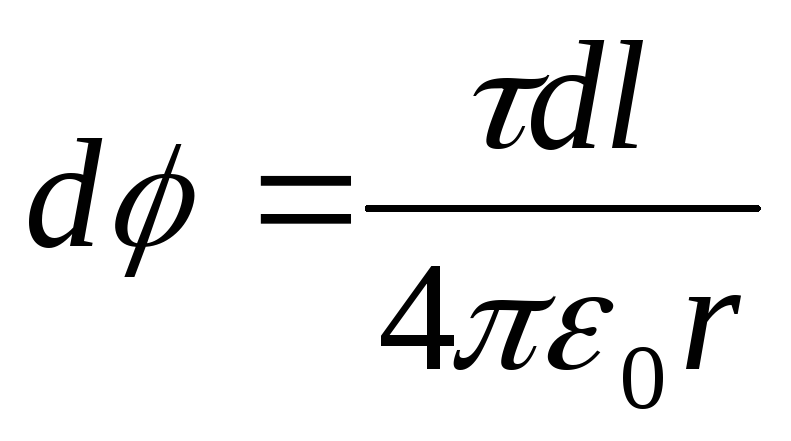
Replace r.on the R.and we will integrate:

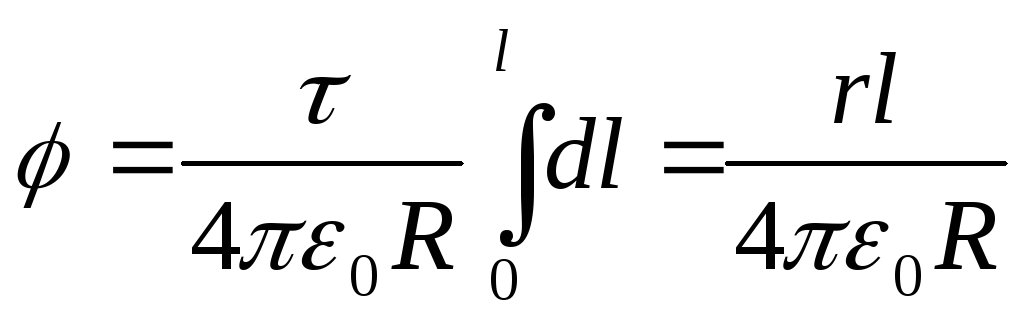.Because l.=2  R./3, that

 \u003d  / (6 0 ).

By making calculations for this formula, we get

Example4 . The electric field is created by a long cylinder with a radius R.= 1cm , uniformly charged with linear density \u003d 20 NL / M. Determine the difference in the potentials of two points of this field located at distances a. 1 \u003d 0.5 cm and but 2 \u003d 2 cm from the surface of the cylinder, in its middle part.

Decision.To determine the difference in potentials, we use the relationship between the field strength and the change in the potential E.\u003d -Grad. For a field with axial symmetry, what is the field of the cylinder, this ratio can be written as

E \u003d - (d / D. r.) , ord \u003d - E.d. r..

Integrating the last expression, we will find the difference in the potentials of two points, which are disposed on r. 1 and r. 2 from the axis of the cylinder;

. (1)

Since the cylinder is long and points are taken close to its middle part, then to express the field strength, you can use the formula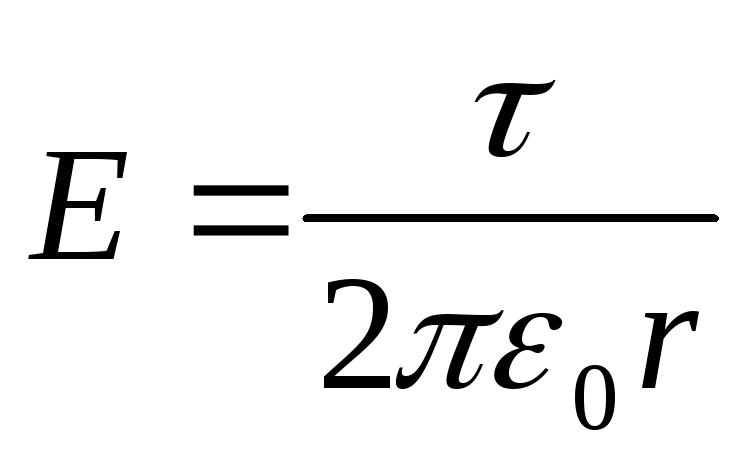

. Substituting this expression E.in equality (1), we get

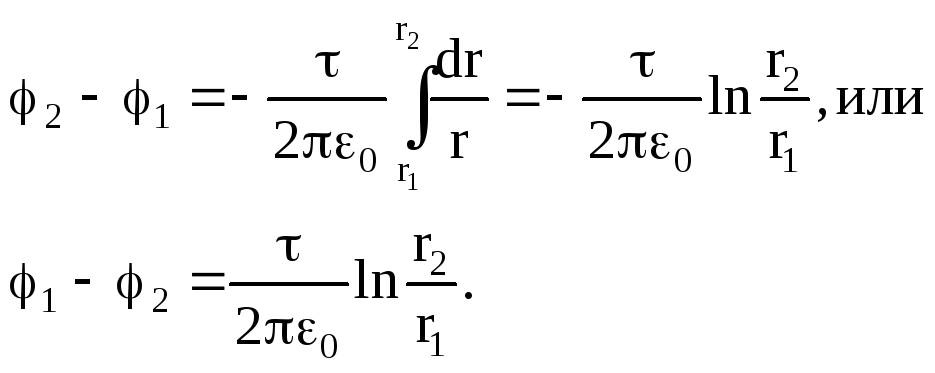(2)

Since values r. 2 and r. 1 Participated in a formula in the form of a relationship, they can be expressed in any, but only the same units:

r. 1 \u003d R + A 1 = 1.5 cm; r. 2 =R.+a. 2 \u003d 3cm .

Substituting the values \u200b\u200bof magnitude ,  0 ,r. 1 and r. 2 in formula (2) and computing, we will find

 1 - 2 \u003d 250 V.

Example 5.The electric field was created by a thin rod carrying uniformly distributed in length charge \u003d 0.1 μl / m. Determine the potential at the point removed from the end of the rod to the distance equal to the length of the rod.

Decision.The charge located on the rod cannot be considered point, so directly apply to the calculation of the potential of the formula

, (1)

fair only for point charges, it is impossible. But if you split the rod on the elementary segments D l., charged. l., located on each of them, can be viewed as a point and then formula (1) will be valid. Applying this formula, we get

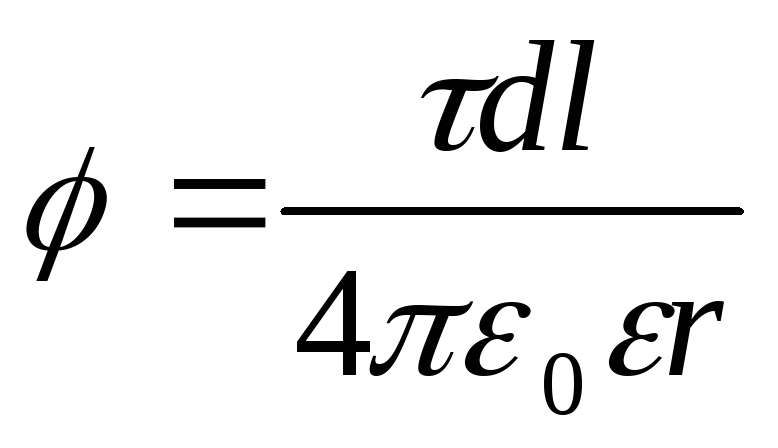, (2)

where r. - the distance of the point in which the potential is determined to the element of the rod.

From fig. 15.3 It follows that D l.=(r.d / COS). Substituting this expression D l.in formula (2), we will find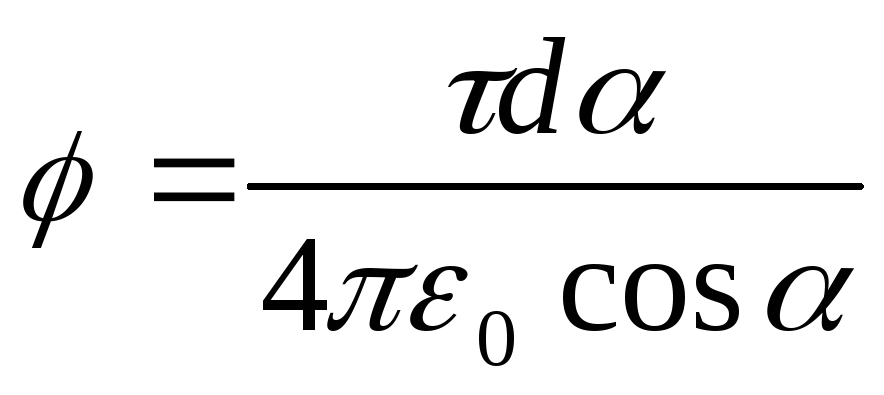

.

Integrating the resulting expression ranging from  1 Yes 2 , I get the potential created by all charge distributed on the rod: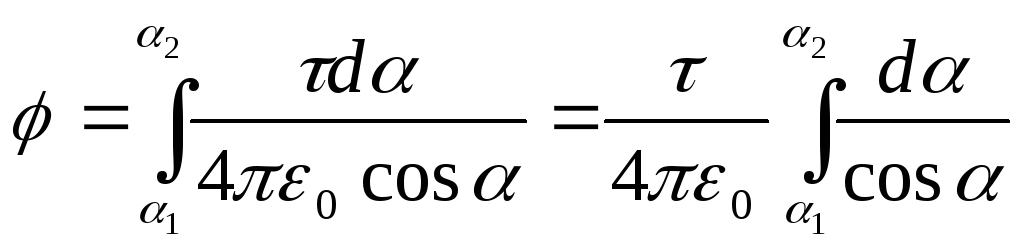

.

AT 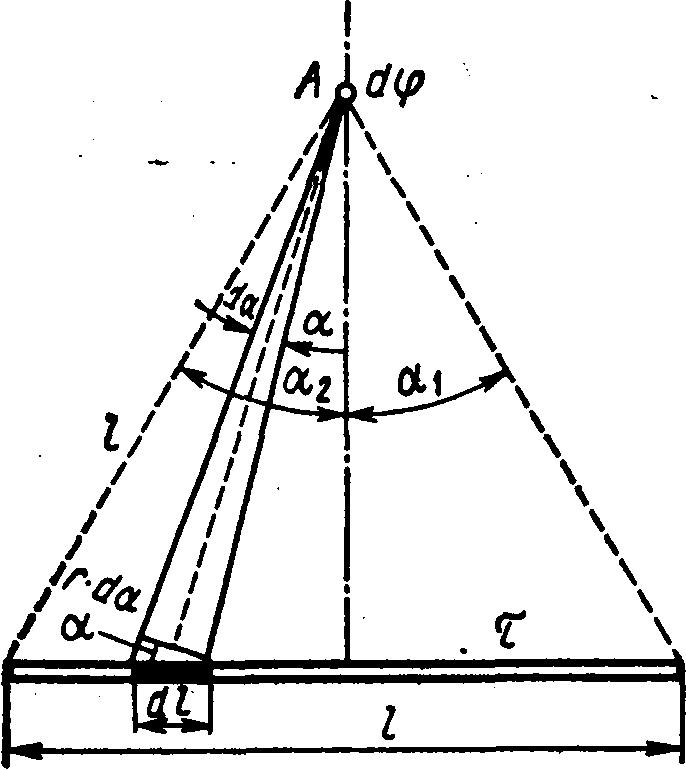point of Point Location Symmetry BUTrelative to the ends of the rod have 2 = 1 and therefore

.

Hence,

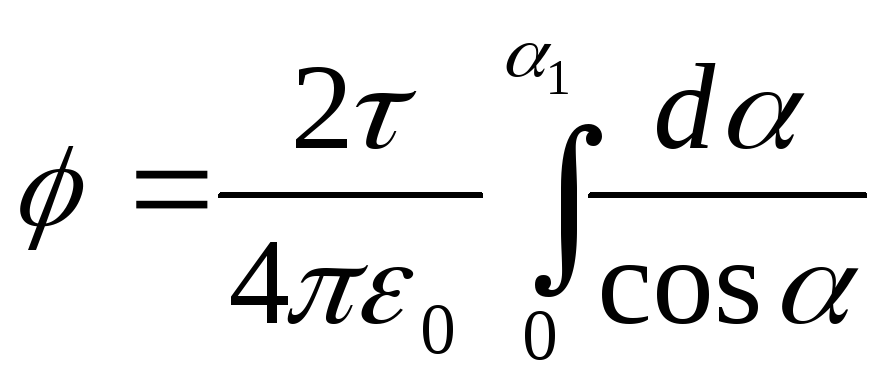.Because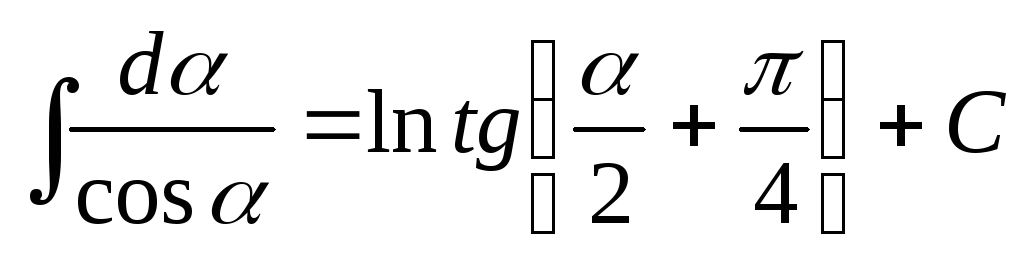

(see Table 2), then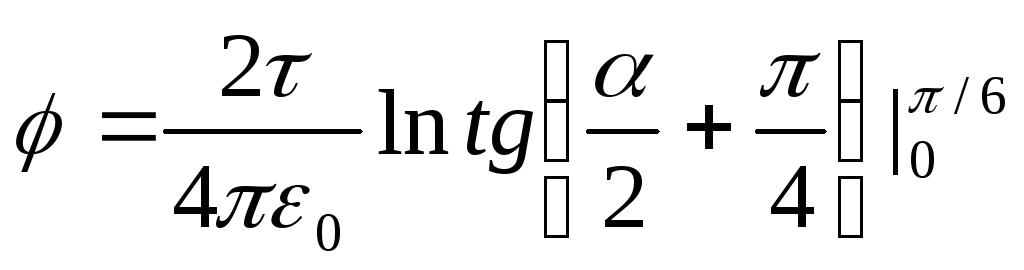

.

Substituting the integration limits, we get

By making calculations for this formula, we will find

Example 6.Electron at speedsV \u003d 1.8310 6 m / s flew into a homogeneous electric field in the direction opposite to the field strength vector. What the difference potentials U.must pass an electron to possess energy E. i. \u003d 13.6 EV *? (Possessing such an energy, an electron in a collision with a hydrogen atom can ionize it. The energy of 13.6 eV is called hydrogen ionization energy.)

Decision.The electron must pass such a difference in potentials. U,to the energy acquired at the same time W.in sum with kinetic energy T.which had an electron before entering the field, amounted to energy equal to the energy of ionization E. i. , i.e. W.+ T.= E. i. . Expressing in this formula W.= eUand T.=(m.v. 2 / 2), we get eU+(m.v. 2 /2)=E. i. . From here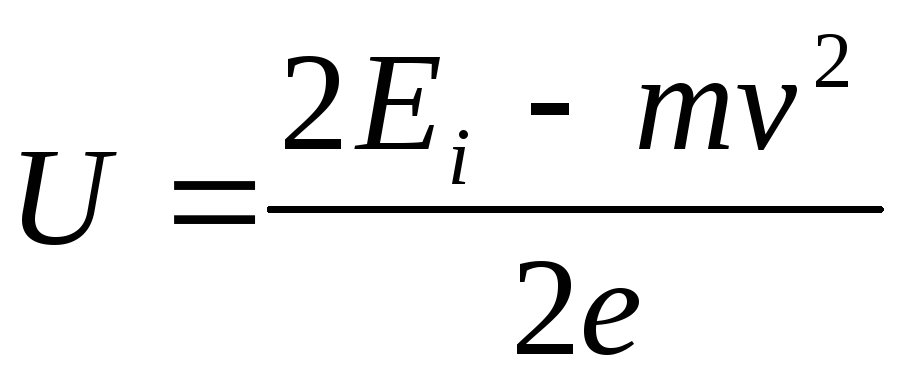

.

___________________

* The electron-volt (eV) is the energy that the particle acquires, having a charge equal to the charge of an electron, which has passed the difference in the potentials of 1 V. This generated unit of energy is currently allowed to be applied in physics.

Producing calculations in units of C:

U \u003d 4,15AT.

Example 7.Determine the initial speed υ 0 rapprochement of protons located at a fairly long distance from each other, if the minimum distance r. Min, which they can get close to 10 -11 cm.

R E W E N E. Between the two protons there are repulsive strengths, as a result of which the proton movement will be slowed. Therefore, the problem can be solved both in an inertial coordinate system (associated with the center of mass of two protons) and in non-inertocal (associated with one of the accelerated moving protons). In the second case, Newton's laws do not have place. The use of the principle of Dalambert is difficult due to the fact that the acceleration of the system will be variable. Therefore, it is convenient to consider the task in the inertial reference system.

Position the origin of the coordinates to the center of the masses of two protons. Since we are dealing with the same particles, the center of the masses will be at a point dividing in half the segment connecting particles. Regarding the center of mass, the particle will have at any point of time the same speed module. When the particles are at a fairly large distance from each other, speed υ 1 each particle is equal to half υ 0 , i.e. υ 1 =υ 0 /2.

To solve the problem, we use the law of energy conservation, according to which complete mechanical energy E.isolated system constant, i.e.

E \u003d T +P ,

where T.- the sum of the kinetic energies of both protons relative to the center of the masses; P is the potential energy of the charge system.

Express the potential energy to the initial P 1 and the final p 2 moments of movement.

In the initial moment, according to the condition of the problem, the protons were at a high distance, so potential energy can be neglected (p 1 \u003d 0). Consequently, for the initial moment, the total energy will be equal to kinetic energy T. 1 protons, i.e.

E \u003d T. L. . (1)

At the end moment, when the protons will bring together as much as possible, the speed and kinetic energy are zero, and the total energy will be equal to the potential energy of P 2, i.e.

E \u003d.P 2. . (2)

Equating the right parts of equalities (1) and (2), we get

T 1 \u003d p 2. (3)

Kinetic energy is equal to the sum of the kinetic energies of protons:

(4)

Potential energy of two charges Q. 1 I. Q. 2 in vacuo, is determined by the formula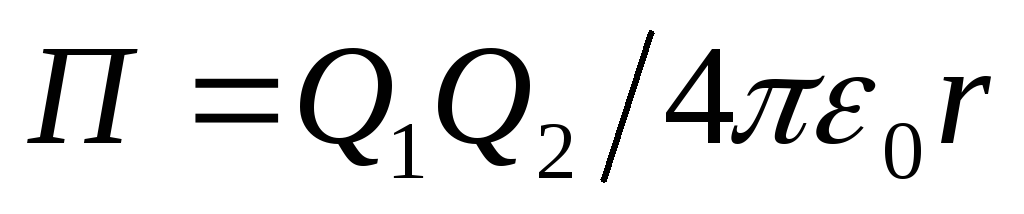

where r.- Distance between charges. Taking advantage of this formula, we get

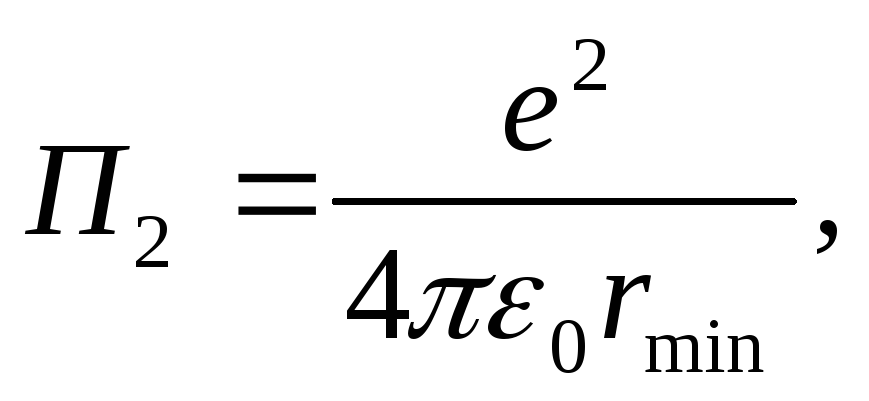(5)

Taking into account the equalities (4) and (5) of formula (3) will take

from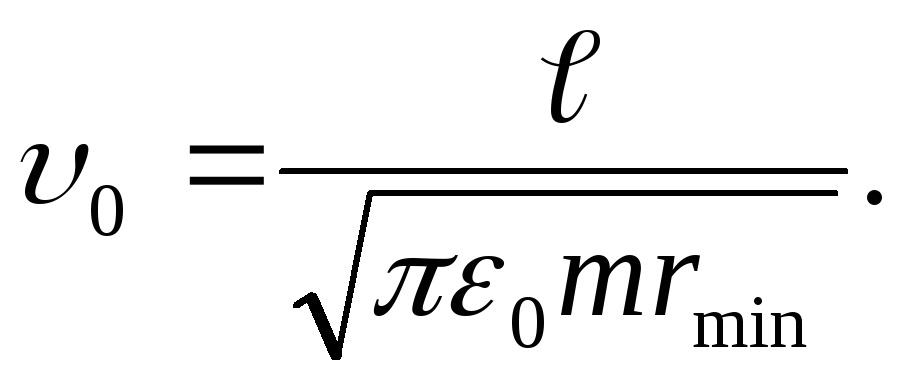

By calculating the resulting formula, we will find υ 0 =2,35 Mm / s.

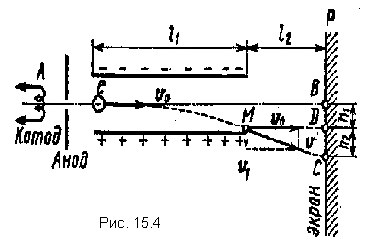Example 8.Electron without initial speed passed the difference in potentials U. 0 =10 kV and flew into space between plates of a flat capacitor charged to potential difference U. L \u003d 100 V, line ABparallel to the plates (Fig. 15.4). Distance d.between the plates is 2 cm. Length l. 1 condenser plates in the direction of electron flight is 20cm. Determine the distance Sunon the screen R,disposition of condenser on l. 2 \u003d 1 m.

R E W E N E. The movement of the electron inside the condenser consists of two movements: 1) by inertia along the line AUwith constant speed υ 0 , acquired by the difference of potentials U. 0 , which the electron passed to the capacitor; 2) evenly accelerated movement in the vertical direction to a positively charged plate under the action of constant power of the condenser field. Upon leaving the condenser, the electron will move evenly at speed υ, which he had at the point M.at the time of departure from the condenser.

From fig. 15.4 It can be seen that the desired distance | BC | \u003d H 1 + H. 2 , where S. h. 1 - the distance to which the electron is shown in the vertical direction while driving in the condenser; h. 2 - the distance between the d point on the screen in which the electron would hit, moving on the output of the capacitor in the direction of initial speed υ 0, and the point C, into which the electron will actually fall.

Express separately h. 1 I. h. 2 . Taking advantage of the length of the length of the path of uniformly accelerated movement, we will find

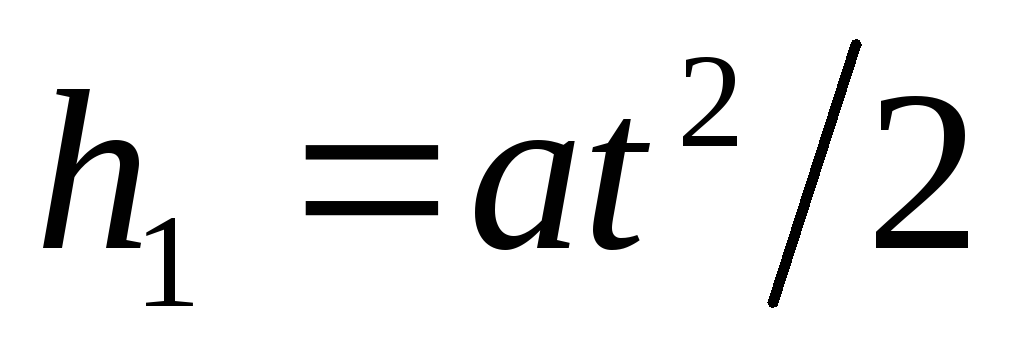. (1)

where but- acceleration obtained by an electron under the action of a capacitor field; t-electron flight time inside the condenser.

According to Newton's second law a \u003d f / m,where F.- the force with which the field acts on the electron; t-his mass. In its turn, F. \u003d EE \u003d EU 1 / D,where e.- electron charge; U. 1 - the difference of potentials between the plates of the capacitor; d.- Distance between them. Electron flight time inside the condenser Find from the formula of a uniform movement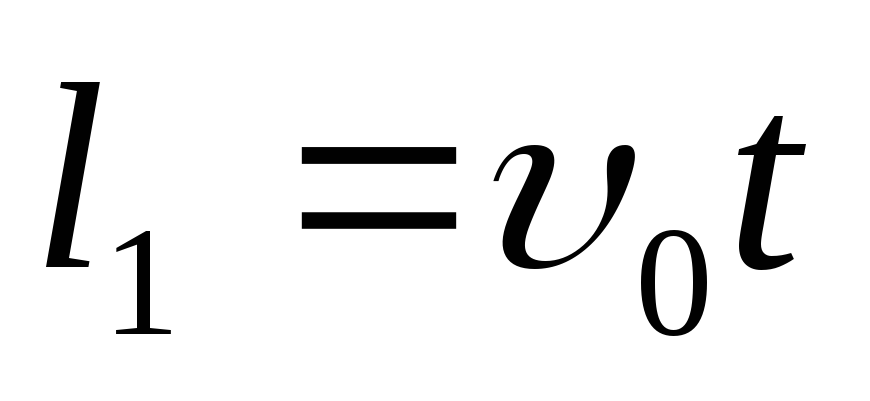

, from

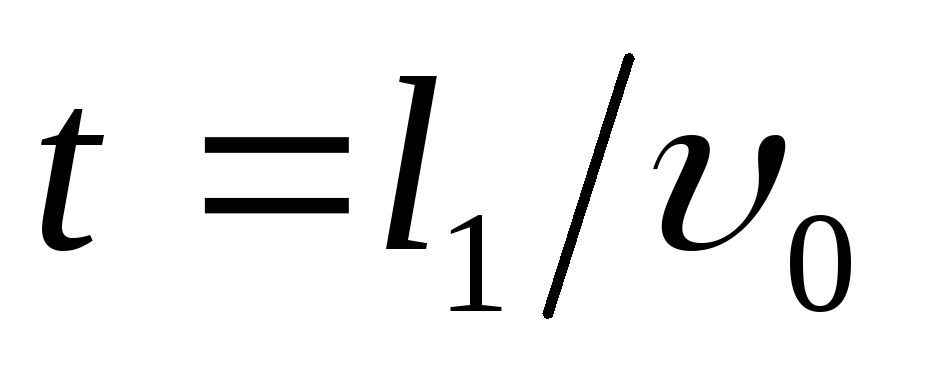
where l. 1 - Condenser length towing an electron flight. The expression of the speed will be found from the condition of equality of work performed by the field when moving the electron, and the kinetic energy acquired by them: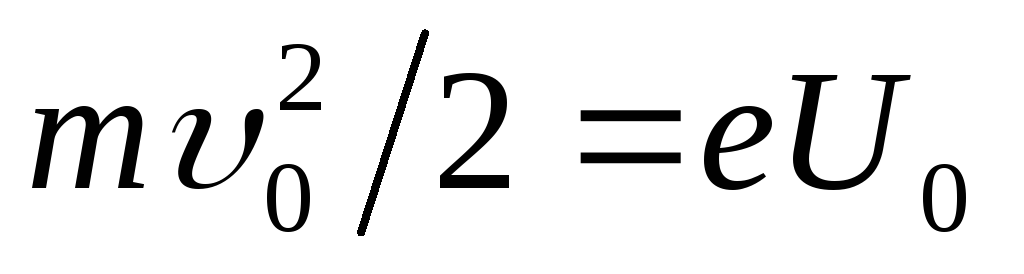

. From here

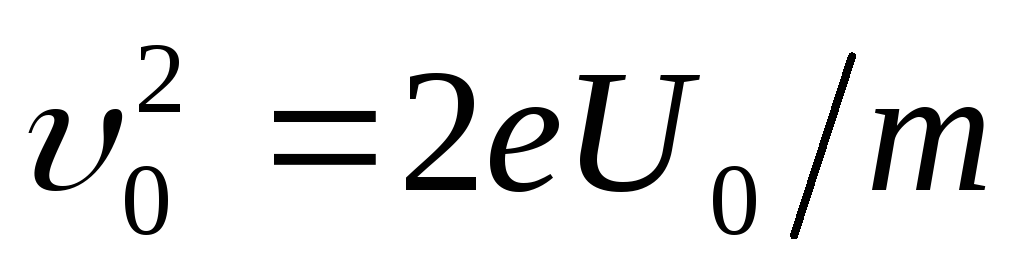(2)

Substituting in formula (1) consistently values but,F.T.and υ 0 2 from the corresponding expressions, we get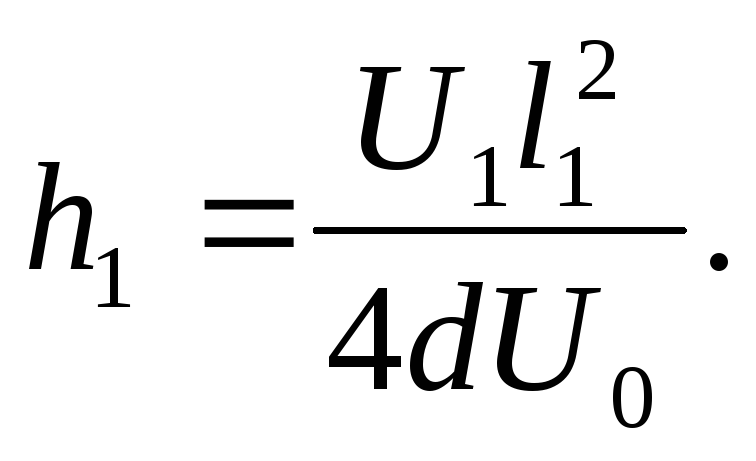

Length of cut h. 2 find from the similarity of triangles MDC.and stock vector

(3)

where υ 1 - electron speed in vertical direction at point M;l. 2 - distance from the condenser to the screen.

Speed υ 1 Find the formula υ 1 \u003d at,which, taking into account expressions for a, F.and t.take view

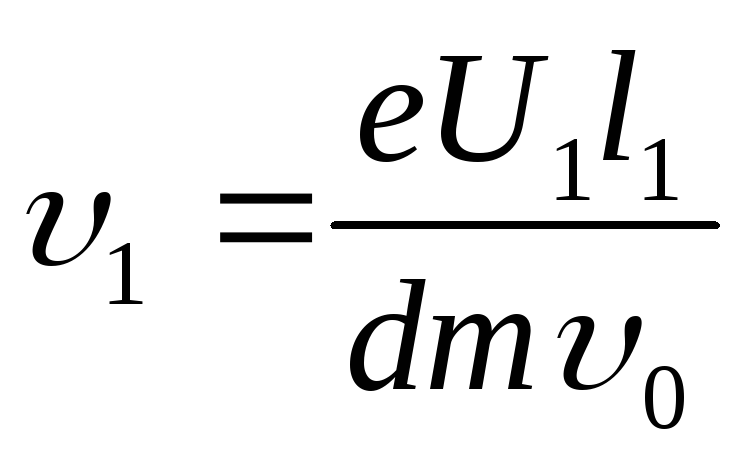
Substitting an expression υ 1 in formula (3), we get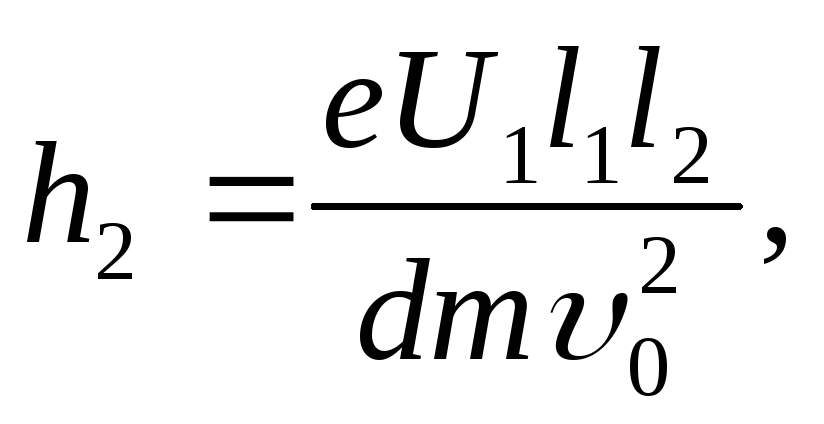

, or, replace υ 0 2 by formula (3), we will find

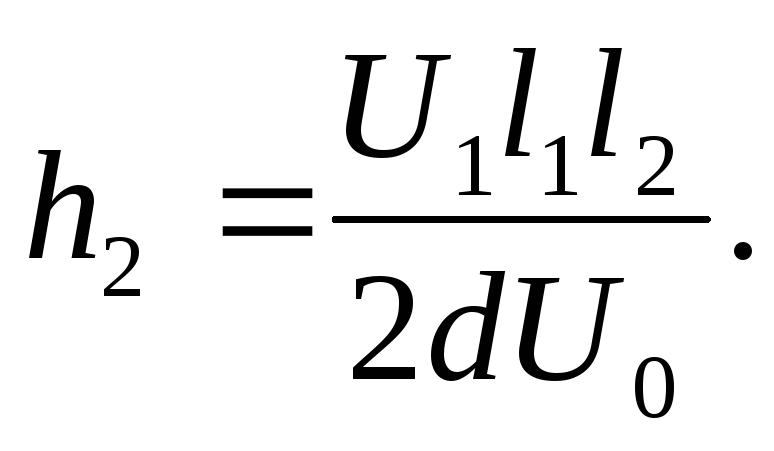
Finally for the desired distance | BC.| will have

|BC.|=

­

Substituting values U. 1 ,U. 0 ,d,l. 1 I. l. 2 In the last expression and making calculations, we get | BC.| \u003d 5.5cm.

Tasks

Potential energy and potential of spot charges

15.1. Point charge Q.\u003d 10 ND, being at some point of the field, has the potential energy n \u003d 10 μ5. Find the potential φ of this point of the field.

5.2. When moving charge Q \u003d 20.nGL between two field points by external forces was performed A \u003d 4.iCJ. Define work A. 1 field forces and the difference Δφ potentials of these field points.

15.3. Electrical field created by a point positive charge Q. 1 \u003d 6 ND. Positive charge Q. 2 is transferred from point BUTthis field to the point AT(Fig. 15.5). What is the change in the potential energy ΔP, entering the unit tolerable charge, if r. 1 \u003d 20 cm and r. 2 \u003d 50 cm?

15.4. Electric field created by point charge Q. L \u003d 50 ND. Without taking advantage of the concept of potential, calculate the work BUTat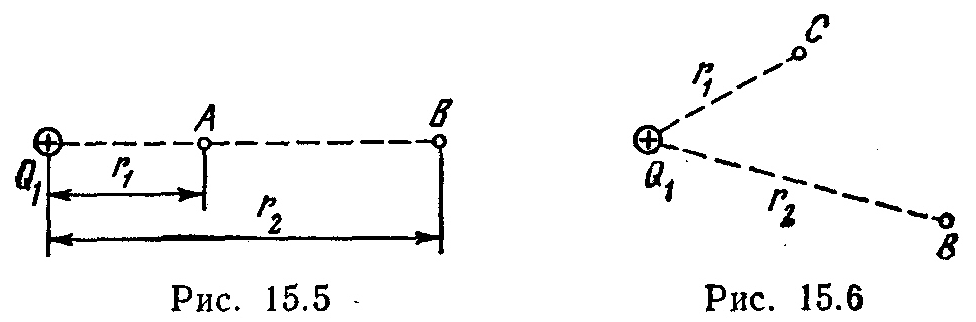

effective forces for moving point charge Q. 2 \u003d -2 NKL from point WITHexactly AT

(Fig. 15.6) if r. 1 =10 cm, r. 2 \u003d 20 cm. Determine also the change in the ΔP of the potential energy of the charge system.

15.5. The field is created by a point charge Q.\u003d 1 ND. Determine the potential of the φ field at a point removed from the charge r.\u003d 20 cm.

15.6. Determine the potential of φ of the electric field at a point removed from charges Q. 1 = -0.2 μKl I. Q. 2 =0,5 μKl, respectively, on r. 1 =15 mass media r. 2 \u003d 25 cm. Determine the minimum and maximum distances between charges in which the solution is possible.

15.7. Charges Q. 1 \u003d 1 μKl and Q. 2 = -1 μKl are at a distance d.\u003d 10 cm. Determine tension E.and the potential of the φ field at the point remote to the distance r.= 10 cm from the first charge and lying on the line passing through the first charge perpendicular to the direction from Q. 1 to Q. 2 .

15.8. Calculate the potential energy of the two-point charges Q. 1 \u003d 100 NDC and Q. 2 =10 nCL, located at a distance d.\u003d 10 cm from each other.

15.9. Find potential energy P systems of three point charges Q. 1 \u003d 10 ND, Q. 2 =20 nLK I. Q. 3 \u003d -30 NLLs located in the tops of the equilateral triangle with a side length a.\u003d 10 cm.

15.10. What potential energy P systems of four identical point charges Q.\u003d 10 ND, located in the vertices of the square with a side length but\u003d 10 cm? .

15.11. Identify the potential energy of the four-point charges of the four-point charges located in the vertices of the square with a side length a.\u003d 10 cm. Charges are the same module Q.\u003d 10 ND, but two of them are negative. Consider two possible cases of charges.

15.12 . The field was created by two point charges + 2Q.and -Q,distribution d.\u003d 12 cm from each other. Determine the geometric point of points on the plane for which the potential is zero (write the equation of the zero potential line).

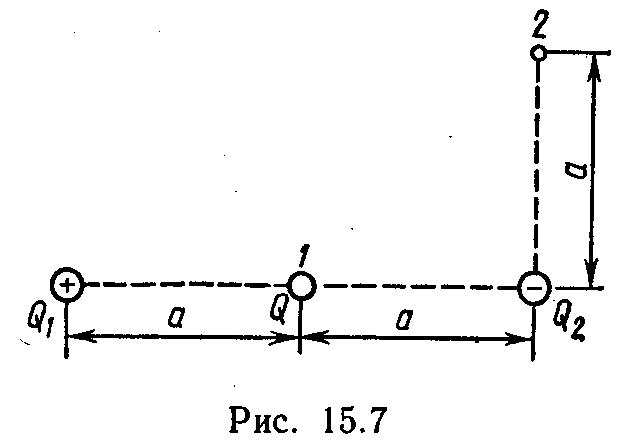
5.13. The system consists of three charges - two identical largest Q. 1 = |Q. 2 | \u003d 1 μKl and opposite by sign and charge Q \u003d 20.nKL, located point 1 in the middle between two other charges of the system (Fig. 15.7). Determine the change in the potential energy ΔP of the system when transferring the charge Q.from point 1 to point 2. These points are removed from the negative charge Q. 1 for distance a \u003d.0,2 m.

Potential of the field of linearly distributed charges

15.14. By thin ring radius R \u003d.10 cm is uniformly distributed with a linear density τ \u003d 10 nkl / m. Determine the potential φ at the point lying on the rings axis, at a distance a \u003d.5 cm from the center.

15.15. On the segment of a thin direct conductor is evenly distributed with a linear density τ \u003d 10 nkl / m. Calculate the potential φ created by this charge at a point located on the conductor axis and removed from the nearest end of the segment to the distance equal to the length of this segment.

The electrostatic field is potentially Coulomb forces - conservative forces, and the operation of conservative forces can be represented as a decrease of potential energy, i.e.

where C is a constant integration, which is usually selected so that when the charge Q is removed to infinity - W p \u003d 0, i.e. C \u003d 0.

We will explore the ESP using test charges Q Pr 1, Q Pr2, Q Pr 3 -

Potential electrostatic field called energy characteristic fields, numerically equal to potential test energy electric charge, placed at this point of the field, to the size of the charge.

Then, using relations (7.1) and (7.7) we obtain:

Knowing the distribution of charges, we can find the potential of the field of any system.

Potentials of fields folded algebraicallyTherefore, the calculation of potentials is usually simpler than the calculation of EP tensions.

In si unit of measurement of potential - [j] \u003d 1j / cl \u003d 1B

The unit of operation in 1 eV (electronic content) is equal to the work performed by the field for the charge equal to charge the electron, when the potential difference is passed to 1 V.

1 eV \u003d 1,6'10 -19 CL '1B \u003d 1,6'10 -19 J

Video Model: 1) The movement of charges in electric field; 2) mass spectrometer.

The body located in the potential field of forces (electrostatic field) has potential energy, due to which work is performed by the field. The work of conservative forces is made due to the loss of potential energy. Therefore, the work of the power of the electrostatic field can be represented as a difference of potential energies that possesses point charge Q. 0 In the initial and endpoints of the charge field Q.:, From where it follows that the potential energy charge q 0. in the charge field Q. equal . It is determined ambiguous, but with an accuracy of an arbitrary constant WITH. If we assume that when removing the charge in infinity ( r.® ¥) Potential energy refers to zero ( U.=0), that WITH\u003d 0 and potential charge energy Q. 0 , in the charge field Q. at a distance of g from it, equal . For the charges of the same name Q. 0 Q\u003e0 and the potential energy of their interaction (repulsion) is positive, for variemless charges Q. 0 Q.<0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.

Potential j. At any point of the electrostatic field there is a physical value determined by the potential energy of a single positive charge placed at this point. What follows that the potential of the field created by a point charge Q.equal. Work performed by the power of the electrostatic field when charging charge Q. 0 from the point 1 exactly 2 may be represented as, i.e. it is equal to the product of the transferred charge on the potential difference in the initial and end points. Potential difference Two points 1 and 2 The electrostatic field is determined by the work performed by the fields, when moving a single positive charge from the point 1 exactly 2 . Work forces of the field when traveling charge Q. 0 from the point 1 exactly 2 can also be recorded as . The expression for the potential difference: where integration can be performed along any line connecting the initial and endpoints, since the operation of the power of the electrostatic field does not depend on the movement path.

If you move the charge Q. 0 from an arbitrary point beyond the field, i.e., in infinity, where, by condition, the potential is zero, then the work of the power of the electrostatic field A. ¥ \u003d Q. 0 j.from

Potential - The physical quantity determined by the work on the movement of a single positive charge when it is removed from this field of the field to infinity. This work is numerically equal to the work performed by external forces (against the power of the electrostatic field) to move a single positive charge from infinity at this field point. Capacity Unit - volt (C): 1 in there is the potential of such a point of the field in which the charge of 1 CL has a potential energy of 1 J (1 V = 1 J / CL).

In the case of an electrostatic field, the potential energy is the measure of the interaction of charges. Suppose in space there is a system of point charges Q I.(i. = 1, 2, ... ,n.). Easiness of all n. charges will determine the relationship

where r IJ -the distance between the corresponding charges, and the summation is made in such a way that the interaction between each pair of charges is taken into account once.

From this it follows that the potential of the field of charge system is equal algebraic The sum of the potentials of the fields of all these charges:

Considering the electric field created by the charge system, it is necessary to use the superposition principle to determine the field potential:

The potential of the electrical field of the charge system at a given point of the space is equal to the algebraic sum of the potentials of electric fields created at this point of space, each charge of the system separately:

6. Equipotential surfaces and their properties. Communication between the potential difference and tension of the electrostatic field.
Imaginary surface, all points of which have the same potential, is called an equipotential surface. Equation of this surface

If the field is created by a point charge, then its potential Thus, the equipotential surfaces in this case are concentric spheres. On the other hand, the line of tension in the event of a point charge is radial straight. Consequently, tension lines in the case of a point charge perpendicular Equipotential surfaces.

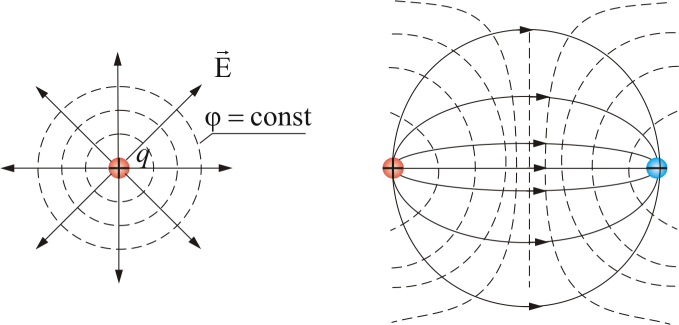
All points of the equipotential surface have the same potential, so work on the movement of the charge along this surface is zero, i.e. the electrostatic forces acting on the charge is always Aimed according to standards to equipotential surfaces. Consequently, vector E. always normal to equipotential surfaces, and therefore the lines of the vector E. orthogonal these surfaces.

Evipotential surfaces around each charge and each charge system can be held countless. However, they are usually carried out so that the potential differences between any two neighboring equipotential surfaces were the same. Then the density of the equipotential surfaces clearly characterizes the field strength at different points. Where these surfaces are ground, the field strength is greater.

So, knowing the location of the tension lines of the electrostatic field, you can construct equipotential surfaces and, on the contrary, at a reasonable location of the equipotential surfaces, you can determine the module and direction of the field strength at each point.

We will find the relationship between the tension of the electrostatic field, which is force characteristic and potential - energy characteristic field.

Work on moving single point positive charge from one point of the field to another along the axis h. provided that the points are located infinitely close to each other and x. 2 -X. 1 = d. x equal E X.d. x. The same work is equal j. 1 -J. 2 \u003d DJ.Equating both expressions, we can record

where the character of the private derivative emphasizes that differentiation is performed only by x. Repeating similar arguments for the axes w. and z, We can find vector E.:

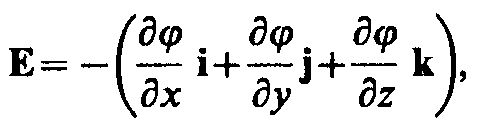
where i, J, K - single vectors of coordinate axes x, y, z.

From the definition of the gradient it follows that

i.e. tension E. The fields are equal to the potential gradient with a minus sign. The minus sign is determined by the fact that the vector of tension E. Fields sent to B. side of descendingpotential.

For a graphic image of the distribution of the potential of the electrostatic field, as in the case of a field of gravity, use equipotential surfaces - surfaces, in all points of which the potential j. It has the same meaning.