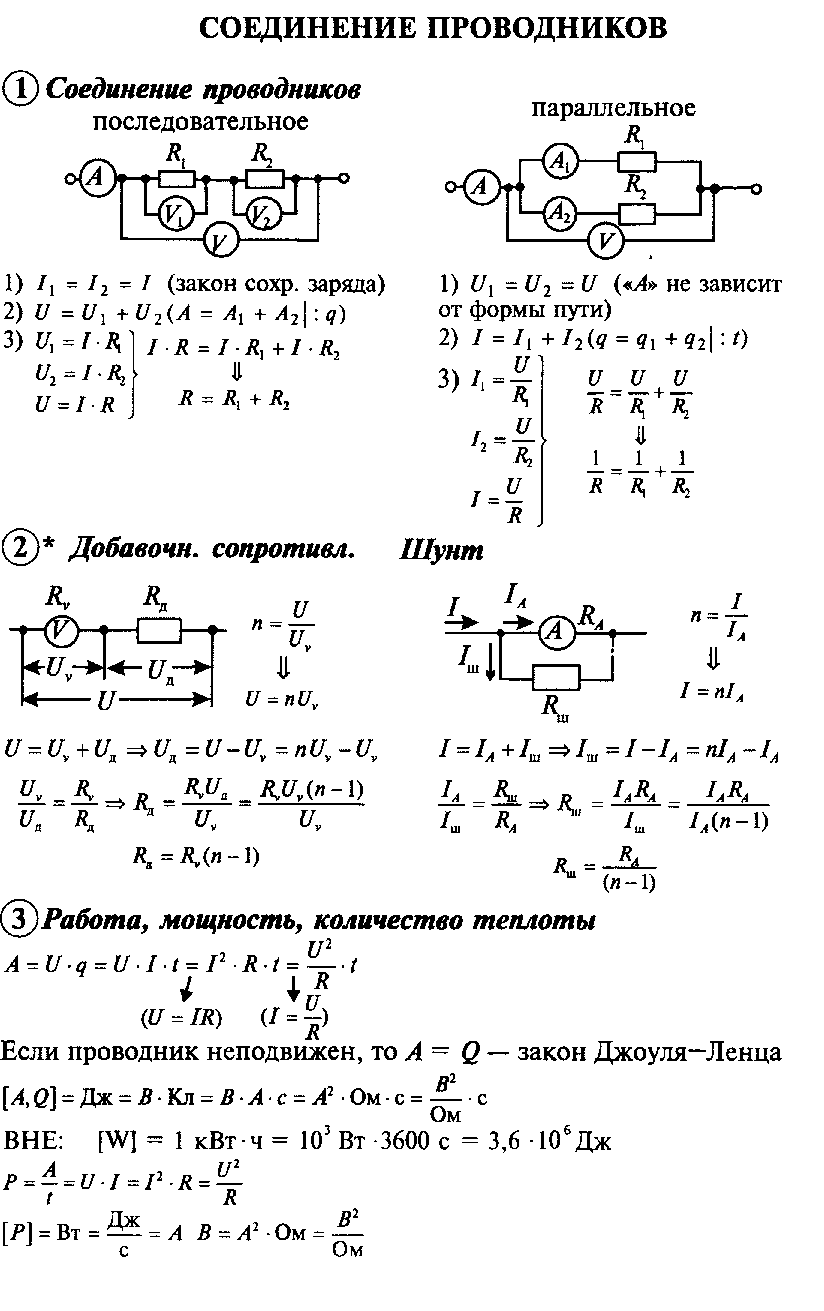
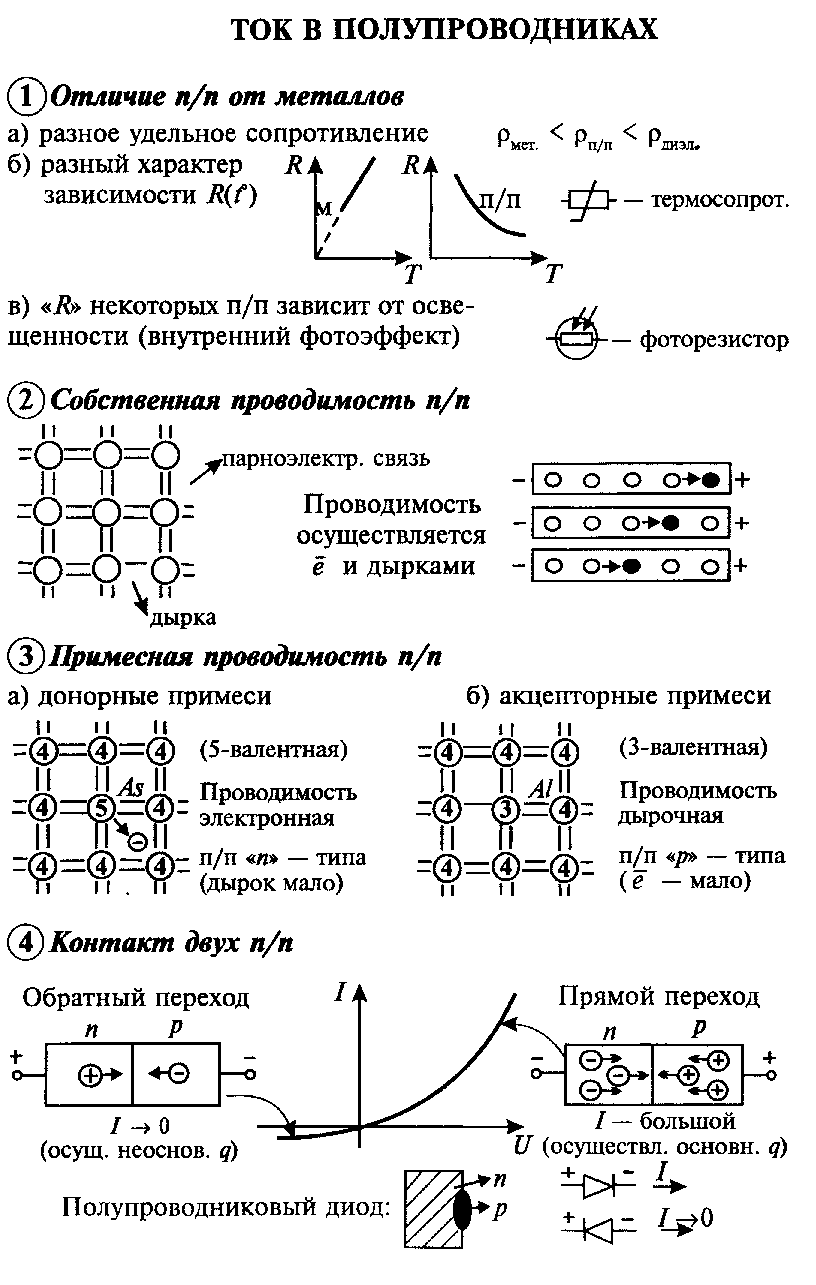
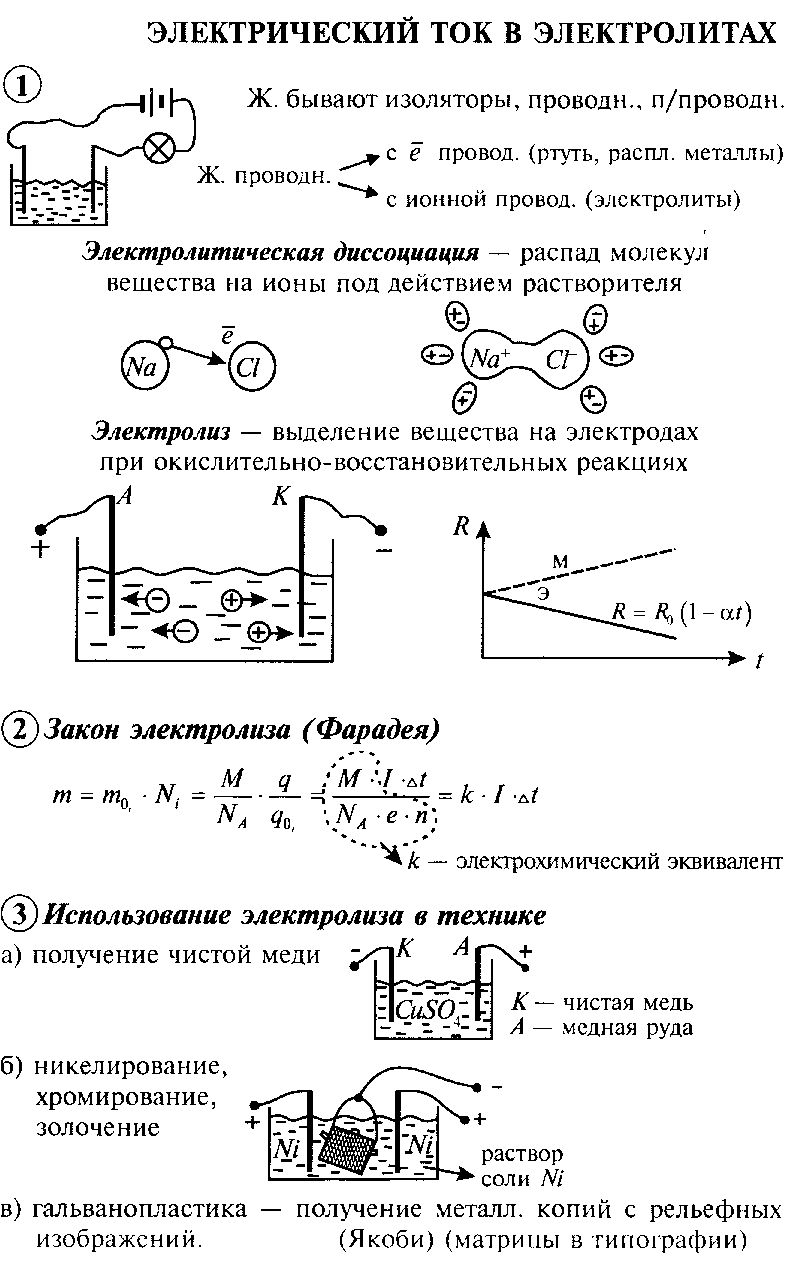
Charged bodies attract or repel each other. When moving charged bodies, for example, the leaflets of the electroscope, the forces acting between them make work. It is known from the mechanics that the system capable of doing work due to the interaction of the Tellian with a friend has potential energy. It means that the system of charged bodies has the potential energy called electrostaticor electric.
The concept of potential energy self-hidden in electrostatics. Remember how difficult it was to imagine what potential energy in the mechanics. We feel the power directly, but there are no potential energy. On the fifth floor of the house, the potential energy of issor is more than on the first. But we do not perceive it.
The difference becomes clear if you remember that when the upward lifting it was necessary to work, as well as, if you imagine what would happen when falling from the fifth floor.
The energy of the interaction of electrons with the nucleus in the atom and the energy of the interaction of atoms with each other in molecules (chemical energy) is mainly electric Energy. Huge electrical energy is stored inside the atomic nucleus. It is due to this energy that the heat is distinguished when the nuclear reactor of the nuclear power plant is released.
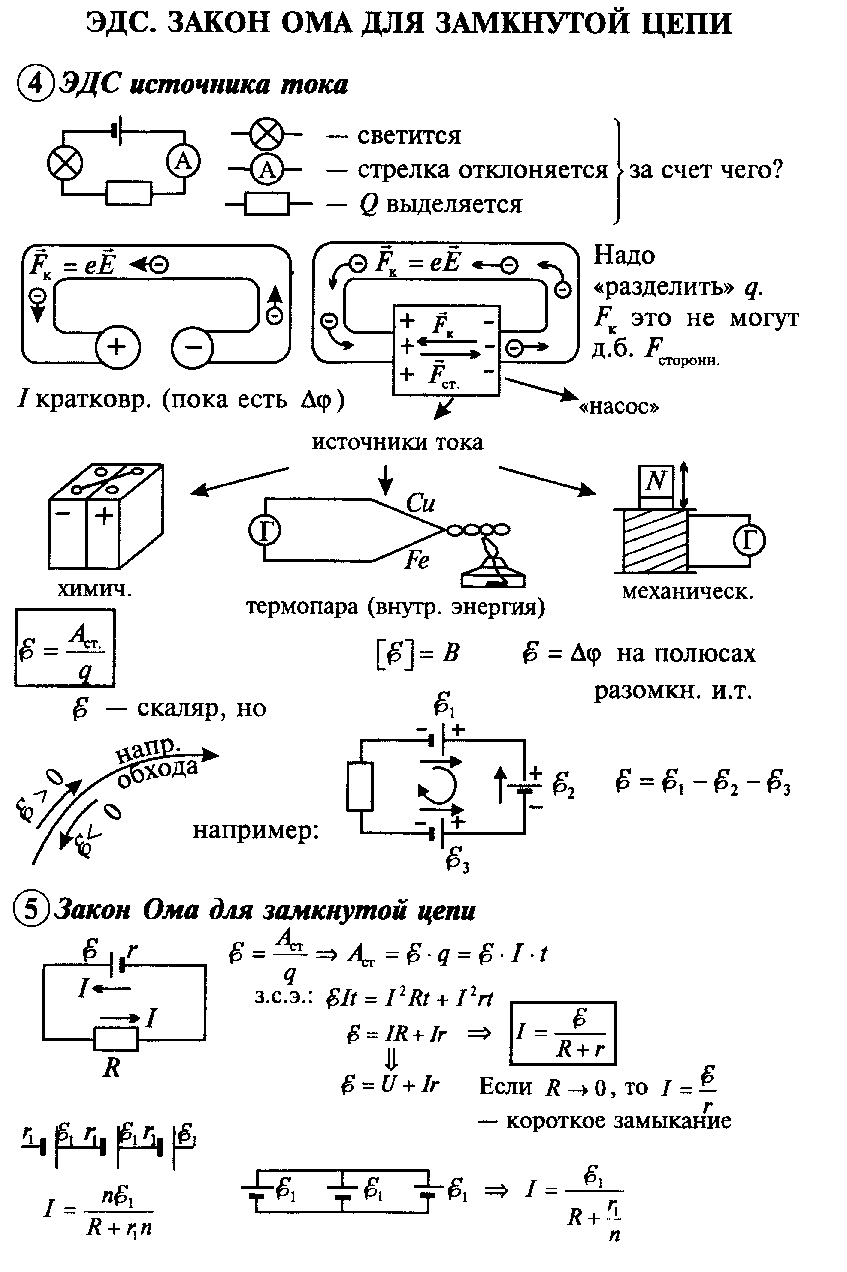
From the point of view of the theory of close to the charge, the electrical field created by another charge is directly applied. When charging the charge acting on it from the side of the field, the force makes work. (In the future, we will simply talk about the work of the field.) Therefore, it can be argued that the charged body in the electric field has energy. We find the potential charge energy in homogeneous electric field.
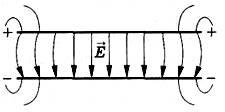
Work when moving the charge in a homogeneous electrostatic field.The homogeneous field is created, for example, large metal plates, having the charges of the opposite sign. This field acts on the charge with constant power. ,
just as the land acts with constant force F \u003d Mg.on the stone near her surface. Let the plates are located vertically (Fig. 1), the left plate INcharged negatively, and right D.- positive. Calculate the work performed by the field when moving positive charge q.from point 1, located at a distance d 1.from plate IN,exactly 2,
located at a distance d 2.
On the station site Δd \u003d d 1 -D 2the electric field will make positive operation:
This work does not depend on the form of the trajectory, just as it does not depend on the form of the trajectory work of gravity. Let us prove it with direct calculation.
We calculate the work when the charge is moving along an arbitrary curve connecting points 1 and 2 . Moving along a smooth curve can be replaced by movement along a step line with an arbitrarily small steps (Fig. 2). When moving along steps, perpendicular field strength E,work is not performed. On the steps and parallel E,work is done (f. 1), since the sum of the lengths of horizontal segments is equal Δd \u003d d 1 -D 2.
Potential energy. If the work does not depend on the form of the trajectory, it is equal to the change in the potential energy taken with the opposite sign:
This was discussed in detail in the course of the physics of the IX class.
Comparing the resulting expression (F. 1) with a general definition of potential energy (f. 2), we see that potential charge energy in a homogeneous electrostatic fieldequal to:
Formula (F.3) is similar to the formula W p \u003d mghfor the potential energy of the body above the ground surface. But the charge q.in contrast, the mass can be both positive and negative.
If the field makes positive operation, the potential energy of the charged body in the field decreases: ΔW P<0. Одновременно согласно закону сохранения энергии растет его кинетическая энергия. На этом основано ускорение электронов электрическим полем в электронных лампах, телевизионных трубках и т. д. И наоборот, если работа отрицательна (например, при движении положительно заряженной частицы в направлении, противоположном направлению напряженности поля ; this movement is similar to the movement of the stone thrown up), then ΔW p\u003e 0. Potential energy is growing, and kinetic energy decreases; The particle is braked.
On a closed trajectory, when the charge returns to the starting point, the field operation is zero:
Zero level of potential energy.Potential energy (see formula (3)) equal to zero on the surface of the plate IN. This means that the zero level of potential energy coincides with the plate IN.But, as in the case of the forces of gravity, the zero level of potential energy is chosen arbitrarily. We can assume that W p \u003d 0on distance d 2.from plate IN,Then
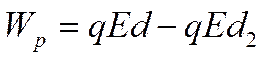
The physical meaning is not the potential energy itself, but the difference of its values, determined by the operation of the field when the charge is moved from the initial position to the final.
Charged particles in the electrostatic field have potential energy. When moving a particle from one point of the field to another electric field makes a job that does not depend on the form of the trajectory. This work is equal to the change in the potential energy taken with the "minus" sign.
We will start with the discussion of the potential energy, which is charged in the electrostatic field. First of all, it is necessary to remember under what conditions you can generally introduce the concept of potential energy.
4.1 Conservative power
The force is called conservative (or potential) if the work of this force does not depend on the form of the trajectory and is determined only by the initial and ending position of the body.
Let, for example, the body under the action of the conservative force ~ moved from the initial
points 1 to the end point 2 (Fig. 16). Then the work of strength ~ depends only on the situation
points themselves 1 and 2, but not from the trajectory of the body movement. For example, for trajectories 1! A! 2 and 1! B! 2 The value A will be the same.
Fig. 16. To the concept of conservative power
Note that the operation of the conservative force on any closed path is zero. Indeed, let's get out of point 1 along the trajectory 1! A! 2 and go back on the trajectory 2! B! 1. On the first trajectory, the force will work A, and on the second trajectory work will be equal to A. In the end, the total work will be zero.
So, the concept of potential energy can be administered only in the case of conservative power. The potential energy W is a mathematical expression depending on the coordinates of the body, such that the work of the force is equal to the change in this expression with a minus sign:
Or, what is the same:
A \u003d (W2 W1) \u003d W1 W2:
As you can see, the operation of the conservative strength is the difference between the values \u200b\u200bof the potential energy calculated accordingly for the initial and final positions of the body.
Examples of conservative forces are well known for you. For example, gravity is conservative. The strength of the spring is also conservative. That is why we can talk about the potential energy of the body raised above the earth, or the potential energy of the deformed spring.
But the friction force is not conservative: the work of friction force depends on the form of the trajectory and is not equal to zero on the closed path. Therefore, there is no ¾Potential body energy in the friction force field.
![]()
4.2 Potentialness of the electrostatic field
It turns out that the force with which the electrostatic field acts on the charged body is also conservative. The work of this force committed when moving the charge is called work electrostatic field. We have, thus, the most important fact:
The operation of the electrostatic field does not depend on the form of the trajectory, which moves the charge, and is determined only by the initial and ending position positions. The field of the closed pathway is zero.
This fact is also called the potential of the electrostatic field. Like the field of gravity, the electrostatic field is potential. The operation of the electrostatic field is the same for all paths for which the charge can move from one fixed point of space to another.
Strict mathematical proof of the potentiality of the electrostatic field is beyond the scope of the school program. However, the physical level of the rigor can be verified in the justice of this fact using the next simple reasoning.
It is not difficult to see that if the electrostatic field was not potential, you could build an eternal engine! In fact, then there would be a closed trajectory, when moving the charge on which the field would have made positive work (and at the same time no changes in the surrounding bodies would have happened). We turn yourself the charge for this trajectory, draw an unlimited amount of energy nowhere and all the energy problems of humanity are solved :-) But such, alas, it is not observed this blatant contrary to the law of energy conservation.
Since the electrostatic field is potentially, we can talk about the potential energy of charge in this field. Let's start with a simple and important case.
4.3 Potential charge energy in a uniform field
The potential body energy raised above the earth is equal to MGH. The charge case in a homogeneous field turns out to be very similar to this mechanical situation.
Consider a homogeneous electrostatic field E, the voltage line of which is directed along the X axis (Fig. 17). Let the positive charge Q move along the power line from point 1 (with the x1 coordinate) to point 2 (with the coordinate x2).
0 x 1. | |||
Fig. 17. Move charge in a uniform field
The field acts on the charge with force ~, which is directed along the voltage lines. Work
this force, how easy it is to see, will be equal to:
A \u003d f (x2 x1) \u003d Qe (x2 x1):

What will change if points 1 and 2 do not lie on one line of tension? It turns out nothing! The formula for the field of operation will remain the same. Make sure this with the help of Fig. eighteen .
0 x 1. | ||||
Fig. 18. Moving the charge in a uniform field
Moving from point 1 to point 2, let's choose the path 1!3! 2, where point 3 lies on one power line with a point 1. Then the operation of the A32 on the section 32 is zero because we move perpendicular to the strength. As a result, we get:
A \u003d A13 + A32 \u003d A13 \u003d QE (x2 x1):
We see that the operation of the field depends only on the abscissa of the initial and final charge provisions. We write the resulting formula as follows:
A \u003d QEX2 QEX1 \u003d ((QEX2) (QEX1)) \u003d (W2 W1) \u003d W:
Here W1 \u003d QEX1, W2 \u003d QEX2. The operation of the field, in accordance with formula (8), it turns out to be equal to a change with a minus size mark
This value is the potential charge energy in a homogeneous electrostatic field. Through X, the abscissa point is indicated in which potential energy is searched. The zero level of potential energy in this case corresponds to the beginning of the coordinates x \u003d 0 and in the figures is depicted by a dotted line, perpendicular to the tension lines4.
Recall that it is considered q\u003e 0. From formula (9) it follows that when the charge is moved along the power line, the potential energy decreases with increasing x. This is natural: after all, the field makes positive work, accelerating the charge, and kinetic energy The charge is growing at the expense of loss of its potential energy.
It is easy to show that Formula (9) remains fair and for Q< 0. В этом случае потенциальная энергия возрастает с ростом x. Это тоже понятно: ведь сила, с которой поле действует на заряд, теперь будет направлена влево, так что движение заряда вправо будет осуществляться против действия поля. Заряд тормозится полем, кинетическая энергия заряда уменьшается, а потенциальная энергия увеличивается.
So, important conclusion: in the formula for potential energy through q is the algebraic charge value (taking into account the sign), and not its module.
4 In fact, the zero level of potential energy can be selected anywhere. In other words, the potential energy is determined only with an accuracy of an arbitrary additive constant C, i.e. w \u003d qex + c. There is nothing terrible in such uncertainty: the physical meaning has the potential energy itself, and the difference in potential energies, equal work Fields. In this difference, the C constant will be reduced.
4.4 Potential energy interaction of point charges
Let two point charges Q1 and Q2 are in vacuo at a distance of r from each other. It can be shown that the potential energy of their interaction is given by the formula:
kQ1 Q2. | ||||
We accept formula (10) without proof. Two features of this formula should be discussed.
First, where is the zero level of potential energy? After all, the potential energy, as can be seen from the formula (10), cannot appeal to zero. But in fact, the zero level exists, and he is in infinity. In other words, when charges are located infinitely far from each other, the potential energy of their interaction is supposed to be zero (which is logical in this case, the charges are already interacting.
Secondly, Q1 and Q2 is again the algebraic values \u200b\u200bof charges, i.e. charges taking into account their sign.
For example, the potential energy of the interaction of the two charges of the same name will be positive. Why? If we let them go, they will start accelerate and remove each other. Their kinetic energy increases, the potential energy decreases. But at infinity, the potential energy is drawn to zero, and since it decreases to zero, it means it is positive.
But the potential energy of the interaction of the distinct charges is negative. Indeed, let's remove them on a very long distance from each other so that the potential energy is zero and let go. The charges will begin accelerate, approaching, and the potential energy decreases again. But if she was zero, then where does she lose? Only towards negative values.
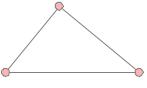
Formula (10) also helps to calculate the potential energy of the charges system, if the number of charges are more than two. To do this, you need to sum up the energies of each pair of charges. We will not write a general formula; We better illustrate the said simple example shown in Fig.19.
Fig. 19. The interaction of three charges
If the charges q1, q2, q3 are in the vertices of the triangle with the sides of A, B, C, the potential energy of their interaction is equal to:
kQ1 Q2. | kQ2 Q3. | kQ1 Q3. | |||||
4.5 Potential
From formula W \u003d QEX, we see that the potential energy of charge Q in a uniform field is directly proportional to this charge.
The same we see from the formula w \u003d kq1 q2 \u003d r: The potential charge energy Q1, which is in the field of point charge Q2, is directly proportional to the charge value Q1.
The work of the conservative forces is equal to the change in the potential energy taken with the opposite sign, that is, a \u003d -dw n \u003d - (W p2 -w p1) \u003d -qe (ℓ 2 - ℓ 1). Consequently, in a homogeneous electrostatic field, the potential energy of charge W p \u003d Qe ℓ, where ℓ is the shortest charge distance from the beginning of the reference.
The potential charge energy in the electrostatic field is proportional to the charge. This is true not only for homogeneous, but also for any electrostatic field. Therefore, the ratio of the potential energy of the charge, placed in any point of the electrostatic field, the value of this charge does not depend on the charge, but is the characteristic of the field at this point, it is called electric potential j At this point j \u003d w p / q.
The potential of the electrostatic field at this point is scalar value, numerically equal to the potential energy of a single charge placed at this point of the field. The potential is energy characteristic Fields, i.e. Energy charge at the point of the Potential J: W p \u003d QJ.
Charging Travel Field A \u003d - (W p2 - w p1) \u003d -q (J 2 - J 1) \u003d QDJ
Magnitude DJ. = j 1 - J 2call the difference in potentials. Potential unit 1B \u003d 1J / 1kl potential difference.
The potential at this point of the electrostatic field can be determined only with an accuracy of a certain constant value, the numeric value of which depends on the choice of the origin of the potential. When transferring the beginning of reference, the potentials of all points of the electrostatic field are changed to the same value, and the potential difference remains unchanged. The work of the charge movement in the electrostatic field depends on the potential difference, therefore it is indifferent to its counting, where the beginning of the countdown of the potential was selected.
Therefore, to choose the beginning of the reference potential can be arbitrarily. In theoretical calculations, the potentials of infinitely remote points are taken equal to zero. In electrical and radio engineering, the surface of the earth takes the surface of the potential.
The potential of the electrostatic field created by a point electrical charge is determined at this point by the formula.
The potentials of the points of the field created by a point positive charge are positive and decrease by removing from it, and in the field of the negative point charge, the potentials are negative and increase when removing the charge. In case, for zero, the potential of infinitely remote points is adopted, the potential of the point charge field has a simple physical meaning: that is, the potential of this point of the electrostatic field created by a point charge, numerically equal to workaccomplished by the force acting on the side of the field, when moving a single positive charge from this point in an infinitely remote.
The formula is also valid for determining the potential at the points of the field created by a uniformly charged sphere or a ball at distances, large or equal to its radius, since the field of such a sphere is out of it and on its surface coincides with the point charge field.
If the charge is not point, then to determine the potential of the field created by them, are applied as follows. Smash this charge at arbitrarily small charges, each of which can be considered point. Then the potential at an arbitrary point of the field will be determined as the amount of potentials created at this point by each individual point charge, i.e.
Surface, all points of which have the same potential, called equipotential. For example, in the field of point charge, the equipotential are surfaces of spheres described around this charge with the center at the point where it is located.
The intersection of equipotential surfaces with the drawing plane forms the equipotential lines. With their help, we can graphically portray the electric field, just as we did with tension lines.
The line of tension of the electrostatic field is directed perpendicular to equipotential surfaces and show the direction of the greatest decrease in potential. Therefore, when the charge is moving along the equipotential surface electric power work do not commit, i.e. Work is zero.
Work when moving the charge in a homogeneous field perpendicular to the equipotential surfaces ![]() - in a homogeneous field.
- in a homogeneous field.
We calculate the potential energy of electrical charges for the simplest, but very important special cases.
The potential energy of the charge in a homogeneous field let the charge q move in a homogeneous electric field with a strength e from point 1 to point 2. Position of point 1 is determined by the radius-vector and point 2 by the radius-vector G2. Acting force F \u003d QE constant. The operation of force F does not depend on the form of the trajectory connecting points 1 and 2. This follows from the overall proof of the potentiality of the electrostatic field. It is possible to conduct evidence and with the help of directly calculating the work when moving the charge on different ways in the same way as was done in "Mechanics" for gravitational forces. Now we will not do this.
The easiest way to calculate the work if the charge moves along a straight line connecting point 1 and point 2 (Fig. 1.78). Vector of displacement DG \u003d G2 - RV Work is equal to the scalar product for movement:
A \u003d f Ar ^ Qe (R2-R1) \u003d QE R2-QE GG (1.18.1)
On the other hand, according to (1.17.1), A \u003d ~ (W 2 ~ comparing expressions (1.18.1) and (1.17.1), we obtain an expression for the potential energy of charge in a uniform field:
WP ~ -qe G. (1.18.2)
The homogeneous field is created, in particular, in space between parallel plates that carry the charges of opposite characters (Fig. 1.79). Naturally choose the coordinate system so that the X axis is directed perpendicular to the plates. Then projections e "and e, equal to zero and expressing
z.
niє (1.18.2) acquires the form:
WP \u003d -Q (EXX + EUU + EZZ) \u003d ~ QEXX. (1.18.3)
Formula (1.18.3) is similar to the formula WP \u003d MGH for the potential energy of the body above the surface of the Earth. The role of the mass is played by the charge, accelerating the free fall - the field strength, and instead of the height h stands the coordinate x. But the energy sign is different: minus instead of the plus. The point here is what. The mass is always positive, and the force of gravity is necessarily directed vertically down. Taking into account these circumstances, the formula WP \u003d MGH was recorded. It has a module for accelerating the free fall, and the height H is counted from the ground surface. Formula (1.18.3) is more general. Charge Q can be both positive and negative; The field strength can be sent anywhere, and its projection can have both a positive value and a negative depending on the choice of coordinate system.
In particular, if the field strength e is directed vertically down, and the axis is up, then
WP \u003d QE \\ X \\ (1.18.4)
in accurately, according to the expression WP \u003d MGH.
If the electric field makes positive operation, then the energy of the charged body in the field decreases: AW 0. Such movement of the charged particle is similar to the movement of the stone thrown up. The potential particle energy is growing, and kinetic energy decreases: the particle is inhibited.
Zero level of potential energy
The potential energy in electrodynamics is determined, as in mechanics, with an accuracy of an arbitrary constant. Instead of expression (1.18.2), we could write:
W \u003d -qe-R + C, (1.18.5)
where C is an arbitrary constant. In this case, the change in the potential energy remains the same, and the work determines the change in the potential energy, and not the energy itself. Recording formula (1.18.2), we actually equated constant with to zero. This corresponds to a certain choice of zero level of potential energy. For example, for the case shown in Figure 1.79, the potential energy is considered equal to zero on the surface of the plate B. But, as under the action of the forces of grave, the zero level of potential energy is chosen arbitrarily. We can assume that W - oh at a distance from the plate.
WP \u003d -QEXX-QEXX
The physical meaning is not the potential energy itself, but the difference of its values, determined by the operation of the field when the charge is moved from the initial position to the final.
Energy interaction spot charges
In the course of mechanics, an expression was obtained for the energy of the interaction of point bodies:
tI and "W \u003d -G ---.
R G.
If, instead of point masses, take two variepetes on the charge sign Q1 and Q2 (charges are attracted), then you can get a similar expression for the potential energy of their interaction:
w (1.18.6)
R G y "
For charges of one sign (charges repel) the sign of potential energy will be the opposite:
w (1.18.7)
R G y "
Formulas (1.18.6) and (1.18.7) can be combined into one if instead of the charge modules take their algebraic values:
W. (1.18.8)
PG V "
The sign of potential energy will automatically turn out to be high.
If the charges Ql and Q2 have the same signs, the potential energy of their interaction is positive (Fig. 1.80, a). It is the greater the less distance between charges, as the work that Coulomb forces can make when repulsing charges from each other will be more. If the charges have opposite signs, the energy is negative and the maximum value equal to zero is achieved at r -\u003e oo (Fig. 1.80, b). The more g, the greatest work will make the strength of attraction under the rapprochement of charges.
Fig. 1.80
When recording potential energy in the form (1.18.8), a certain choice of zero level of potential energy has already been made. It is believed that the potential energy of infinitely remote charges is zero: WP - "0 at r -" oo. Such a choice of zero level is convenient, but not required. Instead of expression (1.18.8) could be written with the same success that
(1.18.9)
r G y "
where C is an arbitrary constant. It can be seen that the positive or negative value of the potential energy of special physical meaning has no meaning. The sign of potential energy will be defined when fixing an arbitrary constant C. By changing the value of C, we can change the WP sign at a given distance g between charges.
Potential energy of a dot charge system
The potential energy of the dot charge system QV Q2, ..., Qn is equal to the sum of the potential energies of all pairs of mutual modest charges. For three charges
w KBSI + HBS * + HWZ L
R G1,2 g1.3 g2.3
Prove it yourself using the next reception. Initially, the charges Q2 and QZ are at an infinitely large distance from charge QV. Then charge Q2 moves to the point at a distance of GL 2 from the first charge. Following the charge qz moves to a point at a distance of G1 3 from the first charge and G2 3 from the second. It is necessary to calculate the work of the Coulomb forces committed with these movements, and equate its change in the potential energy taken with the opposite sign.
In the general case of n charges
N N.
WP \u003d I LLK7RH\u003e (1.18.11)
i \u003d lfc \u003d l (I * k)
where r; k - the distance between the charges of the Ink numbers. Coeffi - 1.
cien 2 is due to the fact that when summing, the potential energy is taken into account twice as the same
Ri, k rk, i
Potential Energy Formulas electric charge In a homogeneous field (1.18.2) and for two point charges (1.18.8), it is advisable to remember. They will meet quite often.
? 1. Is it possible to create electrostatic
le, whose tension lines paral- ^^^^^^^^
lelins, and the tension module
in the direction perpendicular to
remens (Fig. 1.81)? Fig. 1.81.
Draw a graph of the dependence of the potential energy of multi-charged particles from the distance, provided that the arbitrary constant C in formula (1.18.9) is positive.
How will formula look like (1.18.8) if the charges are located in a dielectric constant є?
Build an accurate picture of the power lines of the charged body - a difficult task. You must first calculate the field strength e (x, y, z) as the function of coordinates. But this is still not enough. There remains the difficult task of conducting continuous lines so that at each point of the line the tangent to it coincides with the direction of tension. Such a task is the easiest way to charge a computer running on a special program.
However, it is not always necessary to build an accurate picture of the distribution of force lines. Sometimes it is enough to draw close pictures, not forgetting that:
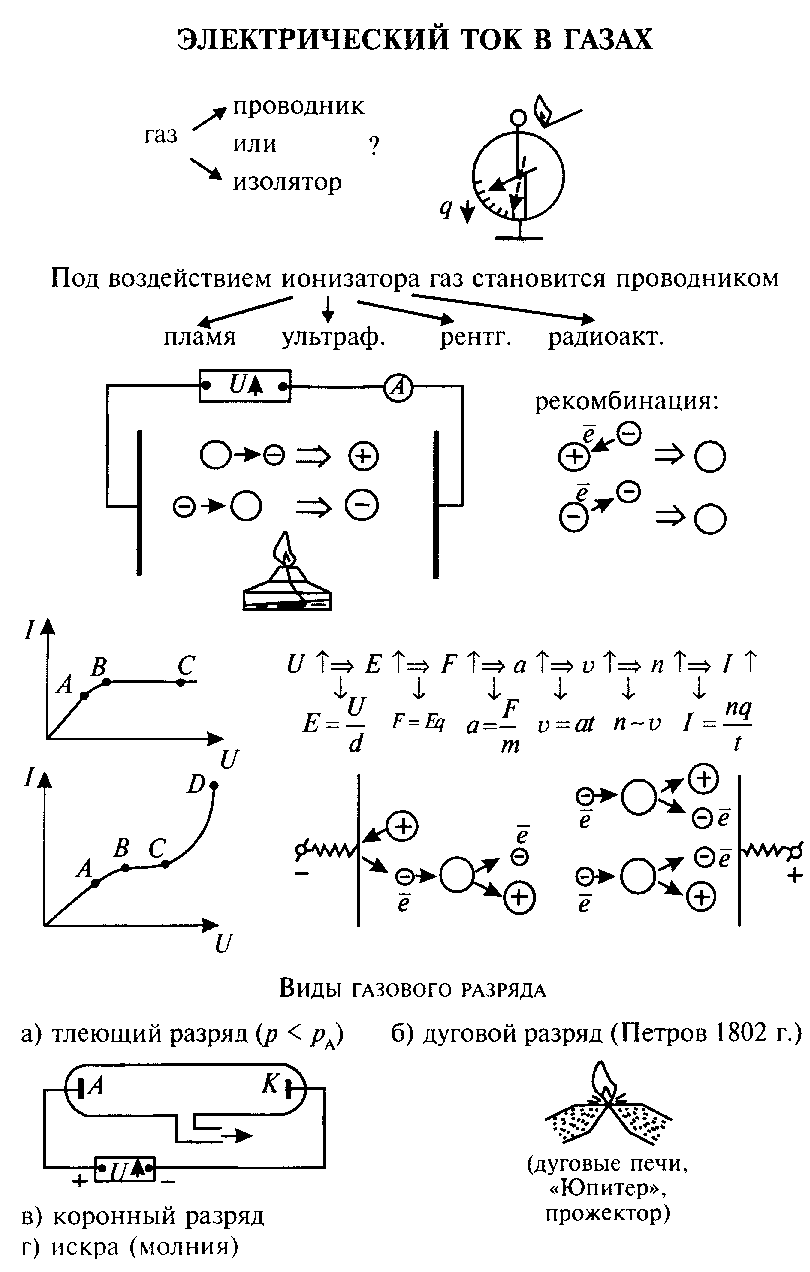
power lines are unlocked lines: they begin on the surface of positively charged bodies (or in infinity) and ends on the surface of negatively charged bodies (or in infinity);
the power lines do not intersect, since at each point of the field, the vector of tension has only one direction;
between charges power lines Nowhere are not interrupted.
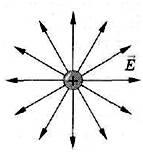
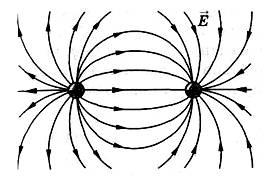
Figures 7-10 show patterns of force lines: a positively charged ball (Fig. 7); two variemlessly charged balls (Fig. 8); two simply charged balls (Fig. 9); Two plates whose charges are equal to the module and are opposite to the sign (Fig. 10).
|
|
|
|
|
|
Figure 10 shows that in the space between the plates, the power lines are far from the edges parallel: the electric field here is the same at all points.
Electric field whose tension is the same in all points of space, called uniform.


Work when moving the charge in a homogeneous electrostatic field. The homogeneous field is created, for example, large parallel metal plates having charges of the opposite sign. This field is valid for the charge. q. with constant power F. = qE, just as the land acts with constant force F. = mG. on the stone near her surface.
Let the plates are located vertically (Fig. 2), the left plate charged positively, and right - negatively calculate the work performed by the field when moving a positive charge q. from the point 1, located at a distance d. x. from the left plate, to the point 2, located at a distance d. 2 from her.
Points 1 and 2.lying on one power line:
A \u003d.qE (D 1 - d. 2 ) = qE∆ d.. (1)
This work does not depend on the form of the trajectory, just as does not depend on the form of the trajectory work of gravity.
Potential energy. Since the operation of electrostatic force does not depend on the form of the trajectory of the point of its application, this force is conservative, and its work according to the formula is equal to the change in potential energy taken with the opposite sign:
A. = -(W. n. 2 - W. nL. ) = -∆ W. n. .
Comparing the resulting expression with the general definition of potential energy, we see that the potential energy of charge in a homogeneous electrostatic field is equal to:
W. n. = qED.
If the field makes positive work, the potential energy of the charged body in the field decreases: ∆ W. n. < O. At the same time, according to the law of energy conservation, its kinetic energy is growing. And vice versa, if the work is negative (for example, when moving a positively charged particle in the direction opposite to the direction of the field strength vector E.T. ∆ W. n. > 0. Potential energy is growing, and the kinetic energy decreases, the particle is inhibited.
On a closed trajectory, when the charge returns to the starting point, the field operation is zero:
A. = -∆ W. n. = -(W. nL. - W. n. 2 ) = 0.
Charged particles in the electrostatic field have potential energy. When moving a particle from one point of the field to another electric field makes a job that does not depend on the form of the trajectory. This work is equal to the change in the potential energy taken with the sign "-".
In the mechanics, the mutual effect of bodies is characterized by force and potential energy. The electrostatic field carrying out the interaction between charges is also characterized by two values. Field tension is power characteristic.Now we introduce the energy characteristic - the potential.
Potential field.The operation of any electrostatic field when the charged body moves in it from one point to another also does not depend on the form of the trajectory, as well as the operation of a homogeneous field. On a closed trajectory, the operation of the electrostatic field is always zero.Fields possessing such a property called potential.Potential character, in particular, has an electrostatic field of point charge.
The work of the potential field can be expressed through a change in potential energy. Formula A \u003d - (W. n. 2 - W. nL. ) fair for any electrostatic field. But only in the case of a homogeneous field, the potential energy is expressed by the formula .
Potential.The potential charge energy in the electrostatic field is proportional to the charge. This is fair both for a homogeneous field and for inhomogeneous. Hence, the ratio of potential energy to the charge does not depend on the charge placed in the field.
This allows you to enter a new quantitative characteristic of the field - potential Φ. , effective charge placed in the field.
To determine the value of potential energy, as we know, you must select the zero level of its reference. When determining the potential of the field created by the charge system, it is assumed that the potential in an infinitely remote point of the field is zero.
The potential of the point of the electrostatic field is called the ratio of the potential energy of the charge placed at this point to this charge.
According to this definition, the potential is equal to:
Field tension E.- Vector magnitude. It represents power characteristic Fields that define the power acting on the charge q. at this point of the field. And the potential φ is a scalar, it energy characteristics of the field,it determines the potential charge energy q. at this point of the field.
If in an example with two charged plates as a point with zero potential, choose a point on a negatively charged plate, then according to the formulas, the potential of a homogeneous field is:
Potential difference. Like potential energy, the potential value at this point depends on the selection of the zero level to reflect the potential, i.e. from the point of choice, the potential of which is taken equal to zero. Change potentialit does not depend on the selection of the zero level of the reference of the potential.
Since potential energy, the work of the field forces is equal:
Here is the difference in potentials, i.e. the difference of potential values \u200b\u200bin the initial and endpoints of the trajectory.
Potential differences are also called voltage.
According to the formulas, the potential difference between two points turns out to be equal:
![]()
The potential difference (voltage) between the two points is equal to the function of the field when moving a positive charge from the starting point to the final value of this charge.
If the potential for the zero level of reference to the potential to accept the potential of an infinitely remote point of the field, then the potential at a given point is equal to the attitude of the electrostatic forces to move a positive charge from this point to infinity to this charging.
The difference unit of potentials. The unit of potential difference is set using the formula. In the international system of units, work is expressed in Joules, and the charge is in the coulons. Therefore, the potential difference between the two points is numerically equal to one, if when the charge is moving into1 CL from one point to another electric field makes work in1 J. This unit is called volt(IN); 1 B \u003d 1 J / 1 CL.
![]()