The concept of energy as physical quantity It is introduced to characterize the body's ability or body system to make work. As you know, exist different kinds Energy. Along with the kinetic energy already discussed above, which has a moving body, there are various types of potential energy: potential energy in the field of gravity, potential energy stretched or compressed spring or at all any elastic deformed body, etc.
Turning energy. The main property of energy consists in its ability to transform from one species to another in equivalent quantities. The known examples of such transformations are the transition of potential energy into the kinetic when the body falls from the height, the transition of kinetic energy into the potential when climbing the body thrown up, alternating mutual transformations of the kinetic and potential energies during pendulum oscillations. Each of you can lead a lot of other similar examples.
Potential energy Related to the interaction of bodies or parts of one body. For consistent administration of this concept, it is natural to consider the system of interacting bodies. The starting point here can serve as the theorem on the kinetic energy of the system, defined as the sum of the kinetic energies of the components of the particle system:
Work of domestic forces. As before, when the law of preserving the pulse of the body of the body was discussed, we will divide the power system acting on the bodies to external and internal. By analogy with the law, the impulse change one could expect that for the system of material points, the change in the kinetic energy of the system will be equal to the work of only the external forces acting on the system. But it is easy to see that it is not. By revising
changes in the full impulse of the system of the internal force pulses are mutually destroyed due to the third law of Newton. However, the work of the domestic forces will not be destroyed in pairs, since in the general case the particles to which these forces act can make different movements.
Indeed, when calculating the internal strength pulses, they multiplied to the same interaction time, and when calculating the work, these forces are multiplied by the movement of the corresponding bodies that may vary. For example, if two attractive particles will move towards each other, the internal forces of their interaction will make positive work and their amount will be different from zero.
Thus, the operation of the internal forces can lead to a change in the kinetic energy of the system. It is precisely due to this circumstance that the mechanical energy of the system of interacting bodies is not reduced only to the sum of their kinetic energies. The total mechanical energy of the system along with kinetic energy includes the potential energy of the interaction of the system particles. Full energy depends on the positions and velocities of particles, i.e. it is a function of the mechanical state of the system.
Potential energy. Along with the division of forces acting on the particles of the system, the external and internal, for the introduction of the concept of potential energy, you need to split all the forces into two groups on another basis.
In the first group, we will take strength, the work of which, when changing the mutual positions of the particles, does not depend on the method of changing the configuration of the system, that is, on which the trajectories and in which sequence of the system particles are moving from their initial positions in the final. Such forces will be called potential. Examples of potential forces can serve as forces, the Coulomb forces of the electrostatic interaction of charged particles, elastic strength. Relevant power fields Also called potential.
To the second group, we will take strength, the work of which depends on the form of the path. These forces are united under the name of unprofitable. The most characteristic example of non-optical forces is a sliding friction force, directed oppositely relative speed.
Work in a homogeneous field. Potential energy is quantitatively determined through the work of potential forces. Consider, for example, some body in a uniform field of gravity of the Earth, which, because of its large mass, we will be considered a fixed one. In a homogeneous field, the body acting on the body is the same everywhere, and therefore, as was shown in the previous paragraph,
her work when moving the body does not depend on the form of a trajectory connecting the initial and endpoint. The work of gravity when moving the body from position 1 to position 2 (Fig. 115) is determined only by the difference between heights in the initial and end positions:
Since the work does not depend on the form of the path, it can serve as the characteristic of the initial and endpoints, i.e. the characteristic of the power field itself.
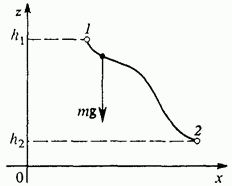
Fig. 115. The work of gravity when moving from position 1 to position 2 is equal to
We will take any point of the field (for example, the one on which the height in the formula for the beginning of the reference and will consider the work performed by the force of gravity when the particle is moved to this point from another arbitrary point p, which is at the height of this work, as follows from ( 2) is equal and called the potential energy of the particle at the point P:
In fact, this is the potential energy of the gravitational interaction of the body and the land that creates this field.
Work and potential energy. The work of gravity when moving the body from point 1 to point 2, given by formula (2), is equal to the difference in potential energies in the initial and endpoints of the path:
In an arbitrary potential field, where the module and direction of force depend on the position of the particle, the potential energy at some point P, as in a homogeneous field, is equal to the operation of the field force when the particle is moved from this point to the beginning of the reference, i.e. at a fixed point , the potential energy in which is accepted equal to zero. The choice of a point in which the potential energy is taken equal to zero is arbitrarily and is determined only by considerations of convenience. For example, in a homogeneous field of gravity of the Earth, the countdown of height and potential energy is convenient to move from the surface of the earth (sea level).
The noted ambiguity in determining the potential energy does not affect the results in the practical use of the concept of potential energy, since the physical meaning
it has only a change in potential energy, i.e. the difference of its values \u200b\u200bat two points of the field, through which the work of the field forces is expressed when the body is moved from one point to another.
Central field. We show the potential nature of the central field, in which the force depends only on the distance to the power center and is directed along the radius. Examples of central fields can serve as a field of planet or any body with a spherically symmetric distribution of masses, an electrostatic field point charge etc.
Let the body on which the central force acts on the radius from the power center O (Fig. 116) moves from point 1 to point 2 for some curve. We divide the whole way, into small areas so that the force within each site can be considered constant. Work work at such a plot
But as can be seen from fig. 116, there is a projection of the elementary movement to the direction of the radius-vector conducted from the Power Center: Thus, work in a separate section is equal to the work of force to change the distance to the power center. Summing up work in all areas, we are convinced that the work of the field forces when moving the body from point I to point 2 is equal to work on moving along the radius from point I to point 3 (Fig. 116). So, this work is determined only by the initial and finite distances of the body from the power center and does not depend on the form of the path, which also proves the potential nature of any central field.

Fig. 116. Work of the central field forces
Potential energy in the field of gravity. To obtain an explicit expression for the potential energy of the body at some point of the field, you need to calculate the work when moving the body from this point to another, the potential energy in which is taken equal to zero. We give expressions for potential energy in some important cases of central fields.
The potential energy of the gravitational interaction of point mass and M or bodies with a spherically symmetric distribution of masses whose centers are located at each other, is given by expression
![]()
Of course, we can talk about this energy and as about the potential energy of the body of the mass in the field of gravity created by the body of the mass M. In the expression (5), the potential energy is taken equal to zero with an infinitely large distance between the interacting bodies:
For the potential energy of the body of the mass in the field of land, it is convenient to modify formula (5) with regard to the relation (7) from § 23 and express the potential energy through the acceleration of the free drop in the earth's surface and the land radius
![]()
If the height of the body above the ground is small compared to the radius of the Earth, substituting in the form and using an approximate formula can be converted to formula (6) as follows:
The first term in the right side (7) can be omitted, as it is constantly, that is, it does not depend on the position of the body. Then instead (7) have
which coincides with the formula (3) obtained in the "flat" land approaching uniform field severity. We emphasize, however, in contrast to (6) or (7) in formula (8), the potential energy is counted from the surface of the Earth.
Tasks
1. Potential energy in the field of land. What is the potential energy of the body on the surface of the Earth and at an infinitely large distance from the ground, if we take it equal to zero in the center of the Earth?
Decision. To find the potential energy of the body on the surface of the Earth, provided that it is zero in the center of the Earth, it is necessary to calculate the work performed by the power of the body with a mental movement of the body from the surface of the Earth into its center. As was clarified earlier (see formula (10) § 23), acting on the body in the depths in the depths of the Earth, the force of gravity is proportional to its distance from the center of the Earth, if we consider the Earth with a homogeneous ball with the same everywhere density:
![]()
To calculate the work all the way from the surface of the Earth to its center, we divide into small sections, during which the strength can be considered constant. Work on a separate small area is depicted on the chart of the dependence of the force from the distance (Fig. 117) with an area of \u200b\u200ba narrow shaded strip. This work is positive, since the direction of gravity and movement coincide. Full work obviously
depicted with a triangle area with base and height
The value of potential energy on the surface of the earth is equal to the work given by the formula (9):
In order to find the value of potential energy at an infinitely large distance from the Earth, it should be noted that the difference in potential energies on infinity and on the surface of the earth is equal, in accordance with (6), and does not depend on where the zero of potential energy is selected. It is such a magnitude that needs to be added to the value (10) of potential energy on the surface to obtain the desired value at infinity:
2. Schedule of potential energy. Build a graph of the potential body of the body of the mass in the field of land, considering it a homogeneous ball.
Decision. We will take the value of potential energy in the center of the Earth equal to zero.

Fig. 117. To the calculation of potential energy
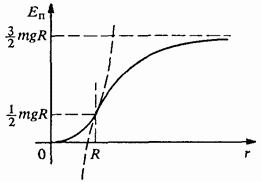
Fig. 118. Schedule of potential energy
For any inner point, located at the distance from the center of the Earth, the potential energy is calculated in the same way as in the previous task: as follows from fig. 117, it is equal to the triangle area with a base and a height in this way,
![]()
To construct a graph of potential energy at where, the force decreases inversely in proportion to the square of the distance (Fig. 117), the formula (6) should be used. But in accordance with the choice of the point of reference of potential energy to the value given to
moula (6), should be added a permanent amount so
The full schedule is shown on the plot from the center of the Earth to its surface, it is a segment of parabola (12), which is located at a minimum of which, with such a dependence, are sometimes called a "quadratic potential pit." On the plot from the surface of the Earth to infinity, the graph is a segment of hyperboles (13). These segments of parabola and hyperbolas smoothly, without a break, go into each other. The challenge of the graph corresponds to the fact that in the case of the attraction forces, the potential energy increases with increasing distance.
Elastic deformation energy. Potential forces also include forces arising from elastic deformation of tel. In accordance with the law of the throat, these forces are proportional to the deformation. Therefore, the potential energy of elastic deformation quadratically depends on the deformation. This becomes immediately clear if you consider that the dependence of the force from the displacement from the equilibrium position here is the same as in the gravity considered above, acting on the body inside a homogeneous massive ball. For example, with tension or compression on the elastic springs of stiffness to, when the current power is given to the expression
![]()
It is assumed here that in the equilibrium position the potential energy is zero.
Potential energy at each point of the power field has a definite value. Therefore, it can serve as the characteristic of this field. Thus, the power field can be described, setting either strength at each point, or the value of potential energy. These methods describing the potential power field are equivalent.
Communication of power and potential energy. We establish the connection of these two ways to describe, i.e. the total ratio between the force and change of potential energy. Consider moving the body between two close points of the field. The work of the forces of the field at the same time is equal to. On the other hand, this work is equal to the difference of potential energy values \u200b\u200bin the initial and endpoint points of the movement that is taken with the opposite sign a change in potential energy. therefore
![]()
The left side of this relationship can be written as a product of the projection of force on the direction of movement and the module of this movement from here
![]()
Projection potential power On an arbitrary direction, the ratio of potential energy changes taken with the opposite sign can be found at a small move along this direction to the movement module.
Equipotential surfaces. Both methods of description potential field You can compare visual geometric images - paintings silest lines or equipotential surfaces. The potential particle energy in the power field is the function of its coordinates. Equating a constant value, we obtain the surface equation, at all points of which the potential energy has the same value. These surfaces of equal values \u200b\u200bof potential energy, called Equipotential, give a visual picture of the power field.
Power at each point is directed perpendicular to passing through this point equipotential surface. It is easy to see with formula (15). In fact, choose moving along the surface of constant energy. Then, it is equal to zero projection of force on the surface so, for example, in a gravitational field created by the body of mass M with a spherically symmetric distribution of masses, the potential energy of the body of the mass is given by the expression of the surface of the constant energy of such a field are spheres whose centers coincide with the power center .
The force acting on the mass is perpendicular to the equipotential surface and is directed to the power center. The projection of this force on the radius conducted from the Power Center can be found from the expression (5) for potential energy using formula (15):
that when gives
![]()
The result obtained confirms the expression for potential energy (5) above without proof.
A visual representation of the surfaces of equal values \u200b\u200bof potential energy can be made on the embodiment of the crossed
terrain. Points of the earth's surface in one horizontal level correspond to the same values \u200b\u200bof the potential energy of the field of gravity. These points form continuous lines. On the topographic maps Such lines are called horizontals. Horizontally easily restore all the features of the relief: hills, depressions, saddles. On the steep slopes, the horizontal go thick, closer to each other than on the gentle. In this example, the lines are equal to the values \u200b\u200bof potential energy, and not the surface, since here we are talking about a power field, where the potential energy depends on the two coordinates (and not from three).
Explain the difference between potential and non-optical forces.
What is potential energy? What strength fields are called potential?
Get the expression (2) to work gravity in a homogeneous field of the Earth.
What is the associated ambiguity of potential energy and why does this ambiguity do not affect physical results?
Prove that in a potential power field, where work when moving the body between any two points does not depend on the form of the trajectory, work when moving the body for any closed pathway is zero.
Get the expression (6) for the potential energy of the body of the mass in the field of land. When is this formula?
How does the potential energy depend on the earth from the height above the surface? Consider cases when the height is small and when it is comparable with the radius of the Earth.
Specify on the graph of the dependence of potential energy from the distance (see Fig. 118) the area where the linear approximation is true (7).
The output of the formula for potential energy. In order to obtain a formula (5) for potential energy in the central field of gravity, it is necessary to calculate the operation of the field forces at a thought of moving the body of the mass from this point to an infinitely remote point. Work in accordance with formula (4) §§ 31 is expressed by the integral from the strength along the trajectory on which the body moves. Since this work does not depend on the form of the trajectory, it is possible to calculate the integral to move along the radius passing through the point you are interested in;
Denoting "action". You can call an energetic person who moves, creates a certain job, can create, act. Also, energy has vehicles created by people, live and dead nature. But it is in ordinary life. In addition, there is a strict science of physics that determined and denoted many types of energy - electrical, magnetic, atomic, etc. However, now it will be about the potential energy that cannot be considered in the detachment from the kinetic one.
Kinetic energy
This energy, according to the ideas of mechanics, have all the bodies that interact with each other. And in this case we are talking about the movement of tel.
Potential energy
A \u003d fs \u003d ft * h \u003d mgh, or Ep \u003d Mgh, where:
EP - Potential Body Energy,
m - body weight,
h - body height above the ground surface,
g - Acceleration of free fall.
Two types of potential energy
In potential energy, two types differ:
1. Energy with a mutual arrangement of tel. Such energy has a hanging stone. Interestingly, the potential energy has conventional firewood or coal. They contain not oxidized carbon, which can oxidize. If you say easier, burnt firewood can potentially heat the water.
2. Elderly elastic deformation. For example, here you can bring an elastic harness, compressed spring or system "bone-muscle-ligaments".
Potential I. kinetic energy We are interrelated. They can go into each other. For example, if you throw a stone up, when moving first, it possesses kinetic energy. When it reaches a certain point, then for a moment there is a cast and get potential energy, and then the gravity pulls it down and the kinetic energy will appear again.
Any body always has energy. If there is a movement, it is obvious: there is a speed or acceleration, which, multiplied by the mass, gives the desired result. However, in the case when the body is motionless, it, if neither paradoxical, can also be characterized as possessing energy.
So, it occurs when moving, potential - with the interaction of several tel. If everything is more and less obvious from the first, then often the force arising between two fixed objects remains beyond the understanding.
It is well known that the planet Earth affects all the bodies on its surface at the expense, that is, it attracts any item with a certain force. When moving the subject, changing its height, there is also a change in energy indicators. Immediately at the time of lifting the body has acceleration. However, at the highest point when the subject (even in a fraction of a second) is immobile, it has potential energy. The thing is that he is still pulling the field of the Earth, with which the body interacts.
Speaking otherwise, potential energy arises always due to the interaction of several objects forming the system, regardless of the size of the items themselves. At the same time, by default, one of them is represented by our planet.
Potential energy is a value depending on the mass of the subject and height on which it is raised. International designation - Latin letters EP. as follows:
Where m is a mass, G - acceleration H - height.
It is important to consider in more detail the elevation parameter, since it often becomes the reason for solving problems and understand the value of the value under consideration. The fact is that any vertical movement of the body has its own initial and end point. For the correct location of the potential energy of interaction bodies, it is important to know the initial height. If it is not specified, then its value is zero, that is, coincides with the surface of the Earth. In the case, if known as the initial point of reference and the final height, it is necessary to find the difference between them. The resulting number and will be the desired H.
It is also important to note that the potential energy of the system may have a negative value. Suppose we have already raised the body above the ground level, it became, it has a height that is called initial. When it sinks it, the formula will look like:
Obviously, H1 is greater than H2, therefore, the value will be negative, which will give the entire formula a minus sign.
It is curious that the potential energy is higher than the farther from the surface of the Earth the body is located. In order to better understand this fact, we think: the higher you need to raise the body above the ground, the thoroughly perfect work. The higher the value of the work of any strength, the fact that the energy is more invested. Potential energy, in other words, is the energy of the possibility.
Similarly, it is possible to measure the energy of the interaction of bodies when stretching the subject.
As part of the topic under consideration, it is necessary to separately discuss the interaction of the charged particle and electric field. In such a system, the potential energy of charge will be given. Consider this fact. For any charge, which is within the electrical field, the power of the same name operates. Moving the particle occurs due to the work produced by this force. Considering that the actual charge and (more precisely speaking, the body that created it) is a system, we also obtain the potential energy movement energy within the specified field. Since this type of energy is a special case, he was assigned the name of the electrostatic.
3.
H.minimum h. h.:
1) kinetic energy ball maximum
2) The potential energy of the spring is minimal
3) The potential energy of the ball interaction with the earth is maximum
Decision:
h., the ball changes the direction of his movement. It ceases to rise and begins to descend, so the speed of it at this point is zero, and therefore the kinetic energy is minimal. On the other hand, at this point, the ball is at the maximum height above the surface of the Earth, therefore, the potential energy of the interaction of the ball with the earth is maximum.
Note
It should be noted that the potential energy of the springs is minimal when the spring is not stretched. If you simply hang the cargo to the ceiling on the spring, the spring stretches, and when hesitations, the cargo will fluctuate around this new "stretched" equilibrium position. Therefore, if it turns out that h. exactly coincides with the long non-deformed spring, then at this point the spring will not stretch. Consequently, with this condition, item 2 will also be faithful.
4.
The cargo fluctuates on the spring suspended vertically to the ceiling, while the maximum distance from the ceiling to the cargo center is H, minimal h.. At the point removed from the ceiling at the distance h.:
1) kinetic energy ball maximum
2) kinetic energy ball minimal
3) the potential energy of the spring is maximum
4) The potential energy of the interaction of the ball with the earth is minimal
Decision:
At the point removed from the ceiling at the distance h., the ball changes the direction of his movement. It ceases to rise and begins to descend, so the speed of it at this point is zero, and therefore the kinetic energy is minimal. Approval 3 and 4 refer to the key position when it is removed from the ceiling for distance H.. At this point, the spring is stretched as much as possible, and the ball is on minimum distance from the earth.
5.
The load fluctuates on the spring suspended vertically to the ceiling, while the maximum distance from the ceiling to the center of cargo is equal H.minimum h.. The position of the equilibrium of the cargo is from the ceiling at a distance:
1) h.
2) H.
3) (H + H) / 2
4) (H-H) / 2
Decision:
The spring pendulum makes harmonic oscillations around its equilibrium position. Let be A. - amplitude of oscillations, and x. - The desired distance from the ceiling to the equilibrium position. Then
,
Where do you find that
6.
The ball varies on the spring, suspended vertically to the ceiling, while the maximum distance from the ceiling to the ball center is equal H.minimum h.. At the point removed from the ceiling at the distance H.Maximum:
1) kinetic energy ball
2) Potential Spring Energy
3) Potential Energy Energy Energy Energy
4) The sum of the kinetic energy of the ball and the interaction of the ball with the earth
Decision:
At the point removed from the ceiling at the distance H., the ball changes the direction of his movement. It ceases to descend and begins to rise, so the speed of it at this point is zero, and therefore the kinetic energy is minimal. At the same time, the ball is at the minimum distance from the Earth, therefore, the potential energy of interaction with the Earth is also minimal. Spring, on the contrary, it turns out in this position as stretched as much as possible. Thus, the statement 2 is true.
7.
The oscillatory movement of the body is set by the equation: ![]() ,
,
Where a \u003d 5 cm, b \u003d 3 s -1. What is the amplitude of oscillations?
Decision:
General view of the law of change over time the coordinates of the fluctuations in the body has
,
Where x MAX - amplitude of oscillations. Comparing with conclude that the amplitude of oscillations is equal x max \u003d a \u003d 5 cm
8. A cargo suspended on the spring of 400 N / m rigidity, performs free harmonic oscillations. What should be the rigidity of the spring so that the frequency of the oscillations of this cargo has increased by 2 times?
Answer: N / m.Decision:
The frequency of fluctuations of the spring pendulum is associated with the rigidity of the spring and the weight of the cargo by the ratio
Consequently, with a constant weight of the cargo to increase the frequency of oscillations, it is necessary to increase the rigidity of the spring 4 times. Thus, the rigidity of the spring must be equal to
9.
The figure shows the dependence of the amplitude of the established pendulum oscillations from the frequency of the forcing force (resonant curve). 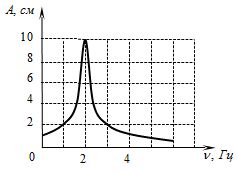
What is equal to the amplitude of the oscillations of this pendulum during resonance.
Decision:
The resonance is the phenomenon of a sharp increase in the amplitude of the forced oscillations when the frequency of the forcing force is approached to its own frequency of the pendulum. From the graph, it can be seen that the resonance occurs when the frequency of the forcing force in 1 Hz is found, the amplitude of the pendulum oscillations is 10 cm.
10.
A massive ball suspended on the spring makes harmonic oscillations along the vertical straight line. To increase the period of oscillations 2 times, enough bulb mass
1) increase by 4 times
2) reduce 4 times
3) increase by 2 times
4) reduce 2 times




