Gausa teorēma dažos gadījumos ļauj daudz vairāk atrast lauka intensitāti vienkārši līdzekļi nekā izmantojot formulu (5.3) lauka intensitātei punktu maksa un lauku superpozīcijas princips.
Demonstrēsim Gausa teorēmas iespējas, izmantojot vairākus piemērus, kas noderīgi turpmākajam. Pirms šo piemēru aplūkošanas mēs iepazīstinām ar virsmas un lineārā lādiņa blīvuma jēdzieniem.
Ja lādiņš ir koncentrēts lādiņu nesoša ķermeņa plānā virsmas slānī, lādiņa sadalījumu telpā var raksturot, izmantojot virsmas blīvumu o, ko nosaka izteiksme
Šeit - laukuma slānī esošais lādiņš. Ar to tiek domāts fiziski bezgalīgi mazs virsmas laukums.
Ja lādiņš ir sadalīts pa cilindriska korpusa tilpumu vai virsmu (vienmērīgi katrā sekcijā), izmanto lineāro lādiņa blīvumu
Fiziski bezgalīgi maza cilindra segmenta garums, lādiņš koncentrēts uz šo segmentu).
Bezgalīgas vienmērīgi uzlādētas plaknes lauks.
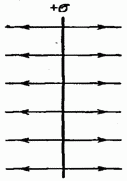
Lai virsmas lādiņa blīvums visos plaknes punktos ir vienāds un vienāds ar a; Noteiktības labad mēs pieņemam, ka lādiņš ir pozitīvs. No simetrijas apsvērumiem izriet, ka lauka intensitātei jebkurā punktā ir virziens, kas ir perpendikulārs plaknei. Patiešām, tā kā plakne ir bezgalīga un vienmērīgi uzlādēta, vektoram E nav iemesla novirzīties jebkurā virzienā no normālās uz plakni. Turklāt ir acīmredzams, ka punktos, kas ir simetriski attiecībā pret plakni, Lauka stiprums ir vienāds pēc lieluma un pretējs virzienā.
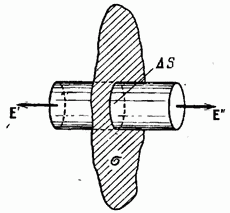
Garīgi iedomājieties cilindrisku virsmu ar ģeneratoriem, kas ir perpendikulāri plaknei, un lieluma bāzes atrodas simetriski attiecībā pret plakni (14.1. att.). Simetrijas dēļ Virsmai piemērosim Gausa teorēmu. Caur virsmas sānu daļu nebūs plūsmas, jo katrā punktā tā ir vienāda ar nulli. Pamatiem tas sakrīt ar E. Tāpēc kopējā plūsma caur virsmu ir vienāda ar Virsmas iekšpusē ir lādiņš a. Saskaņā ar Gausa teorēmu nosacījums
![]()
no kuriem
Mūsu rezultāts nav atkarīgs no cilindra garuma. Tas nozīmē, ka jebkurā attālumā no plaknes lauka stiprums ir vienāds. Spriegošanas līniju veids ir parādīts attēlā. 14.2. Negatīvi lādētai plaknei rezultāts būs tāds pats, tikai vektora E virziens un spriedzes līnijas mainīsies uz pretējo.
Ja ņemam galīgu izmēru plakni, piemēram, uzlādētu plānu plāksni, tad iepriekš iegūtais rezultāts būs derīgs tikai tiem punktiem, kuru attālums no plāksnes malas ievērojami pārsniedz attālumu no pašas plāksnes (14.3. att. šo punktu laukums ir apvilkts ar punktētu līkni).
Attālinoties no plaknes vai tuvojoties tās malām, lauks arvien vairāk atšķirsies no bezgalīgas lādētas plaknes lauka.
Lauka raksturu lielos attālumos ir viegli iedomāties, ja ņemam vērā, ka attālumos, kas ir daudz lielāki par plāksnes izmēru, tās radīto lauku var uzskatīt par punktveida lādiņa lauku.
Izmantojot Gausa teorēmu, dažos gadījumos ir viegli aprēķināt intensitāti elektriskais lauks ap lādētu ķermeni, ja dotajam lādiņu sadalījumam ir kaut kāda simetrija un var iepriekš uzminēt lauka vispārējo struktūru.
Piemērs ir plānsienu doba, viendabīgi uzlādēta gara rādiusa cilindra lauka aprēķināšanas problēma. R. Šai problēmai ir aksiālā simetrija. Simetrijas dēļ elektriskais lauks jābūt vērstam pa rādiusu. Tāpēc Gausa teorēmas pielietošanai vēlams izvēlēties slēgtu virsmu S kāda rādiusa koaksiāla cilindra formā r un garums l, abos galos slēgts (1.3.4. att.).
Plkst r ≥ R visa intensitātes vektora plūsma iet caur cilindra sānu virsmu, kuras laukums ir vienāds ar 2π rl, jo plūsma caur abām bāzēm ir nulle. Izmantojot Gausa teorēmu, tiek iegūts:
Šis rezultāts nav atkarīgs no rādiusa R uzlādēts cilindrs, tāpēc tas ir piemērojams arī gara vienmērīgi uzlādēta kvēldiega laukam.
Lai noteiktu lauka intensitāti uzlādēta cilindra iekšpusē, korpusam ir jākonstruē slēgta virsma r < R. Problēmas simetrijas dēļ lauka intensitātes vektora plūsmai caur Gausa cilindra sānu virsmu šajā gadījumā jābūt vienādai ar Φ = E 2π rl. Saskaņā ar Gausa teorēmu šī plūsma ir proporcionāla lādiņam, kas ieslodzīts slēgtās virsmas iekšpusē. Šī maksa ir nulle. No tā izriet, ka elektriskais lauks vienmērīgi uzlādēta garā dobā cilindrā ir nulle.
Potenciāls elektrostatiskais lauks. Teorēma par elektrostatiskā lauka cirkulāciju iekšā neatņemama forma. Elektrostatiskā lauka cirkulācijas teorēma diferenciālā formā. Vientuļa punktveida lādiņa potenciāls. Iespējamā atšķirība. ekvipotenciāla virsma. Iespējamā aditivitātes īpašība.
Elektrostatiskā lauka potenciāls. Konservatīvu spēka lauku var aprakstīt ne tikai ar vektora funkciju, bet līdzvērtīgu šī lauka aprakstu var iegūt, definējot piemērotu skalāro vērtību katrā tā punktā. Elektrostatiskajam laukam šis daudzums ir elektrostatiskā lauka potenciāls, kas definēts kā attiecība potenciālā enerģija testa maksa q līdz šī lādiņa vērtībai, j = W P / q, no kā izriet, ka potenciāls ir skaitliski vienāds ar potenciālo enerģiju, kas noteiktā lauka punktā piemīt vienībai pozitīvs lādiņš. Potenciāla mērvienība ir volts (1 V).
Potenciāls elektrostatiskais lauks - skalārs vienāds ar lādiņa potenciālās enerģijas attiecību laukā pret šo lādiņu:
Enerģētiskā īpašība lauki šajā brīdī. Potenciāls nav atkarīgs no šajā laukā ievietotā lādiņa lieluma.
Cirkulācijas teorēma
Ļaujiet lauku izveidot ar punktu maksu sistēmu. Aprēķināsim spriedzes integrāli pa slēgtu trajektoriju.
Šis apgalvojums ir cirkulācijas teorēmas būtība. Matemātikā šādu integrāli sauc par cirkulāciju.
Aprites jēdziens
Lai kādā telpas apgabalā ir vektoru lauks.
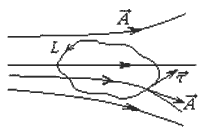
Šeit ir vienības vektora pieskares kontūrai noteiktā punktā, kas vērsta uz kontūras pozitīvo apiešanu.
Pastāv vienošanās, ka kontūras pārvietošanās pozitīvais virziens (virziens ) tiek izvēlēts tā, lai kontūras aptvertais laukums, šķērsojot, paliek kreisajā pusē.
Īsi atcerēsimies, kā var “konstruēt” līklīniju integrāli. Lai to izdarītu, jums ir jāizvēlas kontūras punkts, jāparāda tajā esošais vektors, tajā pašā punktā jāparāda pieskares vienības vektors, jāaprēķina skalārais reizinājums, jāsadala kontūra mazos elementos, jānorāda elementa garums. , aprēķināt preci; dariet to visiem kontūras elementiem; lai summētu rezultātus, novirzot kontūras garuma elementu uz nulli - pārejiet no summēšanas uz integrāciju.
Tāpat kā plūsma, cirkulācija ir vēl viena vektora lauka īpašību īpašība. Proti, cirkulācija raksturo vektora lauka virpuļošanas pakāpi.
Piemērs: ja turbīnu var ņemt par "mērītāju" šķidruma ātruma lauka cirkulācijai, tad, ja tā griežas, cirkulācija nav vienāda ar nulli.
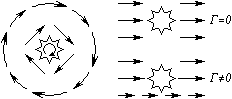
Aprite ir lauka neatņemama īpašība.
Rotora koncepcija
Lauks savā struktūrā var būt diezgan neviendabīgs. Tirāža nesniedz detalizētu lauka aprakstu. Tāpēc mēs sākam savilkt integrācijas kontūru līdz noteiktam punktam M(samazināt turbīnu). Tādā gadījumā cirkulācijai būs tendence uz nulli, bet arī kontūras aptvertajai zonai būs tendence uz nulli. Un to attiecība dod galīgu skaitli.
Turbīnu var orientēt telpā trīs neatkarīgos veidos. Līdz ar to šādā veidā var iegūt 3 neatkarīgus skaitļus, un trīs skaitļi ir vektors, tāpēc veidojas laukam raksturīgs vektors, ko sauc par rotoru.
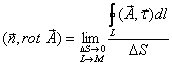
Rotors ir lokāls vai diferenciāls raksturlielums.
Tiek saukta virsma, kuras elektriskā lauka potenciālam visos punktos ir vienāda vērtība ekvipotenciāla virsma vai vienāda potenciāla virsma .
Elektrostatiskā lauka spēka līnijas vienmēr ir perpendikulāras ekvipotenciālu virsmām.
Punkta lādiņa Kulona lauka ekvipotenciālās virsmas ir koncentriskas sfēras. Uz att. 1.4.3 parāda dažu vienkāršu elektrostatisko lauku spēka līniju un ekvipotenciālu virsmu attēlus.
Kad viendabīgs lauks ekvipotenciālu virsmas ir paralēlu plakņu sistēma.
Ja testa maksa q apņēmusies maza nobīde līdzi lauka līnija no punkta (1) uz punktu (2), tad mēs varam rakstīt:
Šī attiecība skalārā formā izsaka attiecības starp lauka intensitāti un potenciālu. Šeit l ir koordināta, kas mērīta gar lauka līniju.
No lauka intensitātes superpozīcijas principa izveidots elektriskie lādiņi, potenciālu superpozīcijas princips ir šāds:
| φ = φ 1 + φ 2 + φ 3 + ... |
Potenciālu starpība (spriegums) starp diviem punktiem ir vienāds ar lauka darba attiecību, pārvietojot lādiņu no sākuma punkta uz beigu punktu uz šī lādiņa moduli:
U\u003d φ 1 - φ 2 \u003d -Δφ \u003d A/q,
A \u003d - (W p2 - W p1) \u003d -q (φ 2 - φ 1) \u003d -qΔφ
Potenciālo starpību mēra voltos (V = J / C)
Attiecība starp elektrostatiskā lauka stiprumu un potenciālu starpību:
E x = Δφ / Δ x
Elektrostatiskā lauka stiprums ir vērsts potenciāla samazināšanās virzienā.
Fizikā aditivitāte vērtības nozīmē, ka vērtība, kas saistīta ar sistēmu kopumā, ir vienāda ar vērtību summu, kas attiecas uz tās sastāvdaļām. Šos daudzumus sauc arī par plaša, Atšķirībā no intensīva(piemēram, temperatūra, blīvums utt.).
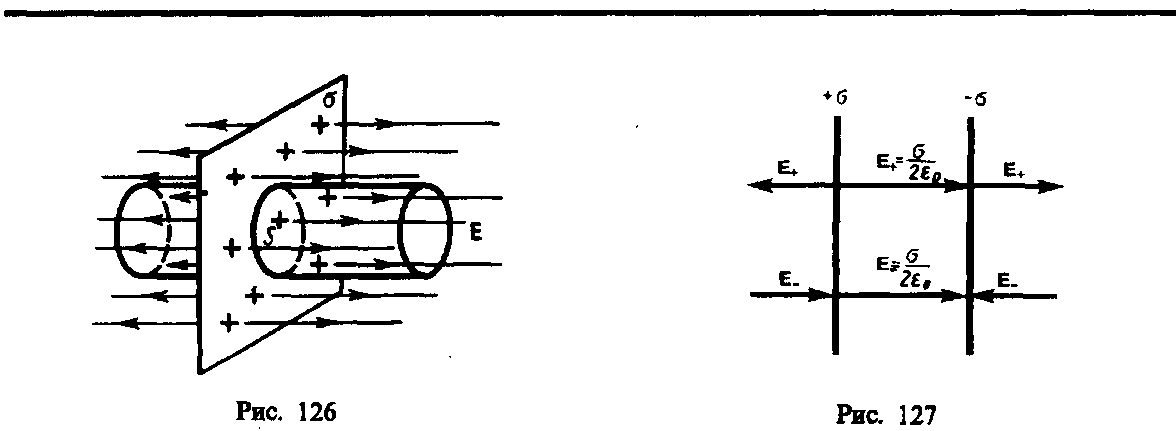
1. Vienmērīgi lādētas bezgalīgas plaknes lauks. bezgalīga plakne(126. att.) tiek uzlādēts ar konstanti virsmas blīvums +s(s = d Q/ d S- maksa par laukuma vienību). Spriegojuma līnijas ir perpendikulāras aplūkotajai plaknei un ir vērstas no tās abos virzienos. Domās konstruēsim cilindru kā slēgtu virsmu, kuras pamati ir paralēli lādētajai plaknei, un ass ir tai perpendikulāra. Tā kā cilindra ģeneratori ir paralēli spriegojuma līnijām (cosa = 0), tad spriegojuma vektora plūsma caur cilindra sānu virsmu ir vienāda ar nulli, un kopējā plūsma caur cilindru ir vienāda ar summu plūsmu caur tās pamatnēm (bāzu laukumi ir vienādi ar pamatni E n sakrīt ar E), t.i., vienāds ar 2 ES. Konstruētās cilindriskās virsmas iekšpusē ietvertais lādiņš ir vienāds ar s S. Saskaņā ar Gausa teorēmu (81.2), 2 ES= s S/ e 0 , kur
No formulas (82.1.) izriet, ka E nav atkarīgs no cilindra garuma, t.i., lauka stiprums jebkurā attālumā ir vienāds absolūtā vērtībā, citiem vārdiem sakot, vienmērīgi lādētas plaknes lauks viendabīgs.
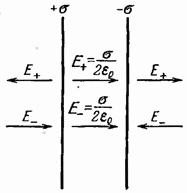
2. Divu bezgalīgu paralēlu pretēji lādētu plakņu lauks(127. att.). Lai plaknes ir uzlādētas ar vienmērīgi pretējiem lādiņiem ar virsmas blīvumu + s un –s. Mēs atrodam šādu plakņu lauku kā katras plaknes radīto lauku superpozīciju. Attēlā augšējās bultiņas atbilst laukam no pozitīvi lādētās plaknes, apakšējās bultiņas atbilst laukam no negatīvās plaknes. Pa kreisi un pa labi no plaknēm tiek atņemti lauki (spriegojuma līnijas ir vērstas viena pret otru), tāpēc šeit lauka stiprums E=0. Teritorijā starp lidmašīnām E= E + + E – (E+ un E- tiek noteiktas pēc formulas (82.1)), tāpēc iegūtais spriegums
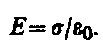 (82.2)
(82.2)
Tādējādi iegūto lauka intensitāti apgabalā starp plaknēm apraksta ar formulu (82.2), un ārpus tilpuma, ko ierobežo plaknes, tas ir vienāds ar nulli.
3. Vienmērīgi lādētas sfēriskas virsmas lauks. Sfēriskās virsmas rādiuss R ar kopējā maksa J vienmērīgi uzlādēts ar virsmas blīvumu +s. Tā kā lādiņš vienmērīgi sadalās pa virsmu, tā radītajam laukam ir sfēriska simetrija. Tāpēc spriegojuma līnijas ir vērstas radiāli (128. att.). Garīgi konstruēsim rādiusa sfēru r, kam ir kopīgs centrs ar uzlādētu sfēru. Ja r>R,ro viss lādiņš nokļūst virsmas iekšpusē J, kas rada aplūkojamo lauku, un, izmantojot Gausa teorēmu (81.2.), 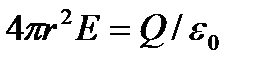 ,
kur
,
kur
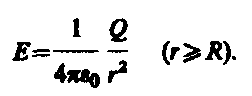 (82.3)
(82.3)
Plkst r>R lauks samazinās līdz ar attālumu r saskaņā ar to pašu likumu kā par punktu maksu. atkarības grafiks E no r attēlā parādīts. 129. Ja r"
4. Tilpumiski lādētas sfēras lauks. lodītes rādiuss R ar kopīgu lādiņu J vienmērīgi uzlādēts ar tilpuma blīvumu r(r = -lādiņš uz tilpuma vienību). Ņemot vērā apsvērumus
simetriju (skat. 3. nodaļu), var parādīt, ka lauka stiprumam ārpus lodes tiks iegūts tāds pats rezultāts kā iepriekšējā gadījumā (sk. (82.3)). Bumbiņas iekšpusē lauka stiprums būs atšķirīgs. Sfēras rādiuss r" 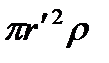 .
Tāpēc saskaņā ar Gausa teorēmu (81.2), . Atsaucoties uz
.
Tāpēc saskaņā ar Gausa teorēmu (81.2), . Atsaucoties uz 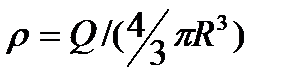 ,
mēs saņemam
,
mēs saņemam
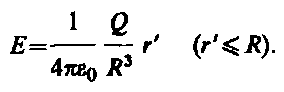 (82.4)
(82.4)
Tādējādi lauka intensitāti ārpus vienmērīgi uzlādētas lodes apraksta ar formulu (82.3), un tās iekšpusē lineāri mainās atkarībā no attāluma. r" saskaņā ar izteiksmi (82.4). atkarības grafiks E no r aplūkotajam gadījumam ir parādīts att. 130.
5. Vienmērīgi lādēta bezgalīga cilindra (vītnes) lauks. Bezgalīgs cilindra rādiuss R(131. att.) vienmērīgi uzlādēts ar lineārais blīvums t(t = - maksa par garuma vienību). No simetrijas apsvērumiem izriet, ka spriedzes līnijas tiks virzītas pa cilindra apļveida sekciju rādiusiem ar vienādu blīvumu visos virzienos attiecībā pret cilindra asi. Kā slēgtu virsmu mēs garīgi konstruējam koaksiālo cilindru ar uzlādētu rādiusu r un augstums l. Vektoru plūsma E caur koaksiālā cilindra galiem ir vienāds ar nulli (gali ir paralēli spriegojuma līnijām), un caur sānu virsmu ir vienāds ar 2 prlE. Pēc Gausa teorēmas (81.2), priekš r>R 2prlE = tl/e 0, no kurienes
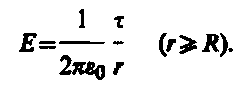 (82.5)
(82.5)
Ja r
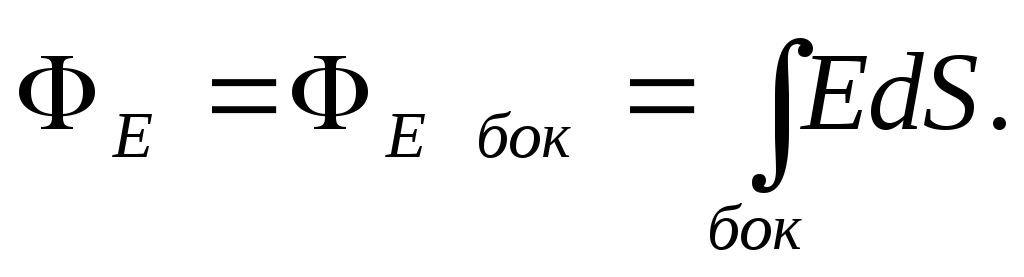
Acīmredzot tādā pašā attālumā r no nozīmes pavediena E būs tas pats, tātad 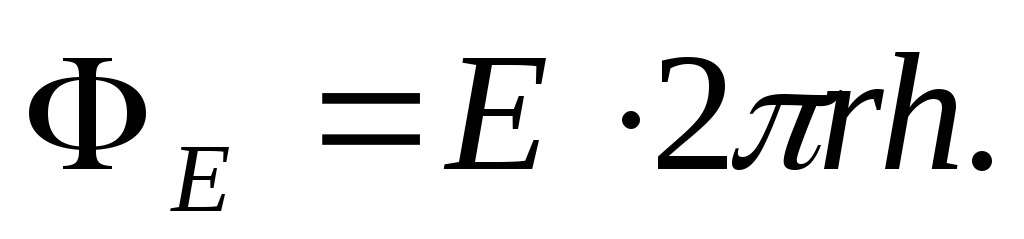 Saskaņā ar Gausa teorēmu
Saskaņā ar Gausa teorēmu
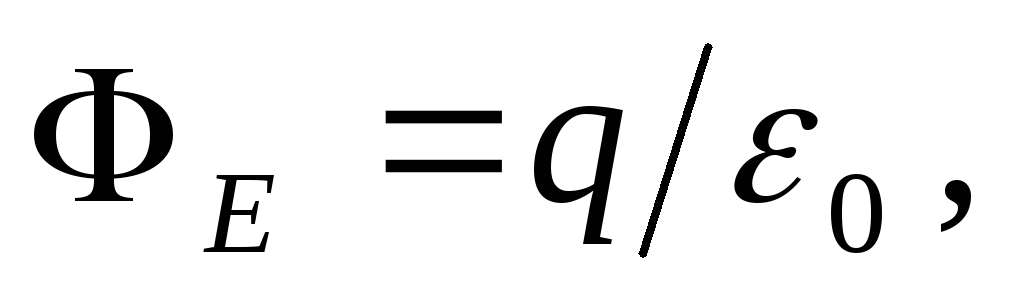
kur 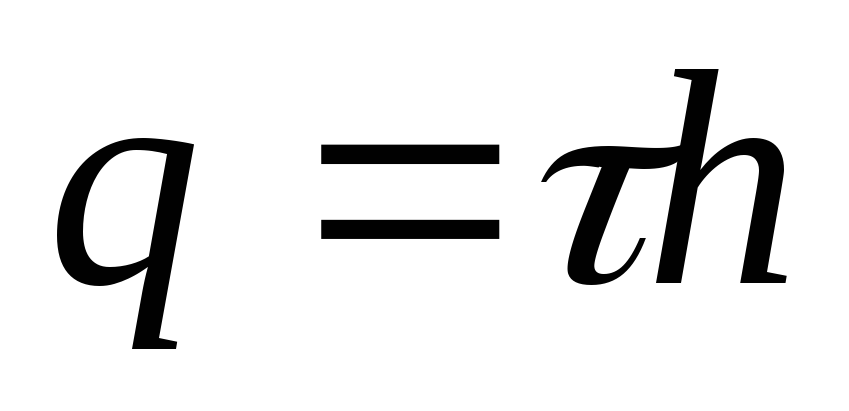 ir lādiņš, kas atrodas Gausa cilindra iekšpusē. Tad
ir lādiņš, kas atrodas Gausa cilindra iekšpusē. Tad
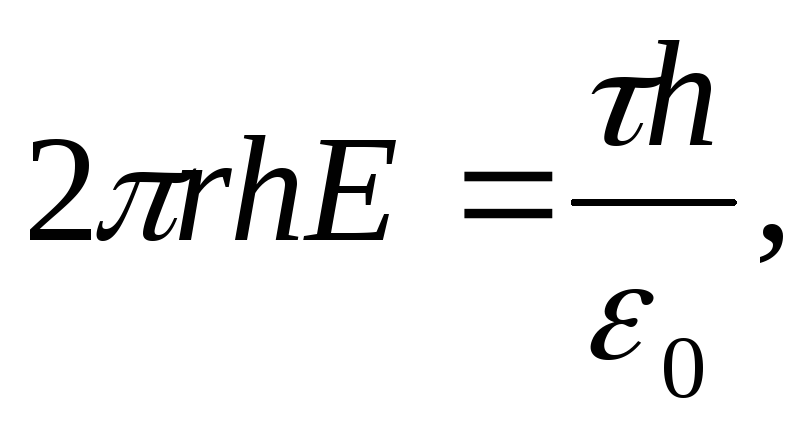
Un 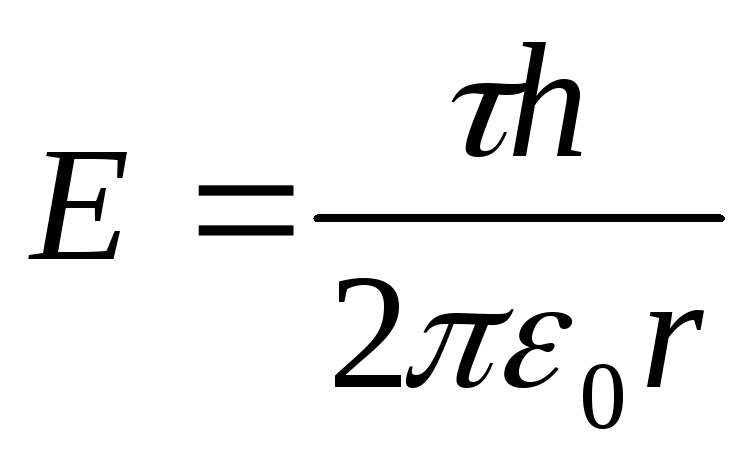 ir uzlādēta kvēldiega lauka stiprums attālumā r
no viņas.
ir uzlādēta kvēldiega lauka stiprums attālumā r
no viņas.
2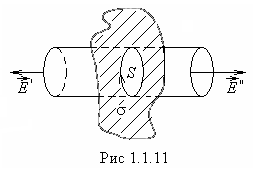 . Bezgalīgas viendabīgas lādētas plaknes lauks. Virsmas lādiņa blīvums
. Bezgalīgas viendabīgas lādētas plaknes lauks. Virsmas lādiņa blīvums  ir vienāda visos plaknes punktos
ir vienāda visos plaknes punktos  . Lauka stiprums ir perpendikulārs plaknei. Punktos, kas ir simetriski attiecībā pret plakni, lauka stiprums ir vienāds pēc lieluma un pretējs virzienā. Konstruēsim cilindrisku virsmu ar ģeneratoriem, kas ir perpendikulāri plaknei un pamatiem
. Lauka stiprums ir perpendikulārs plaknei. Punktos, kas ir simetriski attiecībā pret plakni, lauka stiprums ir vienāds pēc lieluma un pretējs virzienā. Konstruēsim cilindrisku virsmu ar ģeneratoriem, kas ir perpendikulāri plaknei un pamatiem  (1.1.11. att.). Simetrijas dēļ
(1.1.11. att.). Simetrijas dēļ  .
.
P 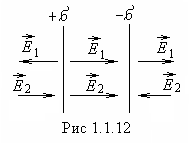 izplūde caur sānu virsmu ir vienāda ar nulli, jo vektors
izplūde caur sānu virsmu ir vienāda ar nulli, jo vektors  ir perpendikulāra šai virsmai, tātad kopējā plūsma caur cilindra virsmu ir
ir perpendikulāra šai virsmai, tātad kopējā plūsma caur cilindra virsmu ir 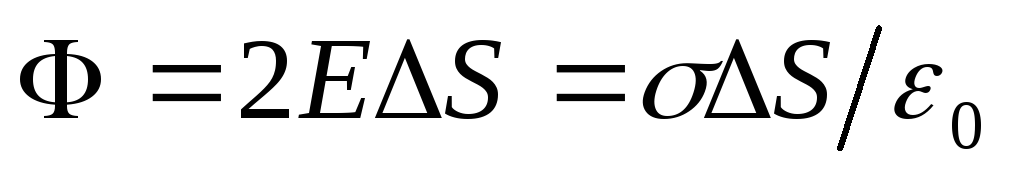 , Un
, Un 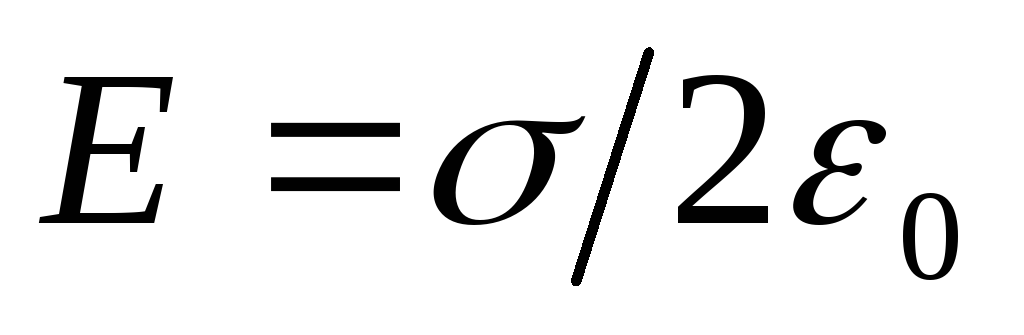 .
.
3. Aplūkosim elektrisko lauku, ko rada divas pretēji lādētas plaknes ar virsmas lādiņu blīvumu 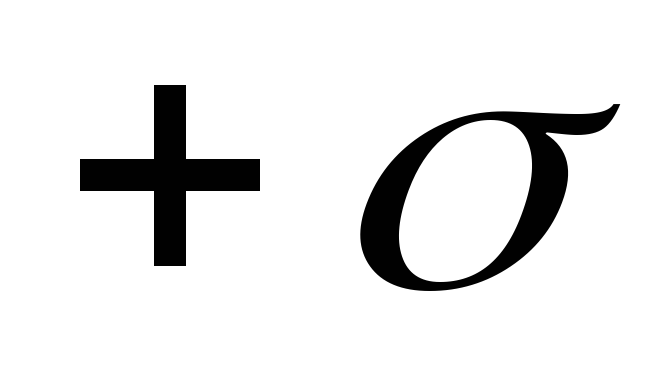 Un
Un 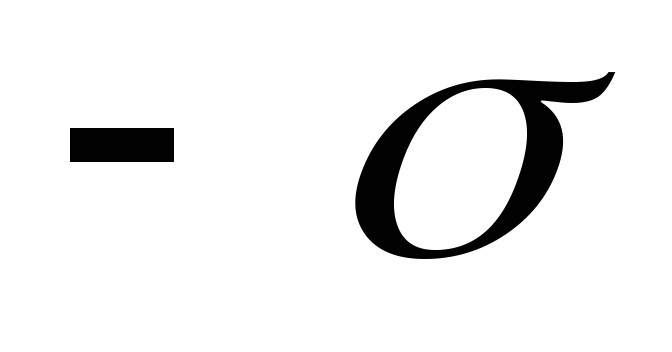 . Acīmredzot plakņu lauka intensitātes ir vērstas vienā virzienā (no pozitīvās plaknes uz negatīvo, 1.1.12. att.), un p.
. Acīmredzot plakņu lauka intensitātes ir vērstas vienā virzienā (no pozitīvās plaknes uz negatīvo, 1.1.12. att.), un p. 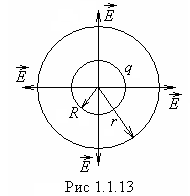 radušos spriedzi
radušos spriedzi 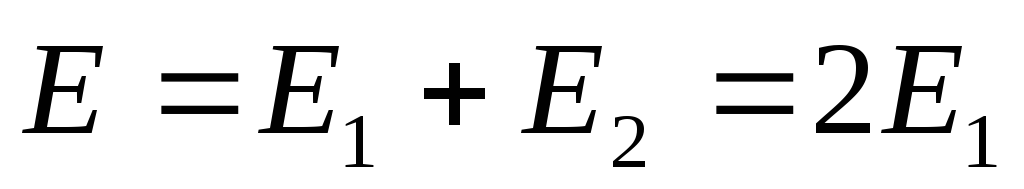 , kur
, kur 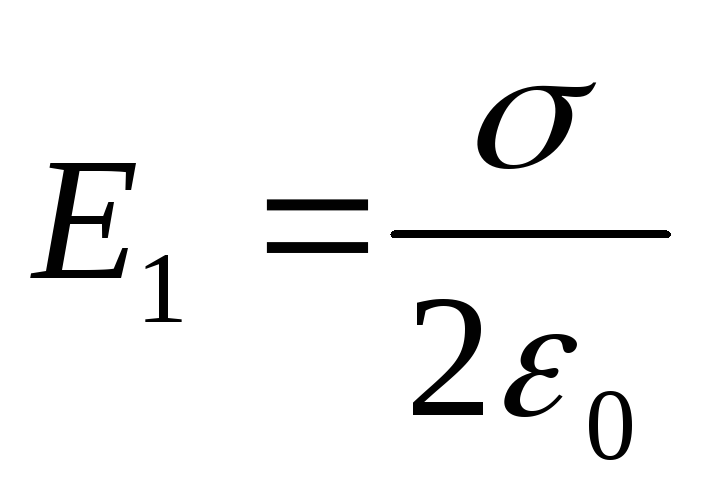 - vienas uzlādētas plaknes lauka stiprums. Beidzot saņemam
- vienas uzlādētas plaknes lauka stiprums. Beidzot saņemam
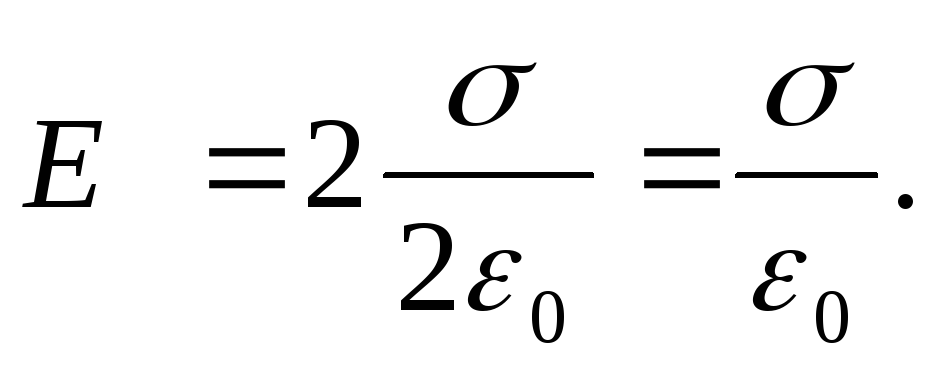
4. Aprēķināsim elektriskā lauka stiprumu, ko rada uzlādēta rādiusa sfēra R. sfēras lādiņš q, tā virsmas blīvums 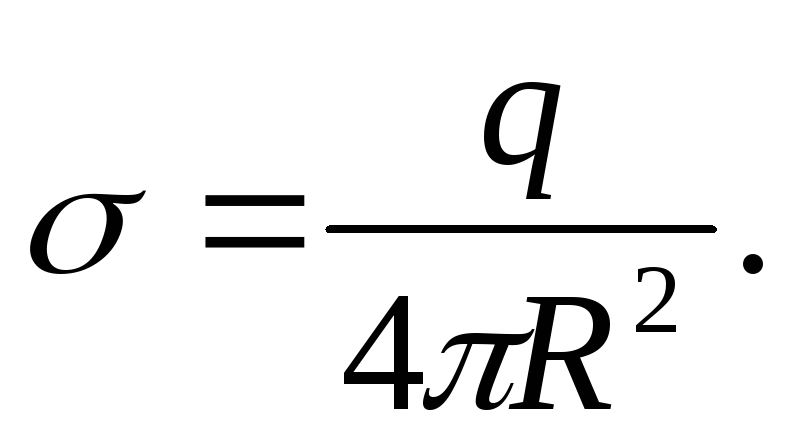 Lai noteiktu spriegumu, mēs izveidojam Gausa virsmu rādiusa sfēras formā r, kura centrs sakrīt ar lādētās sfēras centru (1.1.13. att.).
Lai noteiktu spriegumu, mēs izveidojam Gausa virsmu rādiusa sfēras formā r, kura centrs sakrīt ar lādētās sfēras centru (1.1.13. att.).
 Plkst r≤
R
Gausa virsmas iekšpusē nav lādiņu, jo viss lādiņš ir sadalīts pa sfēras virsmu. Saskaņā ar Gausa teorēmu
Plkst r≤
R
Gausa virsmas iekšpusē nav lādiņu, jo viss lādiņš ir sadalīts pa sfēras virsmu. Saskaņā ar Gausa teorēmu 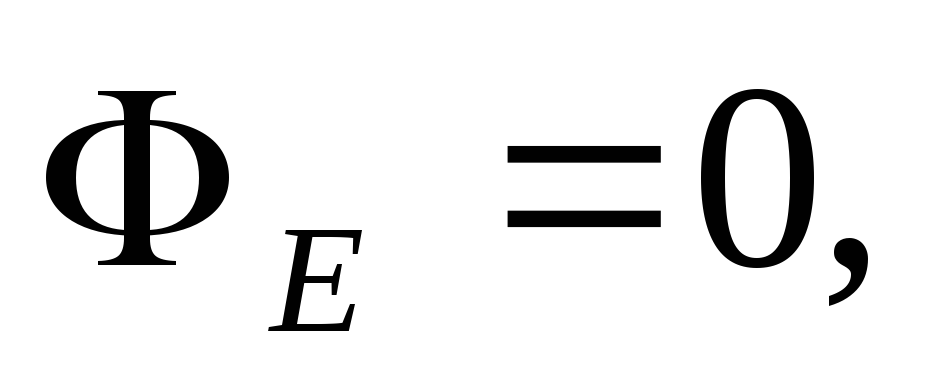 vai
vai 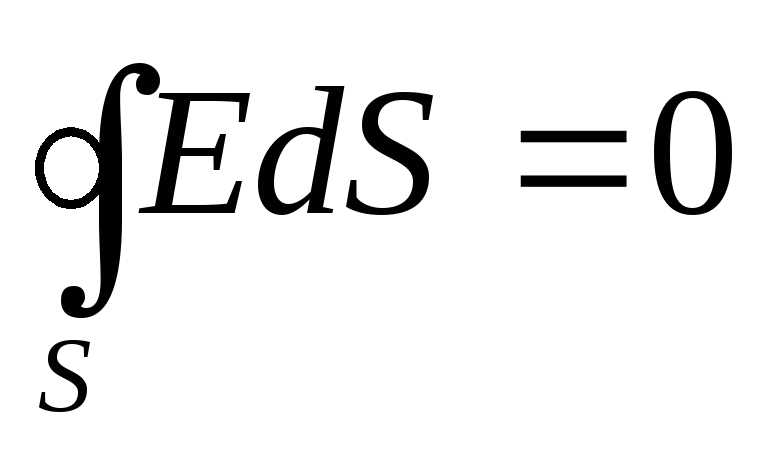 , tātad,
, tātad, 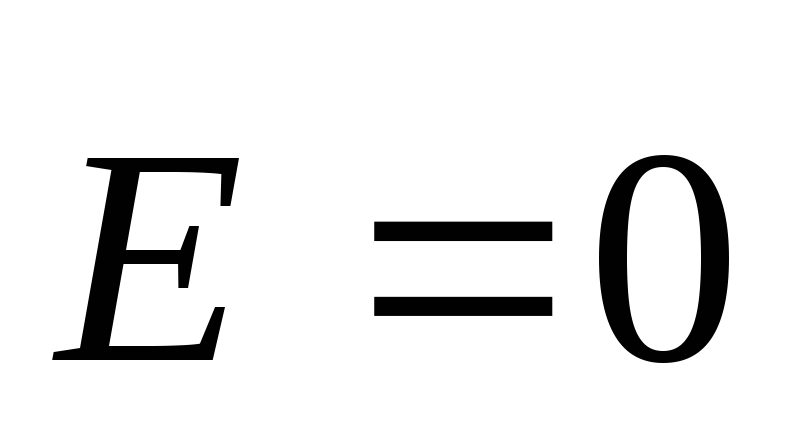 - elektriskā lauka stiprums uzlādētās sfēras iekšpusē ir vienāds ar nulli.
- elektriskā lauka stiprums uzlādētās sfēras iekšpusē ir vienāds ar nulli.
 Plkst
Plkst
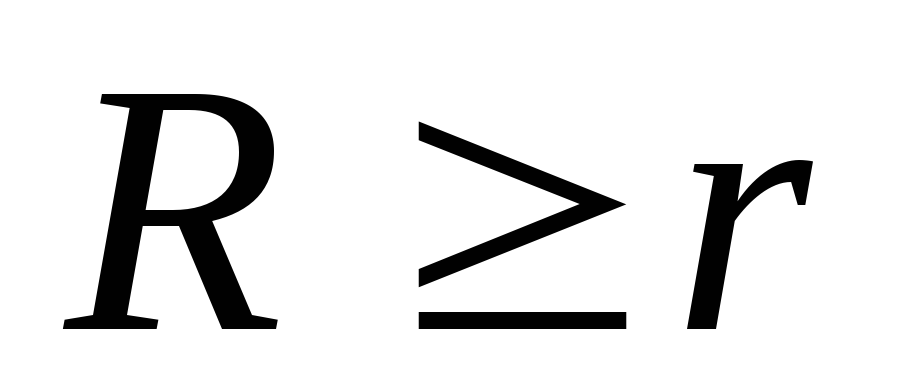 viss lādiņš nokļūst Gausa virsmas iekšpusē q sfēras. Lauka centrālās simetrijas dēļ intensitāte attālumā r no sfēras centra visur ir vienāds, un
viss lādiņš nokļūst Gausa virsmas iekšpusē q sfēras. Lauka centrālās simetrijas dēļ intensitāte attālumā r no sfēras centra visur ir vienāds, un 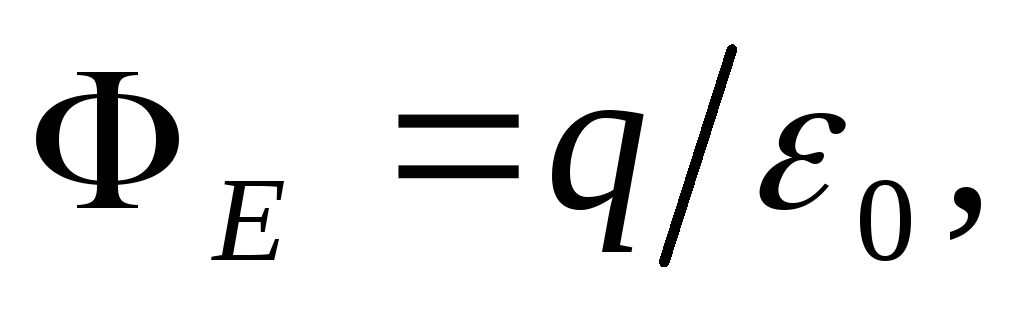 vai
vai 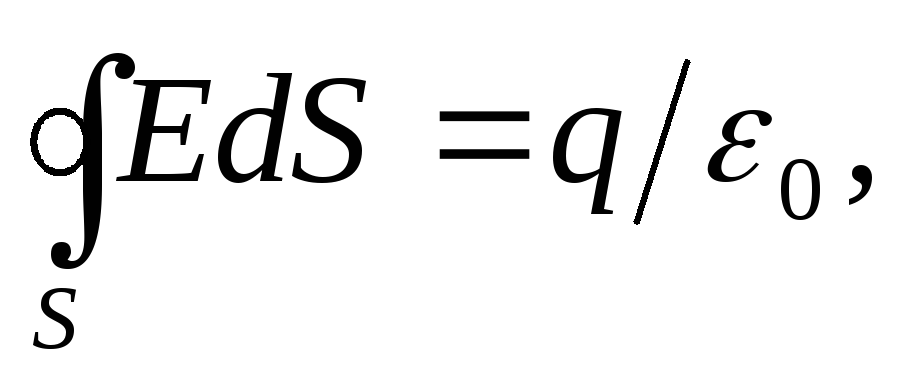 kurā
kurā 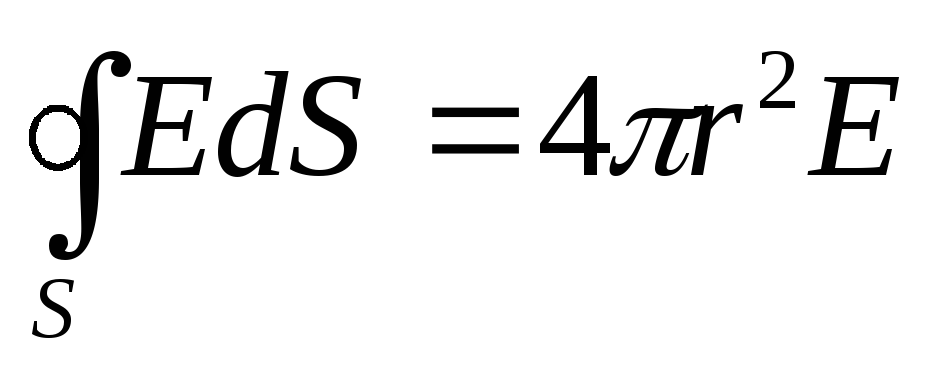 , tad un
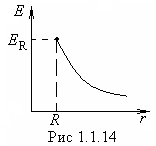
, tad un 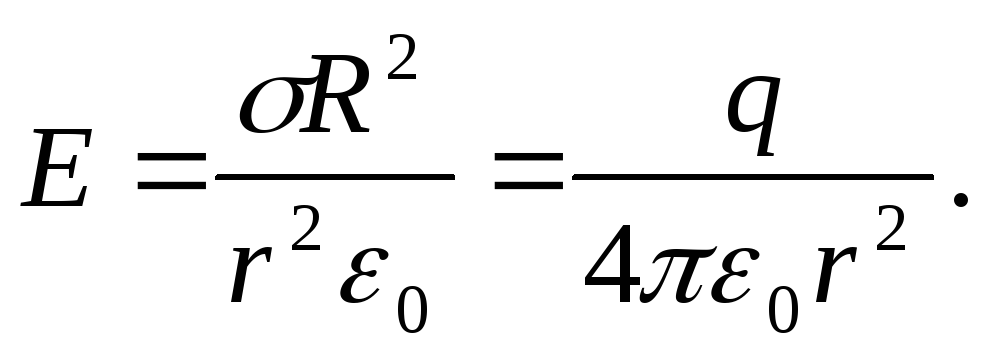 Ar izaugsmi r vērtības E proporcionāli samazināties
Ar izaugsmi r vērtības E proporcionāli samazināties 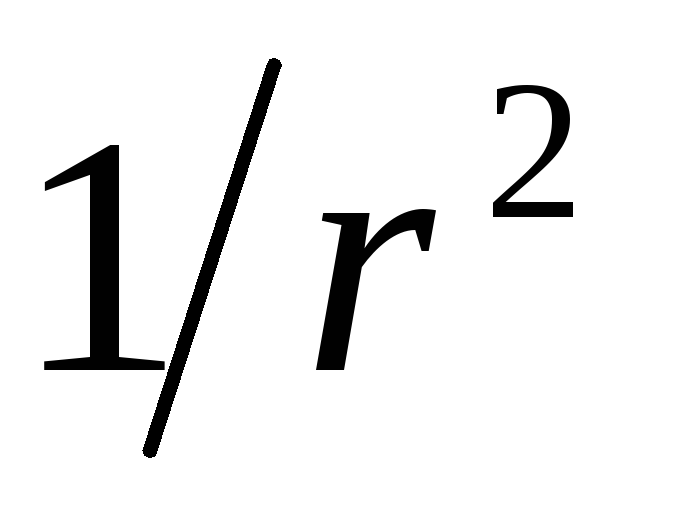 (1.1.14. att.). Uz sfēras virsmas spriedze piedzīvo lēcienu
(1.1.14. att.). Uz sfēras virsmas spriedze piedzīvo lēcienu 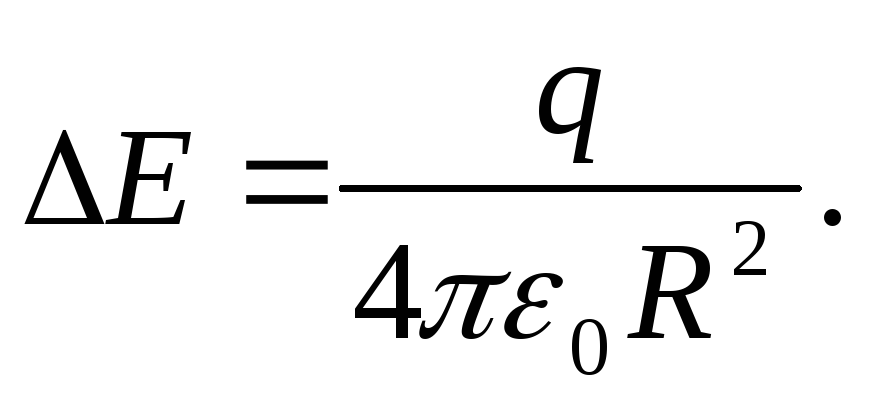
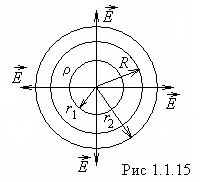
5. Aplūkosim elektrisko lauku, ko rada tilpuma lādēta rādiusa lode R. Bumbiņas tilpuma lādiņa blīvums ρ. Mēs izveidojam Gausa virsmu sfēras formā, kuras centrs sakrīt ar lodītes centru un rādiuss ir vienāds ar r (1.1.15. att.) .
Plkst 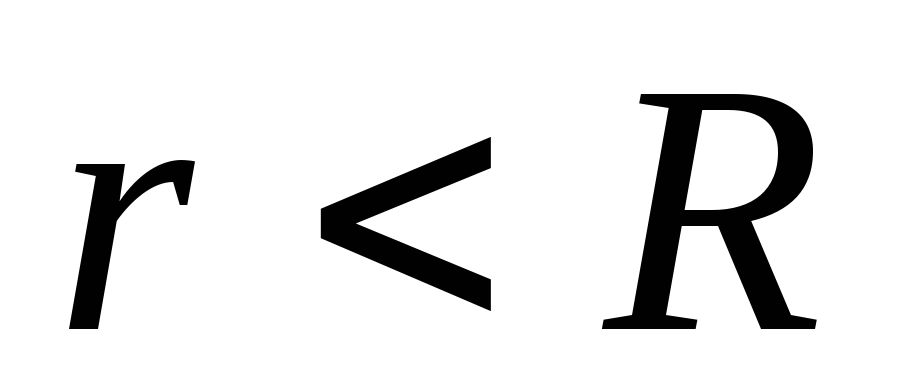 lādiņš nokļūst Gausa virsmā
lādiņš nokļūst Gausa virsmā
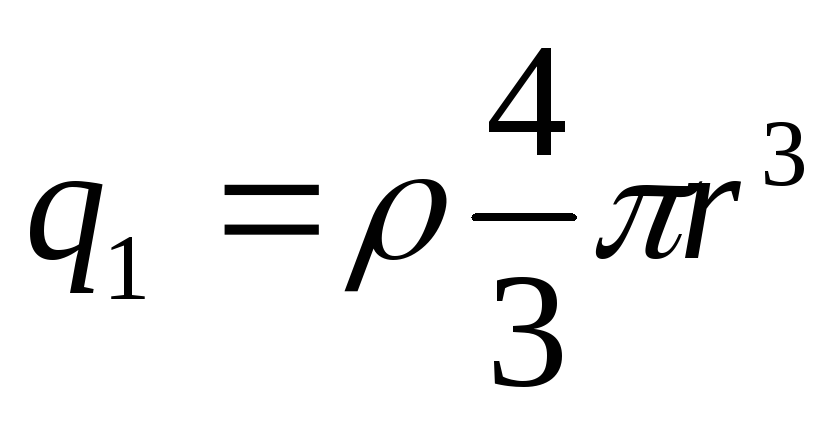 , tad pēc Gausa teorēmas
, tad pēc Gausa teorēmas 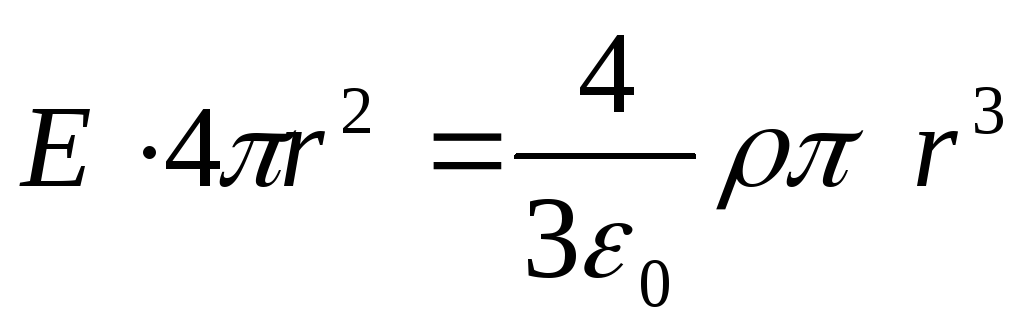 , Un
, Un 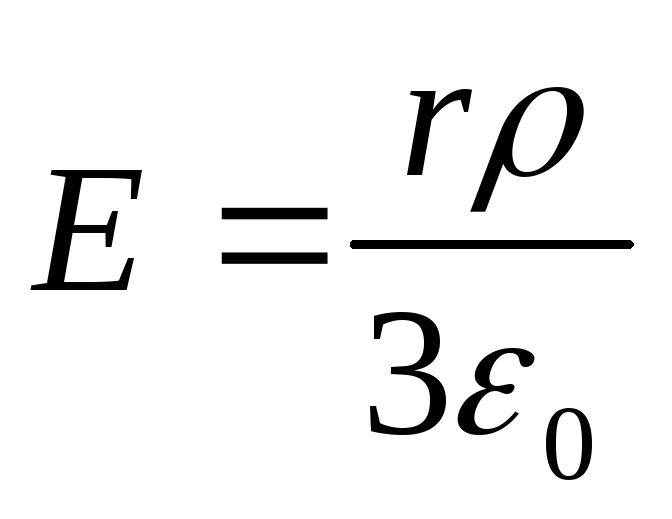 . Uz bumbas virsmas r=
R spriedze
. Uz bumbas virsmas r=
R spriedze 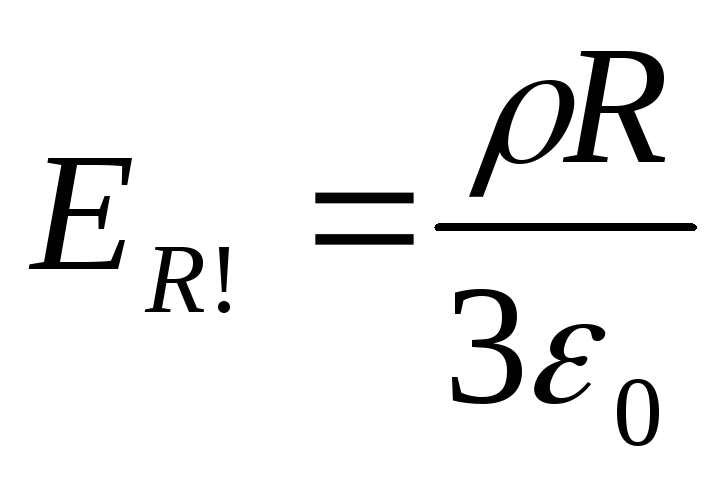 .
.
 Plkst
Plkst 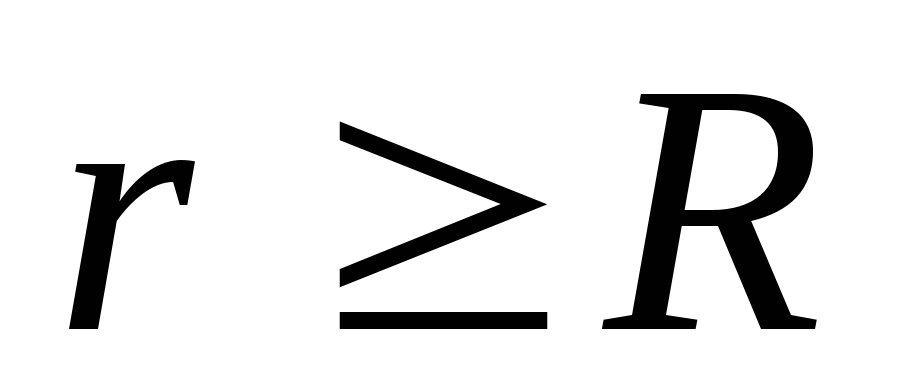 viss lādiņš nokļūst Gausa virsmas iekšpusē
viss lādiņš nokļūst Gausa virsmas iekšpusē 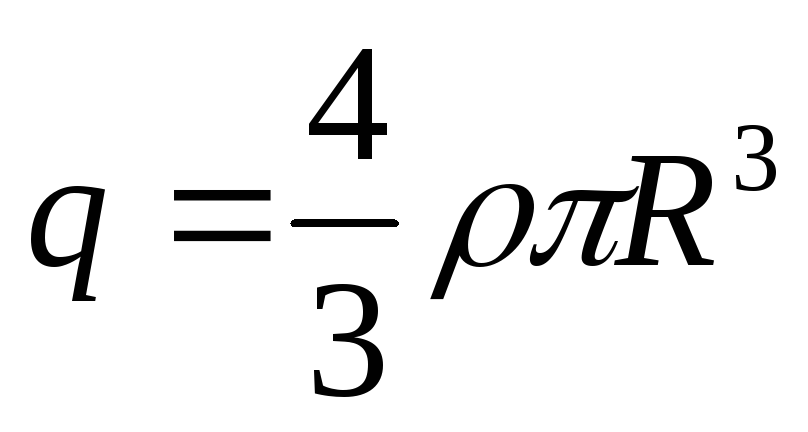 , Un
, Un 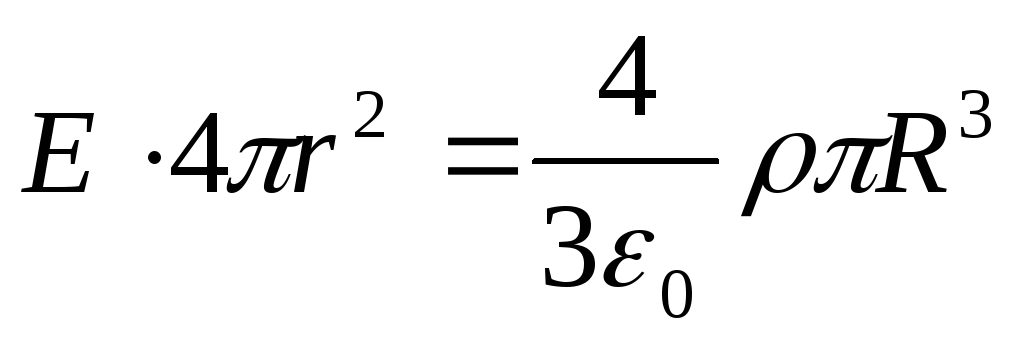 , tātad
, tātad 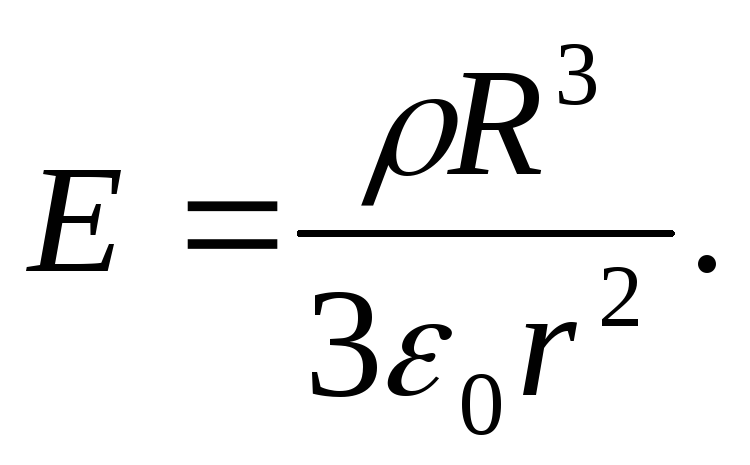 Uz sfēras virsmas
Uz sfēras virsmas 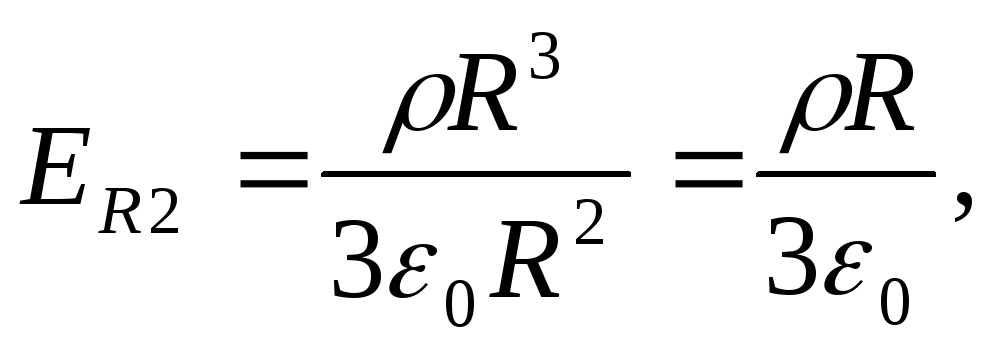 tie.
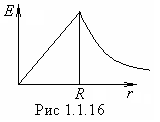
tie. ![]() un nav spriedzes lēciena. Atkarība
un nav spriedzes lēciena. Atkarība  parādīts 1.1.16. attēlā.
parādīts 1.1.16. attēlā.
4. lekcija
1.1.9. Elektrostatiskā lauka potenciālais raksturs. Lauka spēku darbs, pārvietojot lādiņus. Intensitātes vektora cirkulācija un rotors
Darbs, ko veic elektrostatiskā lauka spēki, pārvietojot lādiņu  segmentam
segmentam 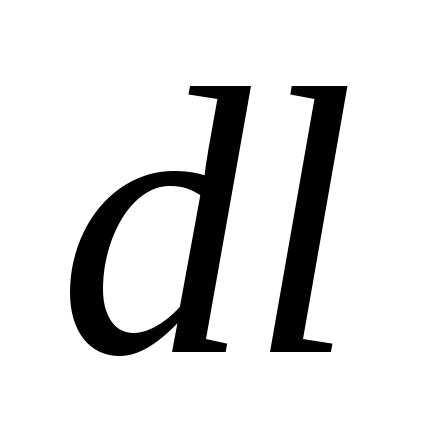 ir vienāds ar:
ir vienāds ar:
Vienības pozitīvā lādiņa pārvietošanas darbs ir skaitliski vienāds ar
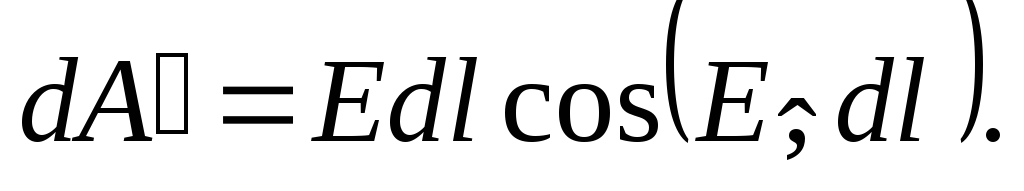
Darbs, kas veikts, pārvietojot vienības pozitīvo lādiņu pa ierobežotu ceļu 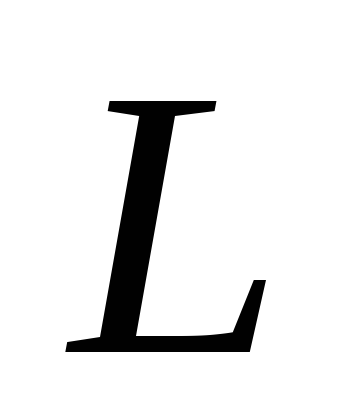 ir vienāds ar
ir vienāds ar
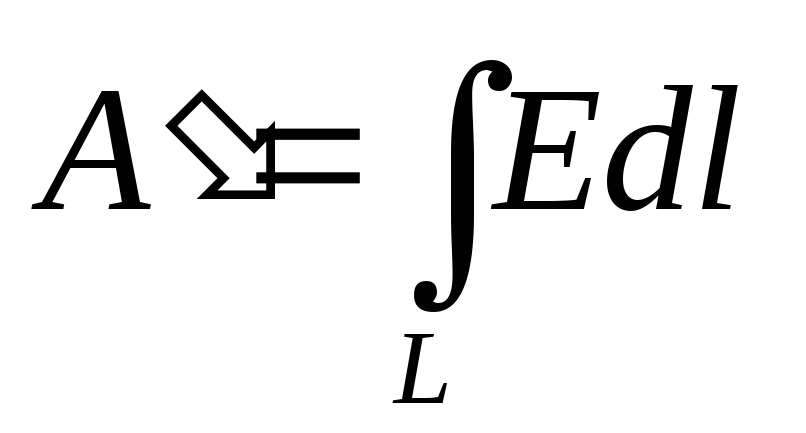 .
(1.1.2)
.
(1.1.2)
Šeit 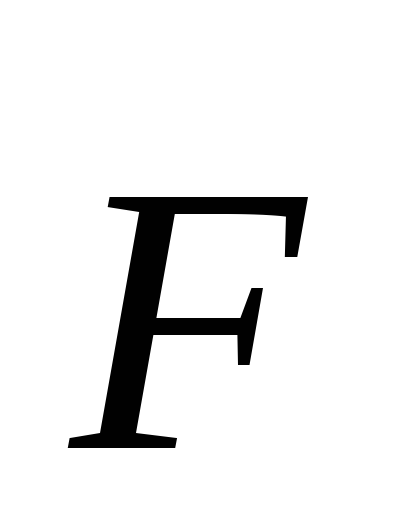 - Kulona spēks, kas ir centrālais spēks. No mehānikas ir zināms, ka centrālo spēku lauks ir konservatīvs. Līdz ar to elektrostatiskā lauka darbs lādiņa pārvietošanā nav atkarīgs no trajektorijas, bet tiek noteikts tikai pēc tā sākuma un beigu punktiem. Darbs uz slēgta ceļa ir vienāds ar nulli. Lauku ar šādām īpašībām sauc par potenciālu. Tad no (1.1.2) mums ir:
- Kulona spēks, kas ir centrālais spēks. No mehānikas ir zināms, ka centrālo spēku lauks ir konservatīvs. Līdz ar to elektrostatiskā lauka darbs lādiņa pārvietošanā nav atkarīgs no trajektorijas, bet tiek noteikts tikai pēc tā sākuma un beigu punktiem. Darbs uz slēgta ceļa ir vienāds ar nulli. Lauku ar šādām īpašībām sauc par potenciālu. Tad no (1.1.2) mums ir:
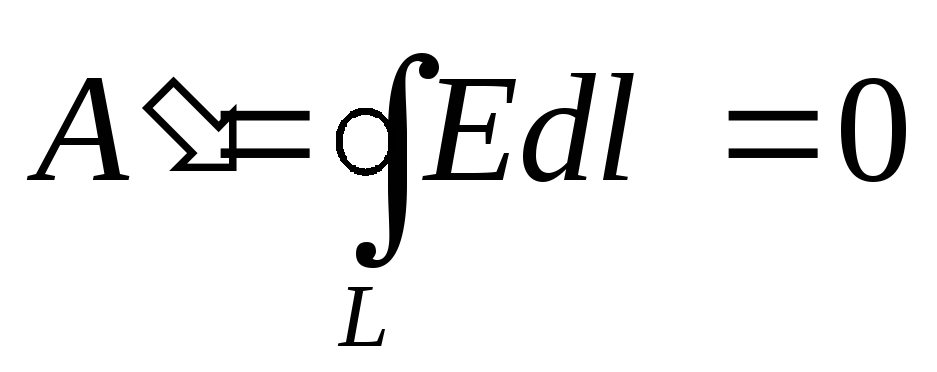 (1.1.3)
(1.1.3)
- vektoru cirkulācija  pa slēgtu ceļu ir nulle. Lauku ar šādām īpašībām sauc par potenciālu.
pa slēgtu ceļu ir nulle. Lauku ar šādām īpašībām sauc par potenciālu.
Pierādīsim elektrostatiskā lauka potenciālo raksturu.
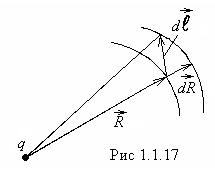 Vispirms apsveriet elektrisko spēku darbu elementāra punktveida lādiņa laukā
Vispirms apsveriet elektrisko spēku darbu elementāra punktveida lādiņa laukā  . Šo spēku darbs ar bezgalīgi mazu pārvietojumu
. Šo spēku darbs ar bezgalīgi mazu pārvietojumu  testa vienības pozitīvais lādiņš ir vienāds ar:
testa vienības pozitīvais lādiņš ir vienāds ar:
,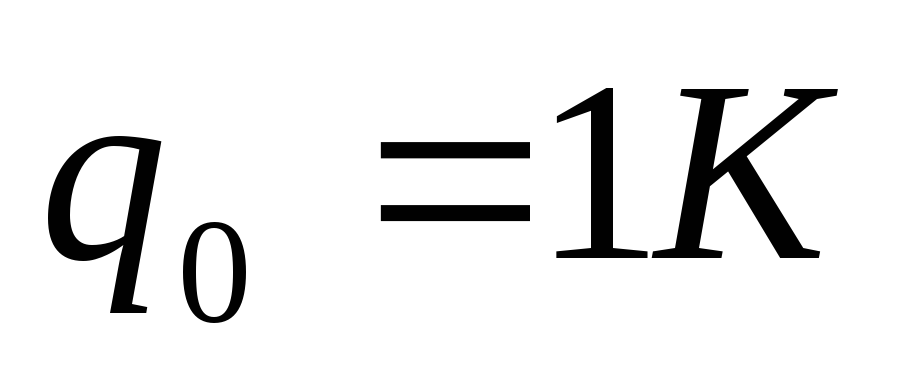
kur  - testa lādiņa nobīdes projekcija
- testa lādiņa nobīdes projekcija  uz rādiusa vektora
uz rādiusa vektora  no aizraujošā lauka lādiņa
no aizraujošā lauka lādiņa  . 1.1.17. attēlā redzams, ka
. 1.1.17. attēlā redzams, ka  ir rādiusa vektora skaitliskās vērtības pieaugums
ir rādiusa vektora skaitliskās vērtības pieaugums  , tas ir, testa uzlādes attāluma palielināšanās
, tas ir, testa uzlādes attāluma palielināšanās 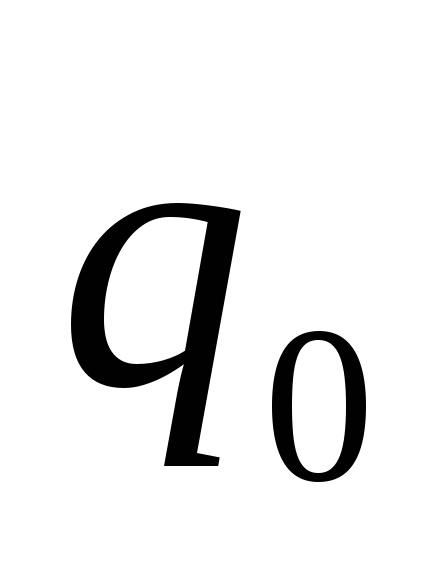 no maksas
no maksas  . Tāpēc strādājiet
. Tāpēc strādājiet  var attēlot kā skalārā punkta funkcijas kopējo diferenciāli
var attēlot kā skalārā punkta funkcijas kopējo diferenciāli 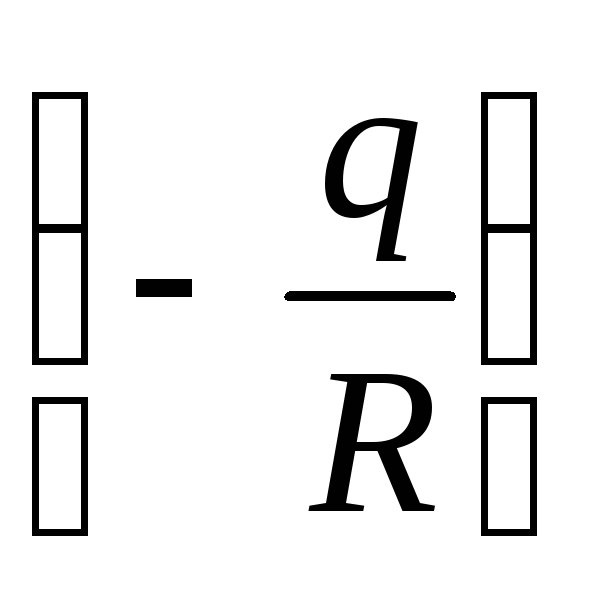 :
:
kur 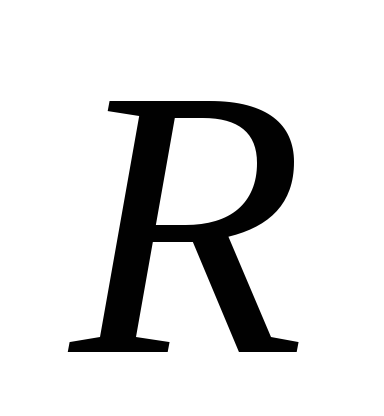 - rādiusa vektora skaitliskā vērtība
- rādiusa vektora skaitliskā vērtība  . Pēc tam darbs, lai pārvietotu vienību pozitīvu lādiņu no punkta
. Pēc tam darbs, lai pārvietotu vienību pozitīvu lādiņu no punkta 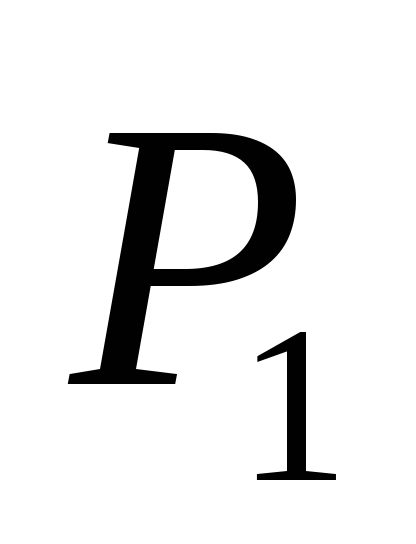 tieši tā
tieši tā 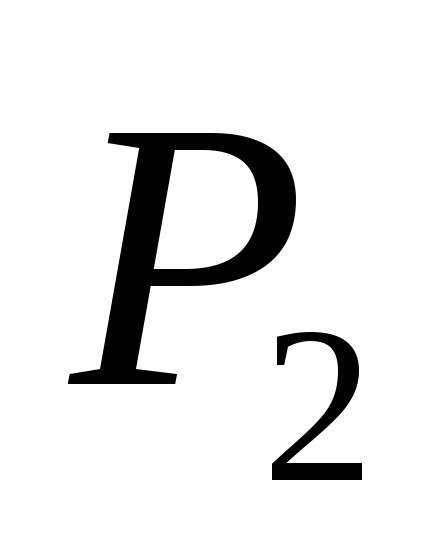 uz pēdējā ceļa
uz pēdējā ceļa 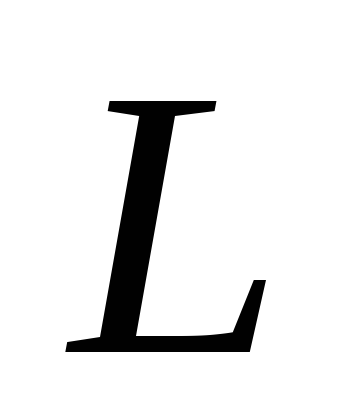 ir vienāds ar:
ir vienāds ar:
G 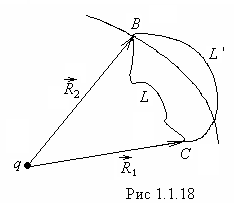 de
de  Un
Un 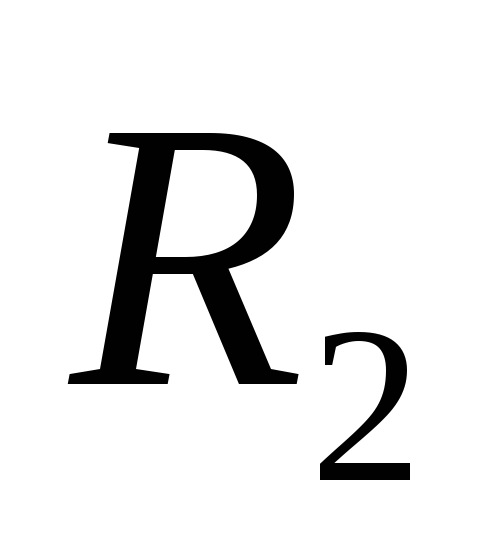 - ceļa sākuma un beigu punktu attālumi no lādiņa
- ceļa sākuma un beigu punktu attālumi no lādiņa  . Tādējādi elektrisko spēku darbs uz patvaļīga ceļa fiksētā laukā
. Tādējādi elektrisko spēku darbs uz patvaļīga ceļa fiksētā laukā
elementārais punktu lādiņš patiešām ir atkarīgs no šī ceļa sākuma un beigu punktu pozīcijām un nav atkarīgs no ceļa formas. Attēlā 1.1.18 darbs ceļā 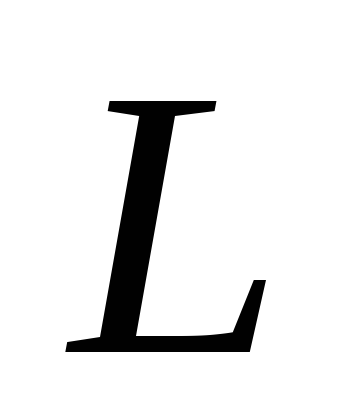 līdzvērtīgs darbam ceļā
līdzvērtīgs darbam ceļā 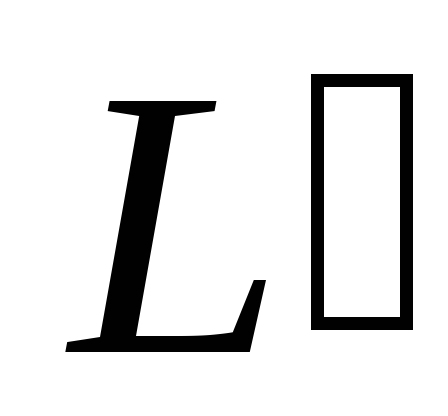 : takā veikts lieks darbs
: takā veikts lieks darbs 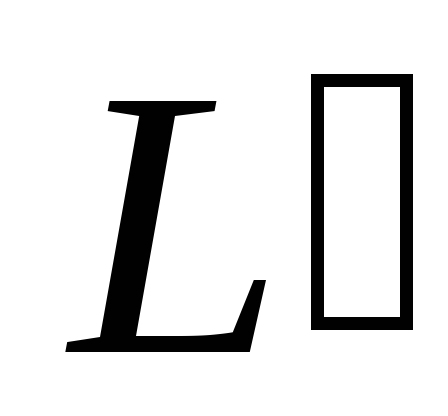 pārvietojot testa lādiņu ārpus rādiusa sfēras
pārvietojot testa lādiņu ārpus rādiusa sfēras 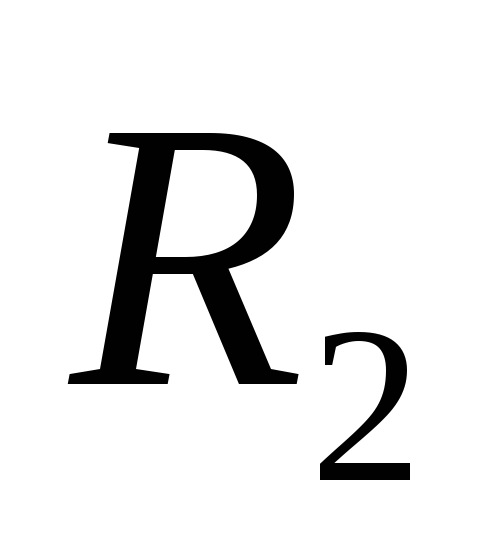 , tiek kompensēts ar negatīvo darbu, kas veikts turpmākās testa lādiņa pietuvināšanās lādiņam
, tiek kompensēts ar negatīvo darbu, kas veikts turpmākās testa lādiņa pietuvināšanās lādiņam  ceļojuma pēdējā posmā
ceļojuma pēdējā posmā 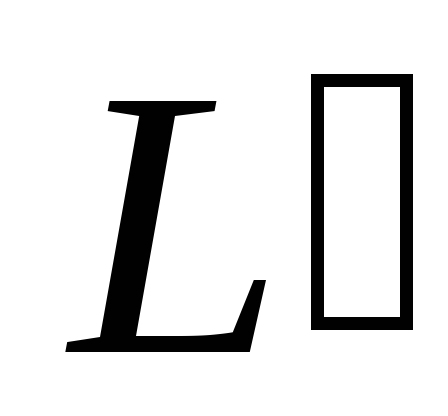 . Tādējādi fiksētā punkta lādiņa lauks ir potenciālais lauks.
. Tādējādi fiksētā punkta lādiņa lauks ir potenciālais lauks.
Acīmredzot potenciālo lauku summa ir arī potenciālais lauks (jo, ja spēku vārdu darbs nav atkarīgs no ceļa formas, tad no tā nav atkarīgs arī rezultāta darbs). Patvaļīgas lādiņu sistēmas lauku var uzskatīt par katra punktveida lādiņa lauku summu, tāpēc jebkurš elektrostatiskais lauks ir potenciāls lauks.
Pēc definīcijas projekcija  uz patvaļīgu lauka virzienu
uz patvaļīgu lauka virzienu 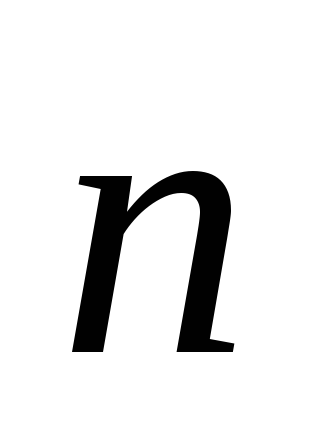 ir vienāds ar
ir vienāds ar
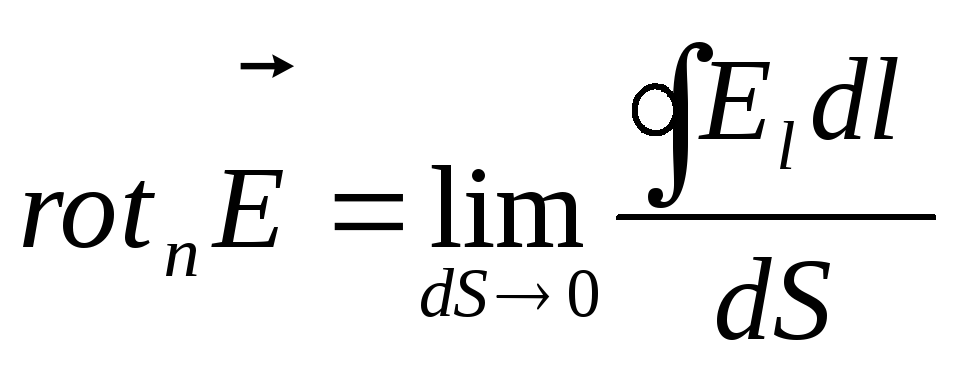 ,
,
kur  - bezgalīgi mazs laukums, kas iet caur punktu
- bezgalīgi mazs laukums, kas iet caur punktu 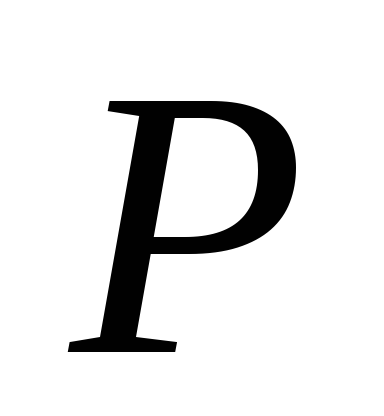 perpendikulāri vektoram
perpendikulāri vektoram 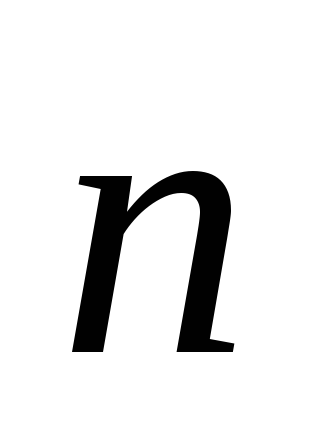 .
.
Kopš vektora cirkulācijas  slēgtā kontūrā ir vienāds ar
slēgtā kontūrā ir vienāds ar 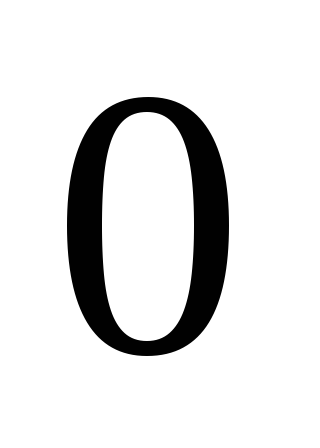 ,
,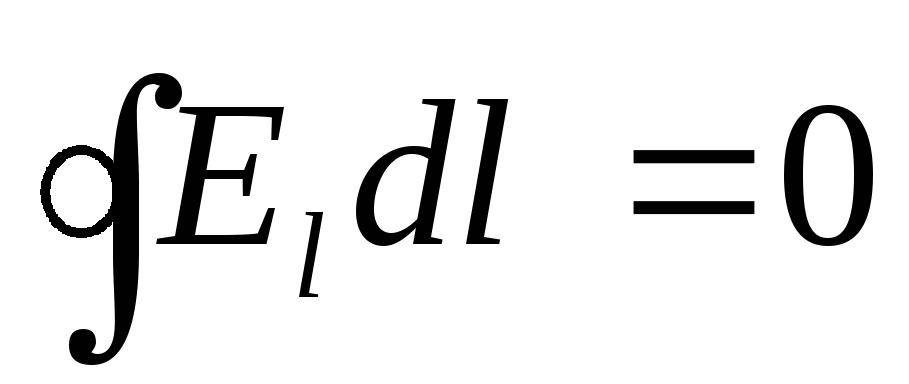 , tad
, tad
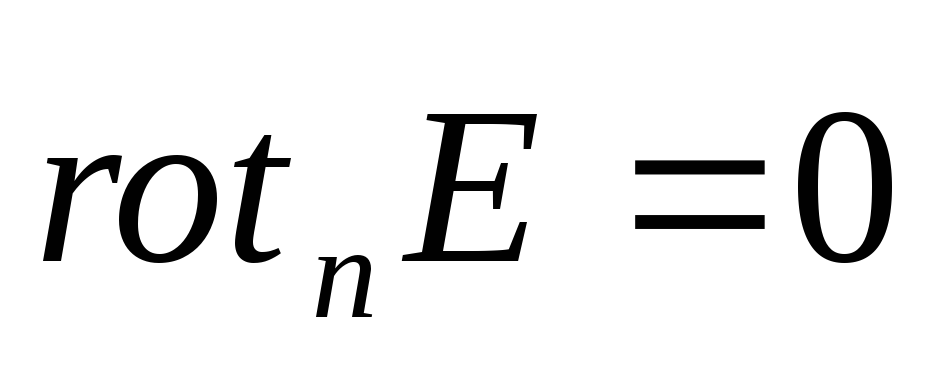 , vai
, vai 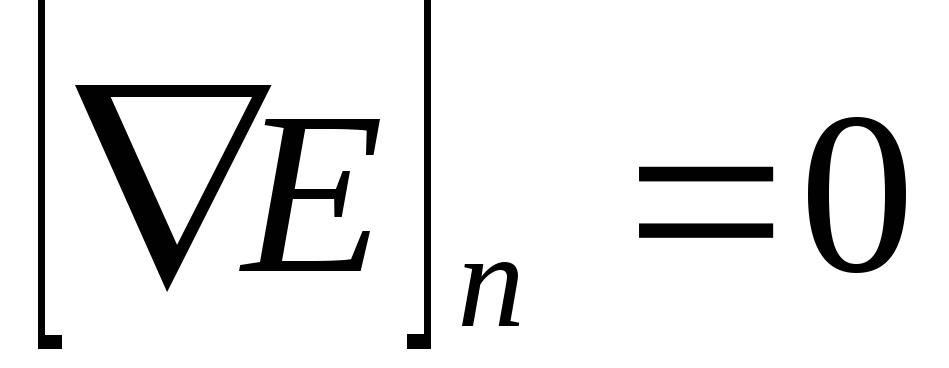 .
(1.1.4)
.
(1.1.4)
Kopš virziena 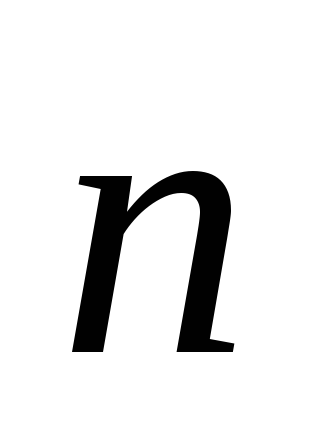 izvēlēts patvaļīgi, tad projekcija
izvēlēts patvaļīgi, tad projekcija  uz jebkuru virzienu ir 0, tātad no (1.1.4)
uz jebkuru virzienu ir 0, tātad no (1.1.4) 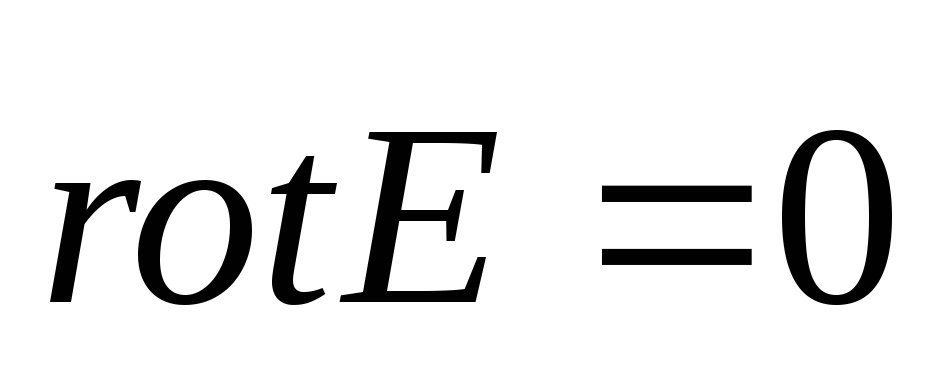 visos elektrostatiskā lauka punktos, tas ir, elektrostatiskais lauks ir
irrotējoša. Šo rezultātu var iegūt arī no Stoksa teorēmas. Izteiksmes (1.1.3.) un (1.1.4.) ir līdzvērtīgas.
visos elektrostatiskā lauka punktos, tas ir, elektrostatiskais lauks ir
irrotējoša. Šo rezultātu var iegūt arī no Stoksa teorēmas. Izteiksmes (1.1.3.) un (1.1.4.) ir līdzvērtīgas.




