लेकिन अ) सतही चार्ज घनत्व के साथ एक असीम रूप से चार्ज किए गए विमान का क्षेत्र। समरूपता के विचारों के लिए, यह स्पष्ट है कि फ़ील्ड को विमान के लिए लंबवत निर्देशित किया जाएगा - विमान से सकारात्मक शुल्क के लिए, जैसा कि चित्र में दिखाया गया है। 1.3, और नकारात्मक शुल्क के लिए विमान के लिए:
इसके अलावा, यह समरूपता विचारों से भी स्पष्ट है कि क्षेत्र सजातीय होगा। बनाने, लंबवत विमान और आधार के साथ एक बेलनाकार सतह की कल्पना करें डीएस।। अब हम सिलेंडर के माध्यम से प्रवाह पर विचार करते हैं। पक्ष की सतह के माध्यम से प्रवाह शून्य है और, इस प्रकार, सिलेंडर की सतह के माध्यम से पूरे प्रवाह को आधार के माध्यम से प्रवाह में कम किया जाएगा
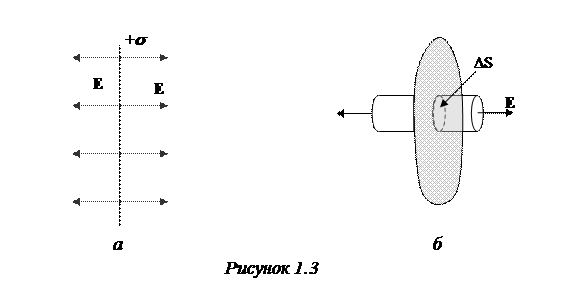
गॉसियन प्रमेय के आधार पर, यह प्रवाह चार्ज के बराबर है, जो सिलेंडर के अंदर विभाजित होता है ई 0.
जहां से यह इस प्रकार है
इस प्रकार, एक समान रूप से चार्ज किए गए विमान का क्षेत्र:
निर्देशित लंबवत विमान,
सजातीय है
विमान की दूरी पर निर्भर नहीं है।
बी) 2 का क्षेत्र बिल्कुल चार्ज विमानों । आरोपों की सतह घनत्व के साथ दो अलग-अलग चार्ज विमानों द्वारा गठित क्षेत्र एस, सुपरपोजिशन के सिद्धांत के आधार पर, आप अलग-अलग इन विमानों द्वारा बनाए गए क्षेत्रों को लागू करने के रूप में कल्पना कर सकते हैं। चूंकि विमानों के बीच अंतराल में इन क्षेत्रों को उसी तरह निर्देशित किया जाता है, इसलिए फ़ील्ड मान एक विमान द्वारा बनाए गए क्षेत्र के दोगुनी मान के बराबर होगा
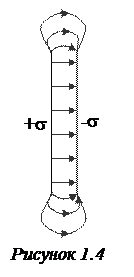विमानों द्वारा बंधे मात्रा के बाहर, फ़ील्ड अलग-अलग दिशाओं में निर्देशित होते हैं, और परिणामी क्षेत्र शून्य होता है। नतीजतन, दो समानांतर चार्ज विमानों द्वारा बनाई गई एक क्षेत्र:
सजातीय है
विमानों के बीच अंतराल में केंद्रित।
परिणामी निष्कर्ष लगभग फ्लैट कैपेसिटर्स के लिए मान्य हैं जिसके लिए विमानों (उन्हें प्लेट्स, या कैपेसिटर प्लेट्स कहा जाता है) प्लेटों (चित्र 1.4) के आयामों की तुलना में बहुत कम है।
में) एक अंतहीन चार्ज सिलेंडर का क्षेत्र।
एक अनंत त्रिज्या सिलेंडर होने दें आरसतही चार्ज घनत्व का आरोप लगाया एस (चित्र 1.5)। समरूपता विचारों के लिए, यह स्पष्ट है कि फ़ील्ड को सिलेंडर की धुरी के लिए लंबवत निर्देशित किया जाएगा, और इसका मूल्य सिलेंडर की दूरी पर निर्भर करेगा। मानसिक रूप से हमारे सिलेंडर को coaxially स्थित त्रिज्या सिलेंडर स्थित है आर और ऊंचाई एच और हम इस सिलेंडर तक सीमित सतह के माध्यम से तनाव वेक्टर की धारा की गणना करते हैं। समरूपता के विचारों के लिए, यह स्पष्ट है कि सिलेंडर के आधार के माध्यम से प्रवाह शून्य होगा। सिलेंडर की साइड सतह के माध्यम से प्रवाह के बराबर होगा ई (आर) 2 पीआरएच। गॉस प्रमेय के आधार पर, यह बराबर होगा 
। यहां एल एक रैखिक चार्ज घनत्व है।
. (1.29)
. (1.30)
अभिव्यक्ति (1.30) के लिए सत्य है आर\u003e आर।। गॉस प्रमेय के आधार पर खोखले सिलेंडर के अंदर, क्षेत्र शून्य है। यदि हम दो कोएक्सियल चार्ज सिलेंडर के बेलनाकार संधारित्र को समायोजित करते हैं, तो फ़ील्ड केवल सिलेंडरों के बीच शून्य से अलग होगा, और इसका मूल्य अभिव्यक्ति (1.30) द्वारा निर्धारित किया जाएगा। सुपरपोजिशन के सिद्धांत के आधार पर बाहरी सिलेंडर क्षेत्र के बाहर, 0 होगा। बेलनाकार संधारित्र (अंतिम लंबाई) का क्षेत्र बेलनाकार संधारित्र के क्षेत्र से अलग होगा अनंत लंबाई केवल किनारे पर।
डी) चार्ज गोलाकार सतह का क्षेत्र । चलो त्रिज्या क्षेत्र हो आरघनत्व के साथ भूतल प्रभार एस। समरूपता के विचारों के लिए, यह इस प्रकार है कि यह क्षेत्र केंद्रीय होगा। त्रिज्या के एक और केंद्रित क्षेत्र के हमारे क्षेत्र के चारों ओर आर। यदि एक आर\u003e आर।, फिर गॉसियन प्रमेय के आधार पर
,
. (1.31)
क्षेत्र के अंदर, क्षेत्र शून्य है। इस प्रकार, एक समान रूप से चार्ज किए गए क्षेत्र का क्षेत्र क्षेत्र के केंद्र में रखे बिंदु प्रभार के क्षेत्र के साथ मेल खाता है।
1. स्ट्रीम वेक्टर। यदि आप प्रवाह तरल पदार्थ के प्रवाह में डालते हैं, तो एक छोटा पारगम्य क्षेत्र डीएस।फिर तरल की मात्रा डीवीसमय की प्रति इकाई के माध्यम से बहने से द्रव प्रवाह दर की वेग के लिए सामान्य उत्पाद के बराबर होता है वी एन साइट की परिमाण से डीएस।,अर्थात डीवी=वी एन× डीएस।.
मूल्य वी एन यह पता लगाना आसान है कि क्या आप सामान्य (चित्र 12) के एक वेक्टर को निर्दिष्ट करते हैं। इस मामले में, और हम न केवल मंच के माध्यम से बहने वाले तरल पदार्थ की मात्रा को जानेंगे, बल्कि यह भी प्लेटफॉर्म के माध्यम से बहती है - सामान्य (सकारात्मक धारा) के अनुसार और सामान्य (नकारात्मक प्रवाह) के मुताबिक।
यदि साइट अंतिम आयाम है एस, और तरल पदार्थ की प्रवाह दर अलग-अलग बिंदुओं में अलग है, प्रति यूनिट बहने वाले तरल पदार्थ की मात्रा साइट पर एकीकरण द्वारा पाई जाती है। 
. (4.1)
इस अभिव्यक्ति में वेक्टर गति वी
उदाहरण के लिए, निरंतर बदलते वेक्टर द्वारा प्रतिस्थापित किया जा सकता है इ।
। इस मामले में, तरल पदार्थ की मात्रा के बजाय, हमें कुछ प्रकार की अमूर्त स्ट्रीम मिलती है एन वेक्टर इ।
अन्यथा स्ट्रीम वेक्टर तीव्रता.
1839 में, कार्ल गॉस ने दिखाया कि सममित इलेक्ट्रोस्टैटिक क्षेत्रों की गणना करते समय तनाव के वेक्टर को स्ट्रीम करने का विचार बहुत उपयोगी होता है।
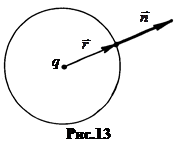
2. प्रमेय गॉस। रहने दो बिंदु प्रभार प्र एक मनमाना त्रिज्या के केंद्र में स्थित है आर। इस क्षेत्र की पूरी सतह पर वेक्टर के प्रवाह की गणना करें। वैक्टरों को ध्यान में रखते हुए और लेपित हैं, (चित्र .13)।
इस मामले में । (4.2)
स्ट्रीम वेक्टर इ।
क्षेत्र की सतह के माध्यम से अपने केंद्र में स्थित बिंदु प्रभार के आनुपातिक है प्र। अगर मैदान इ।
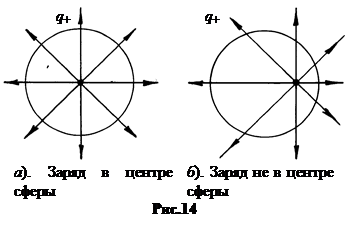
पावर लाइनों को चित्रित करें, फिर मूल्य इ। क्षेत्र की सतह के प्रत्येक बिंदु पर 1 मीटर 2 (चित्र 14 - ए) पर होने वाली रेखाओं की संख्या के बराबर होता है। और पूरी धारा एन वेक्टर इ।
सभी की संख्या के बराबर है स्लेस्ट लाइन्सआकर्षण प्र। के बाद से प्र क्षेत्र के अंदर और बाहर कोई अन्य शुल्क नहीं, तो सभी पंक्तियों को अनंत में जाना चाहिए। लेकिन इसका मतलब है कि क्षेत्र के अंदर किस स्थान पर लगाया गया था प्र, स्ट्रीम वेक्टर इ।
माध्यम की सतह के माध्यम से वही होगा (Fig.14-B)।
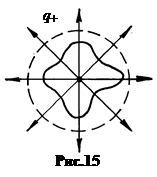स्ट्रीम वेक्टर इ।
मनमाने ढंग से आकार की बंद सतह के माध्यम से भी। यह इस तथ्य से देखा जा सकता है कि किसी भी बंद सतह को गोलाकार द्वारा कवर किया जा सकता है। चूंकि वेक्टर लाइनें इ।
ब्रेक नहीं है, तो क्या प्रवाह एन यह क्षेत्र के माध्यम से गुजरता है, यह किसी भी बंद सतह (चित्र 15) के माध्यम से है।
यदि बंद सतह के अंदर एक बिंदु चार्ज सिस्टम है क्यू I, फिर प्रवाह एन वेक्टर इ।
वैक्टर की धाराओं के योग के बराबर इ।
मैं। प्रत्येक शुल्क क्यू I: 
. (4.3)
तो, तनाव वेक्टर की पूर्ण धारा इ। एक बंद सतह आनुपातिक के माध्यम से कुल शुल्क सतह के अंदर। यह इलेक्ट्रोस्टैटिक प्रमेय गौससा.
यदि एक ज्ञात घनत्व समारोह के साथ, लगातार मात्रा में वितरित किया जाता है आरगॉस प्रमेय फॉर्म ले जाएगा: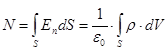 
. (4.4)
गॉसियन प्रमेय केवल तभी मान्य है जब बिंदु चार्ज क्षेत्र का तनाव वर्ग वर्ग के अनुपात में घटता है, जो कोलॉन के कानून द्वारा स्थापित किया जाता है।
उदाहरण 4.1। चार्ज किए गए क्षेत्र का क्षेत्र। हम मानते हैं कि चार्ज सतह घनत्व के साथ क्षेत्र में समान रूप से वितरित किया जाता है एस। क्षेत्र का त्रिज्या आर। अलग-अलग स्थान के दो क्षेत्रों पर विचार करें - क्षेत्र के अंदर और बाहर।
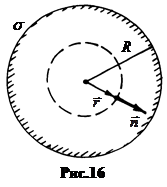ए। क्षेत्र के अंदर हम त्रिज्या के मानसिक रूप से मनमाने ढंग से केंद्रित क्षेत्र बनाकर पाते हैं आर < आर (चित्र .16)। चूंकि डिज़ाइन किए गए क्षेत्र में शून्य शुल्क शामिल है (इसके अंदर कोई शुल्क नहीं है), फिर वेक्टर का प्रवाह इ।
एक मनमाने ढंग से क्षेत्र के माध्यम से शून्य है। । (4.5)
क्षेत्र के भीतर किसी भी आंदोलन की संभावना की वृद्धि शून्य है, 
। इसलिए, सभी बिंदुओं की क्षमता इंडोर स्पेस गोलाकार क्षेत्र की क्षमता के समान और बराबर हैं। के लिये आर < आर । इसलिए,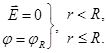 
(4.6)
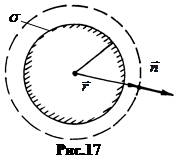बी माध्यम के बाहर का क्षेत्र हम मानसिक रूप से इसके चारों ओर, त्रिज्या के मनमाना केंद्रित क्षेत्र का निर्माण करके पाते हैं आर > आर (चित्र .17)। स्ट्रीम वेक्टर इ।
इस मामले में 
, (4.7)
भौतिक क्षेत्र में पूर्ण प्रभार कहां है। यहां से
. (4.8)
क्षेत्र के बाहर चार्ज किए गए क्षेत्र का क्षेत्र वही है जैसे कि उसके सभी चार्ज अपने ज्यामितीय केंद्र के बिंदु पर केंद्रित थे। इसलिए क्षेत्र के बाहर चार्ज किए गए क्षेत्र के क्षेत्र की क्षमता एक बिंदु शुल्क की संभावना के समान ही है।
इसलिए,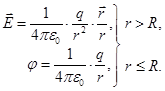 
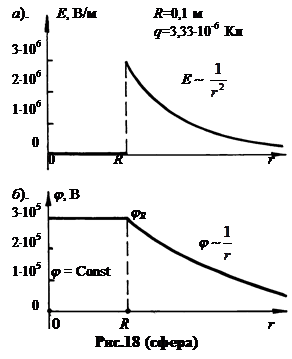
इसके अंदर और बाहर चार्ज किए गए क्षेत्र के क्षेत्र को शेड्यूल द्वारा सचित्र किया जा सकता है। Fig.18-ए (शीर्ष पर) एसआई अध्यादेशों के (शीर्ष पर), क्षेत्र के केंद्र से निर्मित त्रिज्या वेक्टर पर डिजाइन वेक्टर डिजाइन स्थापित करना। Fig.18-B (नीचे) - संभावित में। गोलाकार त्रिज्या आर चार्ज सकारात्मक चार्ज ताकि इसकी बाहरी सतह के पास फ़ील्ड की ताकत 3 × 10 6 वी / मीटर है।
यदि क्षेत्र चार्ज किया जाता है ऋणात्मक आवेशग्राफ क्षैतिज अक्ष के प्रति दर्पण-सममित रिश्तेदार होंगे।
उदाहरण 4.2। एक ठोस समान रूप से चार्ज कटोरे का क्षेत्र। दिखाए गए योजना के तहत दोहराते हुए, हम पाते हैं कि चार्ज की गई गेंद के बाहर का क्षेत्र बिल्कुल वैसा ही है जैसा कि उसका शुल्क अपने ज्यामितीय केंद्र (फॉर्मूला 4.9, 4.10) में केंद्रित था।
किसी भी मानसिक सांद्रिक क्षेत्र के लिए गेंद के अंदर (चित्र 1 9) हमें मिलता है:
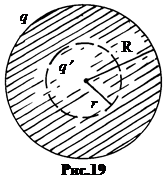
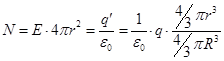। यहां से 
. (4.11,12)
यहाँ q ¢ - त्रिज्या क्षेत्र के भीतर संलग्न चार्ज आर। यह मानसिक क्षेत्र की मात्रा के अनुपात पर बल्क की मात्रा के अनुपात पर एक गेंद के पूरे प्रभार के काम की तरह है।
समान रूप से चार्ज कटोरे के अंदर तनाव शून्य तक केंद्र में कम हो जाता है।
गेंद के अंदर फील्ड पॉइंट की क्षमता को खोजने के लिए, हम क्षेत्र की सतह पर मानसिक क्षेत्र की सतह से एक परीक्षण शुल्क की इकाई को स्थानांतरित करने के काम की गणना करते हैं (हम एक परीक्षण शुल्क और एक गेंद के चार्ज मानते हैं सकारात्मक)। । (4.13)
जैसा जे आर - गेंद की सतह की क्षमता, फिर, सूत्र (4.10) के अनुसार इसे व्यक्त करना, जहां आर = आर, और समानता के दाईं ओर चले गए, हम दूरी पर गेंद के अंदर के क्षेत्र की क्षमता के लिए एक अभिव्यक्ति प्राप्त करते हैं आर उसके केंद्र से।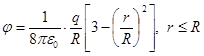 
. (4.14)
इसलिए,
(1.15,16)
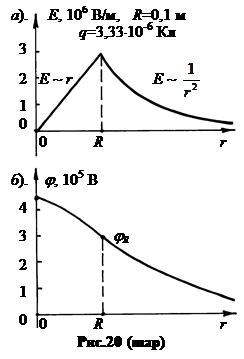
Fig.20 वेक्टर अनुमान दिखाता है इ। त्रिज्या वेक्टर (शीर्ष पर) और संभावित पर जे। (नीचे) एक सकारात्मक चार्ज कटोरे के अंदर और परे अंतरिक्ष के लिए। गेंद के केंद्र में, तनाव शून्य है, और क्षमता परिमाण में अधिकतम है। यद्यपि गेंद की सतह पर तनाव में अंतर नहीं है (चार्ज किए गए क्षेत्र के विपरीत), लेकिन इसके व्युत्पन्न में एक अंतर है, परिमाण और संकेत पर बदल रहा है। गेंद की सतह पर संभावित और इसके व्युत्पन्न में कोई अंतर नहीं है।
उदाहरण 4.3। क्षेत्र चार्ज किया गया अनंत विमान । सतह घनत्व प्रभार एस = const।.
इस तथ्य से कि क्षेत्र में समरूपता का विमान है, यह वेक्टर की रेखाएं हैं इ। सामान्य चार्ज विमान। इसलिए, फ़ील्ड की गणना करने के लिए, एक सीमित आधार क्षेत्र के साथ एक बेलनाकार मात्रा का चयन करें एस ताकि बनाने वाले सिलेंडर लाइनों के समानांतर थे इ। । फिर फ्लो वेक्टर इ। साइड सतह के माध्यम से शून्य (Fig.21) है।
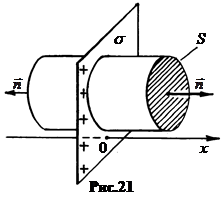स्ट्रीम वेक्टर इ।
इस सिलेंडर की सतह के माध्यम से
, (4.17)
कहा पे इ। - सिलेंडर के आधार बिंदुओं पर क्षेत्र की ताकत। गॉस प्रमेय के अनुसार। चूंकि हमें मिलता है। या वेक्टर रूप में। (4.18)
यहां सिलेंडर के आधार के लिए सामान्य का एक ही वेक्टर है, जो बाहर निर्देशित है।
एक अनंत चार्ज विमान का क्षेत्र पूरी जगह में समान है और दूरी के साथ कम नहीं होता है।
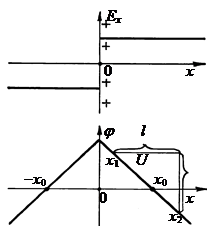
संभावित गणना के लिए जे। ऐसा हमारा विश्वास है जे। \u003d 0 अनंत पर नहीं, और विमान से कुछ दूरी पर एच 0। इसलिए समन्वय के साथ क्षेत्र के किसी भी बिंदु की क्षमता एच बिंदु से इकाई चार्ज के आंदोलन की गणना है एच बिल्कुल सही एच 0। तब से। (4.1 9)
तब से 
. (4.20)
वोल्टेज यू किसी भी दो बिंदुओं के बीच एकरूप क्षेत्र, जहां - फील्ड लाइन के साथ उनके बीच की दूरी बराबर है, (4.21)
|
|
उदाहरण 4.4। असीम रूप से चार्ज किए गए धागे का क्षेत्र। चार्ज किए गए धागे के खंड की तीव्रता की गणना करने का कार्य उदाहरण 3.2 में सामान्य रूप में हल किया जाता है। यहां हम गॉस प्रमेय का उपयोग करके कार्य को हल करेंगे। एक असीमित सीधे धागे को समान रूप से एक रैखिक चार्ज घनत्व के साथ चार्ज किया जाता है टी,[टी] \u003d सीएल / एम। जाहिर है, फ़ील्ड में अक्षीय समरूपता है, और बिजली लाइनों को त्रिज्या के लंबवत त्रिज्या के साथ निर्देशित किया जाता है। एक मात्रा के रूप में, सतह के माध्यम से हम वेक्टर के प्रवाह की गणना करेंगे इ। , रोटेशन सिलेंडर लें, जिसकी धुरी धागे (चित्र 23) के साथ मेल खाता है।
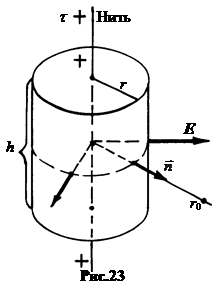यदि सिलेंडर ऊंचाई एच, फिर सिलेंडर की तरफ की सतह के माध्यम से तनाव के वेक्टर की धारा
. (4.22)
(वेक्टर स्ट्रीम इ। सिलेंडर के आधार के माध्यम से शून्य है)। यहां से। (4.23)
क्षेत्र की क्षमता को खोजने के लिए, हम बिंदु से क्षेत्र के क्षेत्र के कारण एक ही चार्ज को स्थानांतरित करने के काम की गणना करते हैं आर मुद्दे पर आर 0। तब से
. (4.24)
या 
. (4.25)
उदाहरण 4.3 के रूप में, शून्य क्षमता का बिंदु अनंत तक स्थानांतरित नहीं किया जा सकता है, क्योंकि किसी भी बिंदु के बीच वोल्टेज आर बिंदु आर 0 \u003d ¥ असीम रूप से बड़ा हो जाता है।
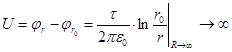. (4.26)
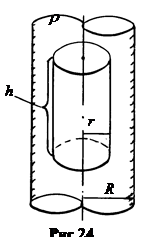
उदाहरण 4.5। एक सीधा चार्ज ठोस सिलेंडर का क्षेत्र। अनंत त्रिज्या सिलेंडर चलो आर घनत्व का आरोप लगाया आर। तनाव की गणना करने के लिए इ। एक दूरी पर सिलेंडर के अंदर आर < आर धुरी से, मानसिक रूप से एक कोएक्सियल सिलेंडर ऊंचाई का निर्माण एच और त्रिज्या आर (Fig.24)।
चूंकि सिलेंडर के अंदर और बाहर के क्षेत्र में अक्षीय समरूपता होती है, इसलिए बिजली की रेखाएं सिलेंडर की धुरी के लिए लंबवत होती हैं और त्रिज्या के साथ निर्देशित होती हैं। इसलिए, वेक्टर का प्रवाह इ।
काल्पनिक सिलेंडर के आधार के माध्यम से शून्य है। पूरा प्रवाह पक्ष की सतह के माध्यम से चला जाता है। 
. (4.27)
यहां से 
. (4.28)
गेंद (उदाहरण 4.2) के रूप में, सिलेंडर के अंदर का क्षेत्र समान रूप से सिलेंडर की धुरी में कमी आती है।
सापेक्ष सतह के सिलेंडर के अंदर क्षेत्र के बिंदुओं की क्षमता समानता के एकीकरण द्वारा पाया जाता है - डीजे। = ईडीआर एक के भीतर आर इससे पहले आर.
. (4.29)
यहां से 
. (4.30)
यहाँ जे आर - किसी बिंदु के सापेक्ष सिलेंडर की सतह की क्षमता आर 0, जहां क्षमता शून्य के लिए स्वीकार की जाती है। मूल्य जे आर फॉर्मूला (4.26) द्वारा स्थित है, जहां आर = आर, टी = आरपीआर। 2 .
3. क्षेत्र की गणना करें - इसका मतलब ज्ञात वितरण है विद्युत प्रभार अंतरिक्ष में, क्षेत्र की ताकत की गणना करें इ। या संभावित जे।। अक्सर संभावित क्षमता की गणना आसान होती है क्योंकि यह एक स्केलर है। इसलिए, बिजली के सिद्धांत में, तथाकथित कुल कार्य इलेक्ट्रोस्टैटिक्स, यानी, विस्तारित विद्युत चार्ज निकायों सहित स्थिर चार्ज सिस्टम द्वारा बनाए गए विद्युत क्षेत्र की क्षमता की गणना करने का कार्य।
गणितीय शर्तों में, अंतरिक्ष के क्षेत्रों में इलेक्ट्रोस्टैटिक्स का समग्र कार्य लैपलेस डी समीकरण के समाधान में कम हो जाता है जे। \u003d 0, जहां डी एक दूसरा क्रम विभेदक ऑपरेटर (लैपलेस ऑपरेटर) है। कार्टेशियन निर्देशांक में, इसमें फॉर्म है: 
.
समारोह की सीमा की स्थिति के तहत समीकरण हल किया जाता है जे। सभी चार्ज निकायों की सतह पर जाना जाता है, और उनके बीच कोई मुफ्त शुल्क नहीं है। यह तथाकथित एज कार्य है।
1) विद्युत प्रभार और उनकी बातचीत, कौलॉन का कानून।
इलेक्ट्रिक चार्ज इन शुल्कों द्वारा बनाए गए इलेक्ट्रोस्टैटिक क्षेत्रों के माध्यम से अन्य चार्ज निकायों के साथ बातचीत करने के लिए निकायों की संपत्ति निर्धारित करता है।
निकायों की बातचीत सकारात्मक हो सकती है (यदि निकाय / शुल्क आकर्षित होते हैं) और नकारात्मक (यदि निकाय / शुल्कों को पीछे छोड़ दिया जाता है)।
स्पष्ट रूप से एक प्राथमिक प्रभार का अस्तित्व। उनके पास अधिकांश कण (प्रोटॉन, पॉजिट्रॉन, इलेक्ट्रॉन) हैं।
प्रभार इस तरह के प्राथमिक शुल्कों की एक पूर्णांक संख्या के बराबर है।
यदि शुल्क अभी भी है, तो यह प्रोस्टाटा में एक इलेक्ट्रोस्टैटिक क्षेत्र बनाता है। यदि चार्ज त्वरण के बिना आगे बढ़ रहा है - चुंबकीय क्षेत्र भी। यदि त्वरण के साथ आगे बढ़ना एक विद्युत चुम्बकीय क्षेत्र है जो विद्युत चुम्बकीय तरंगों के रूप में फैलता है।
बिंदु प्रभार एक चार्ज शरीर है, जिसमें रैखिक आयामों को उपेक्षित किया जा सकता है।
दो आरोपों की बातचीत की ताकत कोनॉन के कानून द्वारा निर्धारित किया जाता है:
1. चार्ज पूरी लंबाई के साथ समान रूप से वितरित किया जाता है।
चार्ज की रैखिक घनत्व की अवधारणा पेश की गई है।
2. चार्ज चार्ज शरीर की सतह पर समान रूप से वितरित किया जाता है।
चार्ज की सतह घनत्व की अवधारणा पेश की गई है।
3. चार्ज पूरे वॉल्यूम में समान रूप से वितरित किया जाता है।
चार्ज की थोक घनत्व की अवधारणा पेश की गई है।
2) तनाव - शक्ति विशेषताइस क्षेत्र से अभिनय बल के अनुपात के बराबर इस बिंदु पर लगाए गए बिंदु शुल्क तक।
दिशा दिशा के साथ मेल खाती है
विद्युत क्षेत्र विद्युत चुम्बकीय क्षेत्र के घटकों में से एक है, एक विशेष वीडियो सामग्री, जो निकायों या कणों के आसपास मौजूद है, जो विद्युत चार्ज है, साथ ही साथ बदलते समय एक मुक्त रूप में भी है चुंबकीय क्षेत्र (उदाहरण के लिए, विद्युत चुम्बकीय तरंगें)। बिजली क्षेत्र सीधे अदृश्य, लेकिन चार्ज निकायों पर अपने बिजली के प्रभाव के कारण मनाया जा सकता है।
बिंदु प्रभार का तनाव क्षेत्र।
निरूपित: प्रश्न - एक शुल्क जो क्षेत्र बनाता है,
क्यू 0 - क्षेत्र में रखा गया शुल्क (बाहरी प्रभार)।
कूल का कानून :. क्षेत्र तनाव :.
फिर स्पॉट चार्ज फ़ील्ड का तनाव:
सुपरपोजिशन का सिद्धांत।
यदि अंतरिक्ष के बिंदु पर कई शुल्कों द्वारा बनाए गए फ़ील्ड हैं, तो इस फ़ील्ड बिंदु पर तनाव क्षेत्र की ताकत के वेक्टर योग के बराबर है।
|
3) तनाव के वेक्टर की धारा कहा जाता है। सर्किट क्षेत्र पर तीव्रता वेक्टर के मॉड्यूलस के उत्पाद के बराबर एफ का मान, जो कुछ क्षेत्र को सीमित करता है, और तनाव वेक्टर और सामान्य (लंबवत) के बीच कोण के कोसाइन पर साइट पर। | |
|
अगर हम मानते हैं कि तनाव सतह के प्रति इकाई क्षेत्र की शक्ति रेखाओं की संख्या के आनुपातिक है (यानी मोटाई), तो स्ट्रीम स्ट्रीम इस सर्किट को पार करने वाली पावर लाइनों की कुल संख्या के आनुपातिक है। |
प्रमेय गौसा - इलेक्ट्रोडायनामिक्स का मुख्य प्रमेय, जिसका उपयोग विद्युत क्षेत्रों की गणना करने के लिए किया जाता है, मैक्सवेल समीकरणों की प्रणाली में प्रवेश करता है। यह बंद सतह के माध्यम से बिजली के क्षेत्र की ताकत की धारा और इस सतह तक सीमित मात्रा में चार्ज के बीच संबंध व्यक्त करता है।
गॉसियन प्रमेय। एक बंद सतह के माध्यम से तनाव वेक्टर की धारा माध्यम और बिजली की पारगम्यता द्वारा विभाजित शुल्कों की इस राशि द्वारा कवर किए गए शुल्कों की बीजगणितीय राशि के बराबर होती है। लगातार।
Ostrograd फॉर्मूला के काम में निम्नलिखित रूप में दर्ज किया गया है:
जहां ω I. एस - क्रमशः मात्रा और सतहों के विभेदक। आधुनिक रिकॉर्ड में ω \u003d डीΩ - मात्रा का तत्व, एस = डीएस। - सतह का तत्व। - अंतरिक्ष के एक बंद क्षेत्र में अपने विशेष प्रथम-क्रम डेरिवेटिव के साथ निरंतर कार्य, एक बंद चिकनी सतह द्वारा सीमित।
4) प्रमेय का उपयोग किया जाता है इलेक्ट्रोस्टैटिक क्षेत्रों की गणना।
1. एक असीम रूप से लंबे चार्ज सिलेंडर का क्षेत्र।
चार्ज पूरी लंबाई पर वितरित किया जाता है
2. चार्ज किए गए क्षेत्र का क्षेत्र।
चार्ज पूरी सतह पर वितरित किया जाता है 
चार्ज पूरे वॉल्यूम में वितरित किया जाता है
3. फ्लीली चार्ज प्लेन
एक अनंत सजातीय चार्ज किए गए विमान द्वारा बनाए गए एक क्षेत्र पर विचार करें। उसी के विमान के चार्ज की सतह घनत्व और σ के बराबर। एक मानसिक रूप से एक सिलेंडर की कल्पना करें, बनाने के साथ, विमान के लंबवत, और आधार δ एसविमान के सापेक्ष सममित रूप से स्थित है। समरूपता द्वारा इ।" = इ।"" = इ।। स्ट्रॉय वेक्टर प्रवाह 2 है इ।Δ एस। गॉस प्रमेय को लागू करना, हमें मिलता है:
किस से
5) एक स्थायी विद्युत क्षेत्र की क्षमता।
प्राथमिक आंदोलन डीएल पर बल का काम बराबर है
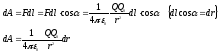
बिंदु 1 से बिंदु 2 तक q 0 को स्थानांतरित करते समय काम करें।
यह आंदोलन के प्रक्षेपवक्र पर निर्भर नहीं है। नतीजतन, el.stat। प्वाइंट चार्ज का क्षेत्र संभावित है, और el.stat। रूढ़िवादी बल।
किस में संभावित या तो बिंदु el.stat। खेत हैं भौतिक मात्रासंभावित ऊर्जा सकारात्मक आरोपइस बिंदु पर रखो।
बिंदु 1 से बिंदु 2 तक एक सकारात्मक चार्ज को स्थानांतरित करते समय दो बिंदुओं की संभावनाओं में अंतर काम के बराबर होता है।
प्वाइंट चार्ज के स्ट्रॉय इलेक्ट्रिक फ़ील्ड
गॉस फॉर्मूला - ओस्ट्रोग्राड्स्की के अनुसार, साथ ही एक्सवेल के समीकरण का उपयोग करके, इसे प्राप्त करना आसान है:
कहा पे प्र में। - एक बंद सतह के अंदर चार्ज, वॉल्यूम वी। एकीकरण की सतह के रूप में, दायरे (केंद्रीय समरूपता) ले लो, तो
एक डॉट चार्ज फ़ील्ड की केंद्रीय समरूपता के कारण:
6) संभावित, तनाव और क्षमता के बीच संचार।
क्षमता -क्षेत्र की ऊर्जा विशेषताओं, संख्यात्मक रूप से उस कार्य के बराबर है जो इस बिंदु से इस बिंदु से इन्फिनिटी में स्थानांतरित करने के लिए किए जाने की आवश्यकता है।
इस तथ्य को देखते हुए कि काम है स्केलर मूल्य, और संभावित एक स्केलर है।
क्षमता की अवधारणा के लिए पेश किया जा सकता है इलेक्ट्रोस्टैटिक क्षेत्र इस तथ्य को ध्यान में रखते हुए कि चार्ज के आंदोलन पर काम प्रक्षेपण के रूप में निर्भर नहीं है, जिसके अनुसार स्थानांतरण किया जाता है, लेकिन केवल बिंदु की स्थिति पर।
ई। वेक्टर परिसंचरण बंद समोच्च के साथ शून्य है।
प्रसार - स्केलर क्षमता की शुरूआत के लिए आवश्यक और पर्याप्त स्थिति। सबूत आंदोलन के प्रकार और प्रक्षेपण के रूप में काम की स्वतंत्रता है।
यह गणितीय रूप से इस प्रकार है क्षमता - विद्युत क्षेत्र की ताकत से अभिन्न। इसलिए, तनाव क्षमता से लिया गया है।
फिर, अंतरिक्ष में केंद्रित क्या है, इस पर विचार करते हुए,
"माइनस" का अर्थ है कि वर्तमान बल (तनाव) को कम करने की संभावना की दिशा में निर्देशित किया जाता है, यानी, जहां संभावित ऊर्जा चार्ज का सबसे छोटा मूल्य होगा।
सुसंगत सतह - किसी भी संभावित वेक्टर फ़ील्ड पर लागू अवधारणा, उदाहरण के लिए, एक स्थिर विद्युत क्षेत्र या न्यूटनियम गुरुत्वाकर्षण क्षेत्र में। सुसंगत सतह - यह एक सतह है जिस पर इस संभावित क्षेत्र की स्केलर क्षमता निरंतर मूल्य लेती है।
तीन-आयामी में समीकरण आकार लेता है:
में कार्तीय समन्वय प्रणाली लैपलेस ऑपरेटर फॉर्म में लिखा गया है और पोइसन समीकरण फॉर्म लेता है।
