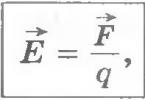Federal State Educational Institution

higher vocational education

"Rostov State University of Civil Engineering"

Approved

Head Department of Physics

__________________ / N.N. Kharabayev /

Teaching guide

ABSTRACT OF LECTURES in Physics

(for all specialties)

Rostov-on-Don

Teaching manual. Summary of lectures on physics (for all specialties). - Rostov n / D: Growth. state builds University, 2012. - 103 p.

The abstract of lectures on physics, based on the textbook of T.I. Trofimova "Course of Physics" (publishing house Higher School).

Consists of four parts:

I. Mechanics.

Ii. Molecular physics and thermodynamics.

Iii. Electricity and magnetism.

Iv. Wave and quantum optics.

Designed for teachers and students as a theoretical accompaniment of lectures, practical and laboratory classes in order to achieve a deeper mastery of the basic concepts and laws of physics.

Compiled by: prof. N.N. Kharabayev

assoc. E.V.Chebanova

prof. A.N. Pavlov

Editor N.Е.Гладких

Templan 2012, pos. Signed to print

Format 60x84 1/16. Paper writing. Risograph. Uch.-iz.d. 4.0.

Circulation 100 copies. Order

_________________________________________________________

Editorial and publishing center

Rostov State Construction University

334022, Rostov-on-Don, ul. Socialist, 162

© Rostov State

university of Civil Engineering, 2012

Part I. Mechanics

Topic 1. Kinematics of translational and rotational motion. Forward motion kinematics

The position of the material point BUTin the Cartesian coordinate system at a given time is determined by three coordinates x, y and zor radius vector- vector drawn from the origin of the coordinate system to a given point (Fig. 1).

The motion of a material point is determined in a scalar form by kinematic equations: x = x (t),y = y (t),z = z (t),

or in the vector equation:.

Trajectory   the movement of a material point is the line described by this point as it moves in space. Depending on the shape of the trajectory, the movement can be straight or curvilinear.

The material point, moving along an arbitrary path, for a small period of time D tmove from position BUTin position ATwhile passing the path D sequal to the length of the path section AB(Fig. 2).

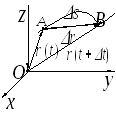
Fig. 1 Fig. 2

Vector drawn from the initial position of the moving point at the moment of time t   to the final position of the point at time (t+ D t) is called by movementi.e .

Medium Speed ​​Vector   called the ratio of moving to the time interval D t For which this move occurred:

The direction of the average velocity vector coincides with the direction of the displacement vector.

Instant speed   (speed at time t) is called the limit of the relationship of movement to the time interval D tfor which this movement occurred, with the pursuit of D t   to zero: = ℓim Δt → 0 Δ / Δt = d / dt =

The instantaneous velocity vector is directed tangentially at a given point to the trajectory in the direction of motion. As the time span aspiresD t   to zero the modulus of the displacement vector tends to the path valueD s, therefore, the module of vector v can be defined via path D s: v = ℓim Δt → 0 Δs / Δt = ds / dt =

If the velocity of a point changes with time, then the rate of change of the velocity of a point’s movement is characterized by acceleration.

Average acceleration    ‹A› in the time interval from t   before ( t   + D t) is called a vector quantity equal to the ratio of the change in speed () to the time interval D tfor which this change occurred: = Δ / Δt

Instant acceleration   or acceleration   point motions at time t   called the limit of the ratio of the speed change to the time interval D tfor which this change has occurred, with the pursuit of D t    to zero:

,

where is the first derivative of the function by time t,

–Second time function t.

These derivatives are usually denoted respectively in the form: and.

The acceleration vector can be decomposed into two components: tangential and normal, that is:

Tangential component   determines the rate of change of the velocity modulus:.

The vector is directed tangentially to the trajectory of motion and for accelerated motion coincides with the direction of the velocity vector, and for slow motion it is opposite to the velocity vector.

Normal component   determines the speed of changing the direction of speed v: a n = v 2 / r, where r – radius of curvature of the motion path.

The vector is directed along the normal to the trajectory of movement to the center of its curvature (therefore, the normal component of acceleration is also called the centripetal acceleration).

M .: Science. Ch. ed. Phys.-Mat. Lit., 1989. -352 p.

The content and location of the material correspond to the program of the course "Physics" for engineering and technical specialties of higher educational institutions, approved by the Educational and Methodological Administration for Higher Education of the Ministry of Higher Education of the USSR. The main attention is paid to the clarification of physical laws and their conscious application. The new course differs significantly from the "Course of General Physics" of the same author (M .: Nauka, 1986-1988) by the selection of the material, the level and method of presentation.

For students and teachers of higher technical educational institutions; can be used by students of other universities.

Format:    djvu / zip

The size:   4 MB

/ Download file

PART 1
  PHYSICAL BASES OF CLASSICAL MECHANICS
Chapter 1. Kinematics of the material point ...... 11
§ 1. Mechanical movement ............ 11
  § 2. Vectors .................. 15
  § 3. Speed ​​.................. 21
  § 4. Acceleration .................. 27
  § 5. Translational motion of a rigid body ..... 31
  Examples of solving problems .............. 33
Chapter 2. The dynamics of the material point ...... 34
§ 6. Inertial reference systems. The law of inertia ... 34
  § 7. Strength and mass ................ 36
  § 8. The second law of Newton ............ 38
  § 9. Units and dimensions of physical quantities ... 39
  § 10. The third law of Newton ............ 43
  §eleven. Forces ................... 44
  § 12. Gravity and weight ............. 44
  § 13. Elastic forces ................ 47
  § 14. Friction forces ................ 51
  Examples of solving problems .............. 54
Chapter 3. Laws of conservation ........... 56
§ 15. Conserved values ​​........... 56
  § 16. The law of conservation of momentum .......... 57
  § 17. Energy and work .............. 60
  § 18. Scalar product of vectors ........ 6J
  § 19. Kinetic energy and work ........ 62
  § 20. Work ................... 64
  § 21. Conservative forces ............. 67
  § 22. Potential energy of a material point in an external force field.71
  § 23. Potential energy of interaction ...... 75
  § 24. The law of conservation of energy ........... 79
  § 25. Impact of bodies ............... 81
  § 26. Moment of power ................ 84
  § 27. The law of conservation of angular momentum ...... 88
  Examples of solving problems .............. ^ 2
Head 4. Solid mechanics ......... 94
§ 28. Kinematics of rotational motion ....... 94
  § 29. Plane motion of a rigid body ........ 97
  § 30. Movement of the center of mass of a solid 1sl ...... 99
  § 31. Rotation of a rigid body around fixed poles. . 101
  § 32. Moment of inertia ............... 104
  § 33. Kinetic energy of a rotating body ..... 108

§ 34. The kinetic energy of the body during plane motion. .110
  § 35. Gyroscopes ................. 112
  Examples of solving problems .............. software
Chapter 5. Non-inertial reference systems ...... 118
§ 36. Inertia forces ................ 118
  37. Centrifugal force of inertia .......... 122
  § 38. Coriolis force ............... 125
  Examples of solving problems .............. 13.)
Chapter 6. Fluid mechanics .......... 131
§ 39. Description of the movement of liquids ......... 31
  § "10. The Bernoulli equation. .......... 31
  § 41. Fluid outflow from the orifice ........ 33
  § 42. Viscosity. Fluid flow in pipes ...... 140
  § 43. Movement of bodies in liquids and gases ....... 47
  Examples of solving problems .............. 152
Chapter 7. Elements of the special theory of relativity. 153
§ 44. Galilean principle of relativity ...... 153
  § 45. Postulates of the special theory of relativity. . 156
  § 46. Lorentz transformations. . ....... 158
  § 47. Corollaries of the Lorentz transformations ...... 162
  § 48. Interval ...... ........... 168
  § 49. Transformation and addition of velocities ...... 171
  § 50. Relativistic impulse .... ....... 173
  § 51. Relativistic expression for energy ..... 176
  § 52. Interrelation of mass and energy of rest ....... 180
  § 53. Particles with zero mass ........... 182
  $ 54. Limits of applicability of Newtonian mechanics. . 183
  Examples of solving problems .............. 185
Chapter 8. Gravity ............... 187
§ 55. The law of world wideness .......... 187
  § 53. Gravitational field ............. 191
  § 57. Cosmic velocities ............. 193
  58. It is clear about the general theory of relativity .... 195
  Examples of solving problems .............. 205

PART 2
  BASES OF MOLECULAR PHYSICS AND THERMODYNAMICS
Chapter 9. Molecular-kinetic theory ..... 207
§ 59. Statistical physics and thermodynamics ..... 207
  § 60. The state of the thermodynamic system. Process. . 209
  § 61. Mental kinetic representations ..... 211
  62. The equation of state of an ideal gas ...... 214
  § 63. Gas pressure on vessel wall ......... 217
  § 64. Average energy of molecules ........... 222
  Examples of solving problems .............. 226
Chapter 10. The first law of thermodynamics ...... 227
§ 65. Internal energy of the thermodynamic system. . 227

§ 66. Work done by the body when its volume changes 228
  § 67. The first law of thermodynamics ......... 231.
  § G8. Internal energy and heat capacity of an ideal gas 234
  § 69. The adiabatic equation for an ideal gas ....... 238
  § 70. Political processes ........... 241
§ 71. Work done by an ideal gas in various processes ... 243
  § 72. Classical theory of heat capacity of an ideal gas 245.

Examples of solving problems ..............- 49
Chapter 11. Statistical Distributions ...... 250
§ 73. Probability distribution function ....... 250
  § 74. Maxwell distribution ........... 253
  § 75. Barometric formula ........... 262
  § 76. Boltzmann distribution ........... 264
  § 77. Definition of the Perronum Avogadro constant .... 268
  Examples of solving problems .............. 263
Chapter 12. Transport phenomena ........... 209
§ 78-. The length of the free path of the molecules ....... 269
  § 79. Empirical equations of the transference phenomenon .... 274

§ 80. Molecular-kinetic theory of transport phenomena in gases. 279
  Examples of solving problems .............. 283
Chapter 13. The second law of thermodynamics ...... 239
§ 81. Micro and macro states. Statistical weight. . . 28E
  § 82. Entropy .................. 232
  § 83. Entropy of an ideal gas ........... 2-) 8
  84. The second law of thermodynamics ......... 293
  § 85. Efficiency of the heat engine 300
  § 86. .Carnot cycle ................ ЗсЗ
  Examples of solving problems .............. 307
Chapter 14. Real Gases ............ 308
§ 87. Van der Waals equation .......... 303
  § 88. Experimental isotherms .......... ° "!)
  § 89. Phase transformations ............. 32 |
  Examples of solving problems .............. 325
Chapter 15. Solid and liquid states ....... 326
§ 90. Distinctive features of the crystalline state 325
  § 91. Physical types of crystals .......... 3\u003e! 9
  § 92. The structure of liquids ............. 331
  § 93. Surface tension ........... 332
  § 94. Capillary phenomena ............. 337
  Examples of solving problems .............. 341
  Index of names ............... 343
  Subject Index .............. 344

Savelev Igor Vladimirovich

(04.02.1913–03.03.1999)

  The whole era in teaching physics in technical universities of our country is connected with the name of Igor Vladimirovich Savelyev. He is the creator and head of the original pedagogical school, the foundation of which is his well-known three-volume textbook on the course of general physics for technical colleges. The success of Russian specialists in the field of physical and technical sciences is largely due to the fact that tens of thousands of students studied general physics from the textbook by I. V. Saveliev, which he improved over 35 years - until the last days of his life.

In 1938, I.V. Saveliev graduated from the Physics Department of the Physics and Mathematics Faculty of Kharkov State University. A. M. Gorky specialty "Solid State Physics". During his studies, he worked as an intern in the cryogenic laboratory of the Kharkov Ukrainian Physico-Technical Institute.

  I. V. Saveliev - participant of the war from the first to the last of her days. After demobilization in July 1946, I. V. Savelyev joined the Laboratory No. 2 (now the RRC Kurchatov Institute) at the Department of Thermal Control Devices (now the Institute of Molecular Physics of the RRC). Under the leadership of I. K. Kikoin, the department dealt with the problem of uranium isotope separation by the gas diffusion method. Within the framework of this problem, I. V. Savelyev investigated the kinetics of reactions of uranium hexafluoride with the surfaces of various materials.

  For the cycle of works carried out in this field, I. V. Savelyev was awarded the title of laureate of the Stalin Prize of the USSR II degree (1951), “for fulfilling the special task of the government”, and awarded the Order of Lenin (1951). In 1952 he was awarded the degree of Doctor of Physical and Mathematical Sciences. However, the main business of the life of I. V. Saveliev was the teaching of physics, he devoted entirely the last 47 years of his life to this.

I. Saveliev began his pedagogical activity at the Moscow Engineering Physics Institute in 1952 at the Department of General Physics as a professor, in 1955 he became a full-time employee of the institute. From 1956 to 1959 Igor Vladimirovich was the vice-rector of the Moscow Engineering Physics Institute for Academic Affairs. In 1957, he was elected head of the department of general physics, which he headed for 28 years. In honor of I. V. Saveliev, a large physical audience of the A-304 MEPI is now named after him.

Under the guidance and with the direct participation of I.V. Savelyev, on the basis of the Faculty of Experimental and Theoretical Physics, MEPhI, the Faculty of Advanced Studies of Physics Teachers of Higher Education Institutions was established.

The three-volume General Physics Course written by him for technical universities with an expanded program was published only in Russian 9 times, with a total circulation of more than 4 million copies. He also penned a three-volume "Course of Physics" for technical universities with a regular program, a "Collection of questions and problems of general physics", a two-volume book "Fundamentals of Theoretical Physics." These textbooks have been translated and repeatedly published in mass editions in the languages ​​of almost all former Soviet republics. They were also translated into English, French, Spanish, Polish, Vietnamese, Afghan (Dari) and Arabic.

The scientific and pedagogical activity of I. V. Savelyev was marked by high government awards: the Order of Lenin (1951), two orders of the Badge of Honor (1954, 1966), he was also awarded the Order of the Patriotic War of the II degree (1985) and many medals.

Since 1985, Igor Vladimirovich was a professor-consultant in the department of general physics at MEPhI. Until the last days of his life, he worked actively, generously sharing his experience, improving and preparing his books for reprinting. None of the books of Savelyev came out as a stereotyped publication.

Lectures on physics by VI Babetsky

(II course of the faculty "Applied Mathematics and Physics" MAI) 1999.

Uh electromagnetic interaction

The world consists of interacting particles. Everything that we see is built from elementary particles, there are such building blocks of the universe. At the macroscopic level, there are many interactions; in fact, there are four types of fundamental interactions at the base of everything. They're called:

1) strong

2) electromagnetic,

3) weak,

4) gravitational.

They are listed in decreasing order of interaction strength.

Strong interaction determines the structure of atomic nuclei and deeper structures. The following is electromagnetic interaction. It is weaker by two orders of magnitude. Strong interaction is manifested at small distances, cm, electromagnetic interaction is manifested at any distances. Then there is a weak interaction, in general, playing an imperceptible role at the macroscopic level. And, finally, the weakest gravitational interaction, about forty orders of magnitude weaker than the electromagnetic one. But why we feel the gravitational interaction more often, for example, you want to jump, and you are pulled down. This is due to the fact that all particles participate in it.

These interactions are characterized by the fact that certain particles participate in them, particles possessing certain properties.

At the macroscopic level, the electromagnetic interaction is the most important, this is what we see on Earth - this is all the electromagnetic interaction.

Electric charge

Particles involved in the electromagnetic interaction have a special property - electric charge. What is an electric charge? Primary concept. It can not be described in other more understandable terms. Electric charge - an inherent property of an elementary particle. If there is a particle that has an electric charge, for example, an electron, the electron known to all of you, it is impossible to deprive it of this property. The electron has other properties: mass, spin, magnetic moment. There are particles and do not have this property. If a particle does not participate in electromagnetic interaction (and how to determine this? Take a particle, we find the force acting on it, there are books in which guidance is given for further actions), so if the particle does not participate in electromagnetic interaction, then it does not have an electric charge .

The charges of all bodies are multiples of C, this is the charge of an electron. This means that in nature there is a minimum charge equal to e. Could take e= 1, but for a number of reasons, in particular, for historical reasons, e   expressed by such a number.

There are such particles - quarks, whose charge is fractional:, etc. The fact that their fractional charge does not contradict what I said, since quarks are not observed on their own. It is believed that it is impossible to allocate quarks individually to get a particle with a fractional charge. To make it clearer, I will give this example. We have a magnetized knitting needle with a south and north pole, they behave like point sources of current, but having broken a needle in half, the south pole remains on one end, and the north pole pops up on the other. Similarly, when quarks are divided, they divide, but new quarks appear, not their halves.

Charges come in two characters: “+” and “-“. How to understand the negative and positive sign? One could call them other symbols, but which are included in mathematical concepts, because mathematics is a basic science.

Electromagnetic field

Once again, the world consists of interacting particles, but particles do not interact with each other. This question is still occupied by Newton. He believed that the very idea of ​​interacting through empty space is absurd. The current physics also rejects interaction through empty space. For example, from where does the Earth "know" that somewhere from it, at a distance of 150 million km, is the Sun, to which it must attract? A field is a carrier of interaction, in particular, a carrier of electromagnetic interactions is an electromagnetic field. What is a field? again the primary concept, it is impossible to express it more in simple words. It should be understood as follows: we have a charged particle, one single particle, and what the particle creates in space is the electromagnetic field. Some forms of this electromagnetic field   we see light is a manifestation of the electromagnetic field. Another charged particle is immersed in this field and interacts with this field where it is located. Thus, the problem of interaction is solved. The electromagnetic field is a carrier of electromagnetic interaction.

Again, we cannot describe the field in ordinary words. Here is a table, it is wooden, brown, etc., it can be described by an infinitely large set of properties. The electromagnetic field is a much simpler thing. The motion of a particle in an electromagnetic field is described by the following equation.

Newton's Second Law :

Charged particle with charge qthat moves in an electromagnetic field according to this equation. We see that the force acting on the particle from the electromagnetic field is determined by two vector fields: that is, at each point in space a vector is given, which can change over time (the mathematician can tell if a scalar function is given at each point in space, that is a scalar the field, if a vector function is given (the vector field is given), the field is called tension electric field , field - magnetic field induction. Why they are so called, it does not matter to us now, these are terms. Why are they separated? Because their influence on the particle is different. The field does not contain any particle characteristics except charge. If a v= 0, the second term takes off. This means that the magnetic field acts only on moving particles. Fixed charges do not feel a magnetic field.

When we talk about the functions of coordinates, we mean that we are in some inertial system. If the charge moves, it will rest in another inertial system. This means that, if only exists in one inertial reference frame, then and will appear in another. These two vector fields completely describe the electromagnetic field. To set an electromagnetic field means to set six functions of coordinates and time.

How to set the field in this room? We place trial charge, we measure force, we divide on qget Slightly more difficult to measure. There are more elegant measurement methods based on this equation. And we get a comprehensive description of this thing. This description is much simpler than the description of this table.

Field equations

Can I specifically, physically build a field? The answer, generally speaking, is no. Not every vector field can represent real electric fieldand not every vector field represents the magnetic field. The real electromagnetic field has a structure, and this structure is expressed by field equations, which act as filters.

The electromagnetic field is created by charged particles, or, in other words, charged particles are sources of an electromagnetic field.

The main objective of the theory:

charged particle distribution is presented and we have to find fieldwhich is created by these particles.

Question: how can I describe the distribution of particles, how to show the distribution of charges? By the way, no other properties other than charge are important. You can take some kind of particle, measure its charge and hang a tag on it, and so on with all the particles. But technically it is impossible to do.

Here we have some coordinate system. At a point with a radius vector, choose some element of the volume DV i, determine the charge of this element of the volume. Let the inside of this element volume is charge D q i. Now we define this value:. We will reduce the volume, while it turns out that the ratio tends to a certain limit. It is believed that the volume element is very small, but the number of particles in it is large, such is the reality.

The function defined above is called charge density. It is clear that the entire charge distribution is described by a function. If there are separate point charges, they fall under this function. And it is such that, if at a point there is a point charge, then =. The scalar function allows you to fully describe the world in terms of electrodynamics. But not only that, the speed of the charge also affects the electromagnetic field. Since the magnetic field is created by moving charges, we need to take into account more movement, and for this we need another characteristic. We take a point in our coordinate system and calculate this value:. Formulas need to learn to read narrative! In this case: catch all the particles of this volume, multiply the charge of the particle by its speed, divide by the volume, and then go to the limit, we get some vector and assign this vector to the point in the vicinity of which we measured ... We get a vector field. - current density. By the way, in mechanics a similar value is the impulse density. Instead of charge, we take the mass, we get the total impulse, if we divide it by volume, we get the impulse density.

The sources of the electromagnetic field are fully characterized by a scalar function and a vector function. I already spoke there about the flowers in the garden, the birds fly ... from the point of view of electrodynamics, the system should be described by the functions r and. Indeed, if you give these functions, then you could give them a color picture, by the way, the TV does it, and the waves that fall into your eye are part of this electromagnetic field. The task of these functions sets the field, because if sources are known, then the field is also known.

Field equations

All electricity sits in these equations. They are, in fact, symmetrical and beautiful. These equations are postulated; they underlie the theory. These are the fundamental equations of the theory. By the way, that's interesting. The theory has always existed since the seventies of the XIX century to this day, and no amendments! Newtonian theory could not stand, and electrodynamics cost about 1.5 centuries, works at a distance of m and no deviations.

To solve these equations, some mathematical constructions will be required.

Stream vector.

Some field specified , at some point in space given vector . In the vicinity of this point, select the site dS, the site is oriented, its orientation is characterized by a vector. Then the construction is called vector flow through pad dS. The ground is so small that the vector can be considered constant within this site.

Now the situation is different. Consider some piece of surface. This surface is divided into elements. For example, the selected item number iits area D S iits normal. Somewhere within the element, choose a vector, the element itself is defined by the radius-vector, that is, some point inside the element has a radius-vector. The sum over all elements of the surface forms the following sum:, and now the limit is denoted as:.

Well, this is again a standard technique: the integral is the limit of the sum by definition, the limit of this sum is called vector flow through surface S.

So, if the wind blows, at each point of a certain surface a velocity vector is determined, then the flow of the velocity vector over this surface will be the volume of air passing through the surface per unit of time. If the vector field   not a velocity field, but something else, nothing flows there. This is a certain term, and do not understand it literally.

If the surface is closed, then we divide it into small elements. But the limitation is taken: the normal vector is chosen outside (the choice of the normal affects the sign). If the surface is closed, then the normal is taken out, and the corresponding integral is supplied with a circle. This is the term flow.

If a - velocity field, scalar product   negative (see fig.2.2 figure 1 ), it is a gas or air flowing into the surface. And we take the site 2 Here the flow is positive, it is air flowing out of the surface. If we calculate such a thing for the flow of wind speed through a closed surface (it will be the difference between the air flowing in and out), and if the flow is stationary, that is, the speed does not change with time, then the integral will be zero, although not always.

If you take, then such a thing means that the mass of inflowing air is equal to the mass of flowing out.

Circulation flow.

The lines along which the field is directed are called lines of force, and for any vector field they are called integral curves. Consider some curve . Sequentially divide the curve into elements, here is one element, I select it, a small vector. Within this element, we determine the value of the vector, take the scalar product, obtain a number and sum it over all elements. In the limit we get some number: which we denote.

Take a closed curve (the integral will then be provided with a circle), set arbitrarily the direction, is a certain number depending on the vector   and called vector circulation in a closed loop.

If the wind blows, the circulation in a closed loop is not always true, is zero. And if we take a vortex, the circulation is obviously not zero.

Static electromagnetic field (electrostatics)

Last time, I drew four equations. Let's start chewing them on the sly. And make simplifications. First of all, suppose. from what? From everything, that is, nothing changes over time.

What is the peculiarity of physics? Not in the subject! All sciences have their subject matter, biology - the science of studying life on Earth, etc. Physics is different view of the world. From the point of view of electricity, it is characterized by two vector fields, by the way, if you set these things, for example, to give a description of the charges in this audience, then we will be able to restore all of the picture that you are watching.

So, . And the second.

At every point in space, nothing changes, and all the charges are fixed, that is, all the charges are nailed just with nails. Then the equations take the form:

It is with this substitution that our four fundamental equations take the form.

The third equation means that the flow of the vector through any closed surface is zero, the fourth - the circulation of the vector along any closed loop is equal to zero. From these two equations it follows that. This is not obvious, but we will get there before that. The magnetic field is absent. In a static electromagnetic field there is no magnetic field, and the electric one is described by two equations. In these equations sit all the properties electrostatic field, that is, nothing else is needed. And we will extract these properties now.

General properties of the electrostatic field

First of all, what do these equations mean? The first equation says that if we take some closed surface S, V is the volume of this surface, divide the surface into elements, determine the field strength within each element and calculate such a thing, sum it up, no one forbids us to do this, this is a mathematical thing physics sits in equality:

(the flux of the vector of tension through a closed surface) =

Thus, the flow of a vector through any closed surface is equal to the charge inside this surface.

For example, walls, floor, ceiling is a closed surface. We can count the flow through this closed surface and get a number, and if this number is non-zero, it means that there is a charge here. Electromagnetic interaction is very strong, and because of this we have a neutral substance. Zero get. This does not mean that there are no electric fields, but no charge.

We take a closed loop, calculate the circulation. The second equation states that, whatever circuit we take, the circulation is zero. It follows that power lines   Electromagnetic fields can not be closed. We could take the contour that coincides with this line, the scalar product does not change sign, therefore, the integral is not zero. Power lines can not be closed, but then what about them?

There is a certain area from which the lines of force come out, then we take a closed surface S and along this closed surface. It means that q>0.

If, on the contrary, the lines of force enter a region, this region is surrounded by a surface, then the integral is negative. The normal is directed outward, in the first case the product is positive, and here it is negative.

We can say that the lines of force of the electrostatic field begin on positive charges and end on negative or go to infinity, but it cannot be so that the line is closed in itself. For the magnetic field, we will see further that the lines of force are always closed, as opposed to electrostatic, which are never closed.

Potential

Here is a mathematical statement:.

You, here, the words must read the formulas themselves. By the way, physics can be stated without words, just like mathematics. From the fact that the circulation for any contour is zero, it follows that the vector field can be expressed through a certain function of, called the scalar field gradient:. Any scalar field j   You can put in a vector field according to this recipe. This vector field is called the scalar field gradient. j.

The meaning of the vector field. is the vector, the direction of the vector is the direction in which the function jchanging most quickly. The direction of the vector is the direction of the quickest change of the function. jand the magnitude of the vector characterizes the rate of change of the function j   in this direction. Well, speed is relative to spatial movement.

Temperature, obviously a scalar quantity. At this point, they put a thermometer, he showed something, put it in another, he would show another temperature. And now, the gradient from this scalar field. The temperature at this point is this, shifted in this direction by a meter — another temperature, and so on all sides, where the temperature is higher, its gradient will be directed there, and the magnitude of this vector.

Another example is density. We have a stationary atmosphere. The direction of the air density gradient will be vertically and precisely from top to bottom (the density will increase downwards).

That is the meaning of the gradient.

This consequence is purely mathematical, it can be proved. What does the equation physically mean? What physical interpretation can we give it?

Consider a curve with direction. Here we have an electric field:

Take a point charge q   and we will move the charge along a given curve from point (1) to point (2). Since the charge is exerted by the force from the electric field, the work of the electric field as the charge moves along the curve   equals: The work that is done by the electric field when the charge moves, if I took and brought the charge from point (1) to point (2), and then brought it back (the circuit closed!). Then it follows that.

Work on the movement of charge in a closed loop is zero.

It means something else: what the work on moving the charge from point (1) to point (2) does not depend on the path of movement.

It may not be very obvious. So I crossed some path from (1) to (2), the field did some work, by the way, this work is positive. I will put the rails from point (1) to point (2). I'll put a trailer on them from a toy railway, put a charge in the trailer, and this trailer will travel (an excess of kinetic energy will transfer to the internal one). At point (2) I transfer the arrows and let the trailer along a different path. So the trailer will go, you can attach a turntable to it ... but it is known that the circulation is zero, and you cannot build a perpetual motion machine.

And now we have the following mathematical result:. An electrostatic field is a gradient field. This scalar function, whose gradient is the electric field strength, is called potential   electric field.

Not every vector field can be obtained as a potential gradient. The electrostatic field is represented by a single scalar function of the coordinates, rather than three, as one might think of by its vector character. Set one function of coordinates - and get a picture of the electric field.

Which one physical meaning   this scalar field?

And now let's do what we have under the integral. vector   - it is: , and the whole integrand there is a full differential.

Then, returning to the formula (*), we write:

We will come from point (1) to point (2), summing the change in potential. The moral is: here we have the starting point, transfer the charge to a point, here the value of the potential j() and work equals. Work on the movement of charge from one point to another is equal to the magnitude of the charge multiplied by the potential difference.

Now we have two descriptions of the electrostatic field. Either we set the tension, or we set the potential at each point. j. The words "potential difference" you should literally understand - this is a difference. Here is a synonym for potential difference, which is used in electrical engineering - voltage. This means that many of you are prone to use the words "voltage in the chain" did not know their meaning. This is synonymous with potential difference.

What do the words mean, that the voltage of a city network is 220 volts? There are two holes (potential difference between 220V holes), if you tear out the charge from one and walk with it, and then return it to another hole, then the field will be equal to V. A vivid example of a battery: you took a metal ball from the terminal the battery, put it in your pocket, went somewhere with it and then attached it to the second terminal, then the work will be like this: V.

Where we had voltage and potential difference, add this formula:.

Here is the point, here is the point, this curve, and the meaning is as follows: this formula is a universal iron recipe for finding the potential difference. If you ever come across a requirement or need to find a potential difference between two points, then the hand should automatically write this formula, and when we write it, then you can think. The words "potential difference" should simply cause this formula to be reflexive.

What are we talking about? What is the recipe? If you need to find the potential difference between one point and another, when the field strength in the whole space is set (field strength vector), the recipe: connect point 1 with point 2 of the curve and calculate this integral. The result does not depend on the choice of the path, well, and therefore it can always be chosen in the most reasonable way.

Well, for example, what does it mean reasonable sample? Let us assume that the field lines of force here are such radial curves:

And you need to find the potential here, point 1, well, let's say, point 2. How to choose a curve going from 1 to 2? The first thought, of course, is to take it like this: hold it along a ruler, calculate it from it. The idea is, of course, fast, but not very correct, because at all points of this curve the vector is alternating and directed at an angle to the line, and the angle is still changing - it is difficult to take the integral. But then, through point 2 you will spend a sphere and a path like this: along the radius - once, and then along this arc - two. Here is a reasonable curve choice. Why? Because here on this branch the vector is everywhere parallel to the line, the integral is immediately reduced simply to an ordinary integral, but on this branch the vector is everywhere perpendicular to the curve, and it does not make any contribution. Here is a reasonable choice of the curve for finding the potential difference.

Well, this is an example. If you imagine a specific type of field, then such a curve is easy to be, given that you have fields of arbitrary configuration that are complex will not come across, well, here we are in the process of occupying electrodynamics. Well, of course, if any such very arbitrary field is given, then there is no possibility to choose a curve in a special way, and then you need to attach a ruler there, but this is a mathematical problem, you can count it. All right, all right. The next item.

Fields created by charge distributions with good symmetry

Well, and immediately such a definition: with a sufficiently good symmetry, the field strength can be found from the equation. So, with a sufficiently good symmetry, the field can always be found from this integral theorem. Well, we have this first Maxwell equation. And now special cases.

1) Central (spherical) symmetry.   Let the charge density be. This means that the density, which, in general, is a function of the coordinates of a point, depends only on, that is, only on the distance to the origin of the coordinates, which means that the origin is the center of symmetry. This form = means that the density on any sphere of radius r   - a constant, some kind of density, well, and non-zero, on any sphere it is constant. This means that the distribution has spherical symmetry, and the field created by it will also have spherical symmetry. It follows that (potential as a function of a point) it is. From here equipotential surfaces - spheres centered at the origin, that is, here in any sphere potential is a constant. It further follows that the field lines of force, which are always orthogonal to the equipotential surfaces, the field lines of force are the following radial rays:

The design of the electric field can be only that. And now notice, there was no specificity of electricity here, all these conclusions were obtained only from considerations of symmetry. Any vector field would have such a structure, whatever physical nature it has. Only the power of symmetry considerations very often allows conclusions to be drawn without reference to a particular subject of conversation.

From here it follows that the field strength on any sphere can be represented as follows:. This radius vector divided by its own module is the unit vector in the direction of the radius vector. Everything. We write further this formula. As a closed surface, which appears in the integral (the flow is calculated on a closed surface), choose a sphere. We can take it (the surface) any, equality does not depend on it, but it is convenient to take. We write:. This equality is due to the fact that, is the unit vector in the direction of the radius vector (this is the normal vector to the sphere, but the normal to the sphere at this point coincides in direction with the radius vector of this point, these vectors are parallel), and the projection of the radius vector on himself is his module, of course. Further, at all points of the sphere is one and the same, we take out the integral sign: (this was all mathematics, it still had nothing to do with physics, and physics is the following equality), this value should be equal to the integral of the charge density over the volume of the sphere the flux is calculated (integral of density over volume, this is the total charge inside the sphere): where is the charge inside the sphere of radius. And this statement is true for a sphere of any radius. Hence the conclusion - with central symmetry, the field strength at all points of the sphere of radius is:

where is the unit vector of the normal to the sphere. This formula, one and only, finishes all the tasks of central symmetry. The only problem is to find the charge that is inside this sphere, well, this is not a very difficult problem.

We can continue this business a little bit. Due to the fact that in any sphere, the integral over the volume can be reduced, in principle, to a one-time integral, integrating over the ball layers, well, I will write here without detailed comments. This is the volume of the ball layer of radius thick. Why I put the touches here, of course. it is in the upper limit of the integral, well then, so as not to confuse the variable of integration with the upper limit, there I am writing instead. So, if this function is presented, then such an integral is calculated. So, everything with a central symmetry end. The second case.

2) Cylindrical symmetry. Enter the cylindrical coordinates, goes to. In our cylindrical coordinates, density is only a function of, that is, it does not depend on and does not depend on. This means that there is an infinite cylinder, and on the surface of a cylinder of any radius the charge density is constant, and the whole thing goes on ad infinitum, this is the situation. Immediately, of course, it is clear that this is not physically realized, but as some idealization, this is reasonable. Write again means equipotential surfaces   - These are cylinders with an axis that coincides with the axis of symmetry, that is, with the axis. And the lines of force lie in the planes orthogonal to the axis. So. As a closed surface, choose a cylindrical surface of radius and height, a cylindrical surface, closed by two lids so that it is closed. Normal is always taken out. For reasons of symmetry, it is clear (the field strength at any point of the cylindrical surface is directed along the vector, and the value depends only on the distance to the axis of symmetry). Since our surface is now defined in several pieces, the integral will be represented as the sum of the integrals over these pieces:.

The integral over the caps is zero, because the vector slides over the caps, the scalar product with the normal is zero. .

The inner filling of this cylinder is integral over. where is the charge per unit length of the cylinder of the radius, that is, it is the charge of the pellet of radius of unit thickness. From here we get the result:

field strength at all points of the cylindrical surface of the radius.

This formula kills all the problems associated with cylindrical symmetry. And finally, the third point.

3) A field created by a uniformly charged plane. Here we have a plane Yzcharged to infinity. This plane is charged with constant density s. s   called surface charge density. If you take an element of the surface, then it will charge. So, symmetry is such that when shifting along y   and z nothing changes, it means that the derivatives y   and z   from anything should be zero:. This means that potential is a function. x   only: Here is a consequence. This means that any plane is orthogonal to the axis. x   is an equipotential surface. On any such plane j= const. The lines of force are orthogonal to these planes, which means the lines of force are straight parallel to the axis x. It follows from symmetry considerations that if they go to the right of the plane here, then they should go to the left of the plane to the left (it is expected that there is a mirror symmetry).

The question, in fact, with mirror symmetry is not so simple. Here, before the not very long time, in my memory, it was believed that mirror symmetry, of course, takes place in nature, that there is no difference between left and right. But it was discovered in the 60s that in fact such symmetry is not fulfilled, nature distinguishes right from left. There will be another reason to talk about it. But here it is fulfilled for us.

Let be the unit vector along the axis x. As a closed surface, we take a cylinder cutting through a plane with two covers. The field strengths are shown in the figure.

The lateral surface integral is zero, because the lines of force slide along the lateral surface. But as the area of ​​the base of the cylinder. If the covers are taken at equal distances from the plane, then again due to symmetry is a function of the distance to the plane, then we will write this:. Then we have:, and this is the charge that sits inside our surface.

From here it turns out:. What we see is that the length of the cylinder, well, the distance from the covers to the plane, fell out of the formula, that is, at any distance from the plane, the field strength is the same. So the field is homogeneous. We finally write:

This formula automatically takes into account the sign of the charge: if. This formula gives an exhaustive description of the field of a charged plane. If there is not a plane, but an area of ​​finite thickness, then the field should be divided into thin plates and calculated.

Note, for a point charge, the field strength decreases with distance as it does; for a cylinder, as it does for a plane it does not decrease at all.

The last two cases are practically unrealizable. Then what's the point in these formulas? Such: for example, this formula is valid near the middle of a flat charged piece. Strictly such a formula (a uniform field fills the entire space) is not realized in any physical situation.

A field created by an arbitrary charge distribution.

Point charge field.

Let there be one point charge q. This is a special case of spherical symmetry. We have the formula:, where is the charge inside the radius sphere rbut if the charge is a point, then for a point charge, for any r. It is clear why, on any radius inside a sphere, a point remains a point. And for a point charge. This is a point charge field. Point charge field potential:.

Field of point charge system. The principle of superposition.

Suppose we have a system of charges, then the field strength created by the system of point charges is equal at any point to the sum of the strengths created by each of the charges. I could write immediately if you could read the formulas freely. Learn to read formulas narratively. Multiply the charge by the vector, and divide by the module of this vector, and what is the module of the vector is the length. This whole thing gives a vector directed along the vector.

The fact that the fields add up is not at all obvious. This is a consequence of the linearity of Maxwell's equations. Equations are linear in. This means that if you find two solutions, they add up. Are there any fields for which the superposition principle is not fulfilled? There are. The gravitational field is not in Newtonian theory, but in the correct one, does not satisfy the principle of superposition. The earth creates a certain intensity at a certain point. The moon too. They put the Earth and the Moon, the tension at the point is not equal to the sum of the tensions. The field equation is not linear, physically, this means that the gravitational field is itself a source. So. It's all over.

Last time we stopped to discuss the field created by the system of charges. And we have seen that the fields created by each charge separately at a given point are added. At the same time, I stressed that this is not the most obvious thing - this is a property of electromagnetic interaction. Physically, it is connected with the fact that the field is not a source for itself; formally, this is a consequence of the fact that the equations are linear. There are examples of physical fields that are themselves a source. That is, if in some volume this field is, so it creates the field itself in the surrounding space, formally, this is manifested in the fact that the equations are not linear. There I wrote a formula for tension, we will write another formula for potential.

Potential point charge system.

There is a charge system, etc. And then for some point we write the following formula:. So, here is a recipe for potential. Tension is equal to the sum of the tensions, the potential is equal to the sum of the potentials.

Comment. It is almost always more convenient to calculate the potential rather than intensity, for obvious reasons: intensity is a vector, and vectors must be added according to the rule of addition of vectors, well, the parallelogram rule is, of course, more boring than adding numbers, potential is a scalar value . Therefore, almost always, when we have a fairly dense distribution of charge, we look for potential, the field strength is then found by the formula:.)

Field created by an arbitrary limited charge distribution).

Well, what does the epithet "limited" mean here? The fact that the charge is localized in a finite region of space, that is, we can cover this charge with a closed surface such that there is no charge outside this surface. It is clear that from the point of view of physics, this is not a limitation, well, indeed, we are almost always dealing only with limited distributions, there is no such situation that the charge is spread throughout the universe, it is concentrated in certain areas.

This is the problem: the area is occupied by a charge, an electric charge is spread over this area, we must fully characterize this charge and find the field created by it. What does it mean to fully characterize the charge distribution? Take the volume element, the position of this element is given by the radius-vector, in this element there is a charge. In order to find the field, we need to know the charge of each volume element, which means that we need to know the charge density at each point. This function has been presented; for our purpose, it exhaustively characterizes the charge distribution, we don’t need to know anything else.

Let us be interested in the field at the point. And then the principle of superposition. We can take charge dqwhich sits in this volume element, dotted). We can immediately write an expression for the potential that this element creates at this point: this is the potential created by the element at the point. And now it is clear that we will find the full potential at this point by summing over all the elements. Well, let's write this sum as an integral:.)

This recipe is triggered by iron for any charge distribution presented, there are no problems other than the calculation of the integral, but the computer will calculate this amount. The field strength is:. When the integral is calculated, the tension is simply differentiation.

A field at a great distance from a limited charge distribution.

At the same time we will get acquainted with the standard method of obtaining approximate solutions. The problem is again. We have a charge distribution), we will now try to get a more accurate formula, not so radical, but, if you go far enough, but still, when this distribution does not look very pointed, we want to get a more accurate approximation. Let us L   - the characteristic linear size of the system, we will assume that, it can be arranged differently:, it is within the distribution, it is a small quantity.

And now what we do:.

Standard trick: when you have a sum in which one item is large and the other small, then it always makes sense to put a big item out of the bracket and get a total of one plus some small additives that decompose in a row.

Then for the field strength we get:

Dipole field.

A dipole is a charge distribution for which the total charge is zero, but the dipole moment is not zero:. It is easy to present such a distribution. Suppose we have two identical point charges, but opposite signs. . The dipole moment here was determined:. what does that mean? charge in a small volume element dq   multiplied by the radius vector and summed over all charges, if you write this thing through the sum, it will be like this:. This integral, if we imagine all this as a set of point charges, is represented by such a sum, each charge is multiplied by its own radius vector and everything is added.

By the way, in mechanics, if we took the particle mass, multiplied by the radius vector and summed, so that we get? We would get the mass of the system multiplied by the radius-vector of the center of mass. If the origin of coordinates was chosen in the center of mass of the system, then the “dipole moment-mass distribution” would always be equal to zero. Electric charge has different signs, here the situation is different.

So, the dipole moment for our system is:. The dipole moment of two charges of the same magnitude and opposite in sign is a vector going from a negative charge to a positive one multiplied by the charge.

Now we find the electric field. Let the dipole moment, vector, at the origin of coordinates be oriented along the axis OH. Calculate the field at ( x,0,0).

The moral is: on the axis OH   field strength decreases as, that is, it is inversely proportional to the cube of the distance, from a point charge - inversely proportional to the square of the distance. The direction of the vector at ( x, 0,0) is determined by the direction of the vector, that is, the intensity is directed along the axis OH.

Now take a point (0, at, 0). . What does that mean? What for this dipole is the vector at ( x, 0,0) such, and here at the point (0, at, 0) vector - and two times smaller, at the same distance, x=at.

  An electric dipole oriented in this way creates a field with such lines of force:

This is the structure of the dipole field.

Many molecules possess a dipole moment, and properties of a substance are related to this, which we will consider next time.

Force acting on limited

charge distribution in external field

The problem is this: we have a field, we have some kind of charge, spread over a certain area, localized charge). We are interested in what force will act on a charged body, well, or ultimately, how it will move, being in an external electric field.

You must, of course, imagine that if this limited distribution is a point charge, then you know what kind of force acts on it). Our task is to find the force acting on an arbitrary charge distribution.

Well, in general, it is clear how this can be done, it is necessary to divide the distribution into a set of point charges, find the forces acting on each of these charges, and then add up all the forces across the distribution. Here is a program. Well, how it is implemented, we will now see.

The point charge acts strength   where it turns out potential charge energy   in the electric field (we saw in mechanics that if the force is represented as a gradient from some scalar function, then this function is interpreted as potential energy), and the law of conservation of energy takes place, and the charge moves like this:, this is called the total energy ( the sum of kinetic and potential energy). This is for point charge.

The potential energy of a limited charge distribution in an external field.

Suppose there is a charge distribution, we divide the charge into small volume elements dV, in this element of the volume of charge. is the potential energy of a charge in a volume element dV, the energy of the elementary charge. Then all potential energy of this distribution will be equal.

This is the exact formula. Now we will get an approximate formula.

Select some point inside the distribution, the radius vector of this point will be, the radius vector is the vector going from the selected point to this volume element,. Then the potential at the point is). For the time being, the decomposition is written to the accuracy of the first derivatives, then the terms with the second derivatives will go there, and so on, this is a mathematical fact.

The basis of this calculation is the following assumption: we assume that the potential varies little within the limits of the distribution, that is, the distribution is not too large. This means that the second term is much smaller than the first, that is, the value of the potential at some point inside is such and such, and the addition to the potential, when we reach the distribution edge, is small, so further we throw out the terms. We now substitute this matter into the formula for potential energy:).

We have extracted just such a nice formula:, where is the radius vector going to a certain point inside the distribution, this is again decomposition into multipoles.

What does this physically mean? The main contribution to the potential energy is the total charge on the potential value somewhere inside the distribution, the correction term taking into account the dipole moment of the distribution (the dipole moment characterizes how the negative and positive charges are placed relative to each other), and other characteristics that take into account moments of higher orders .

And now we can find force (force is a gradient of potential energy), we write:. And finally we get the following result:

The force acting on a dipole in an external field

Let be q= 0, but. Then the force is equal. Where can this appear in physics? Very many bodies are electrically neutral, that is, they have no charge, but have a non-zero dipole moment. The simplest object of this kind is the molecule. A molecule is an entity in which the positive and negative charges add up to zero in total, but do not coincide in space. Such a system has a dipole moment on which a force acts.

By the way, it is easy to understand why there is a force acting on a dipole. Let's say a field is created by a positive charge, we have a dipole, a system consisting of a negative charge -q   and positive + q. The resulting force is: If you apply a formula to this situation, you will see that it will give the correct result.

  The moment of force acting on a dipole in an external field

Suppose we have a uniform electric field and a dipole, which we represent as two point charges. On charge + q   force acts on charge -q   - strength. If the field is homogeneous, then these forces together will give zero, but the moment is not equal to zero. Two such forces create a torque, the vector of this moment is directed perpendicular to the plane of the figure. Such a moment acts on an electrically dipole in a uniform field, this moment of forces tends to turn the dipole so that its dipole moment becomes parallel to the vector.

This is what it means: if a dipole field is placed in an electric field, as shown in the figure. 5.5 , the moment will turn it so that the dipole becomes parallel, and the force will pull it further into the electric field.

Now we can understand how a substance will behave in an electrostatic field.

Substance in electrostatic field

From the point of view of electricity, the substance is divided into conductors and dielectrics). Guides - These are bodies in which there are free charge carriers, that is, charged particles that can move freely inside this body (for example, electrons in a metal, ions in a liquid or gas ). Dielectrics- These are bodies in which there are no free charge carriers, that is, there are no charged particles that could move within this dielectric. The behavior of these bodies in the electric field is different, and now we will consider these differences.

Dielectrics in an electric field

Dielectrics are bodies composed of neutral molecules. Molecules are polar (possessing a dipole moment) and non-polar (not possessing a dipole moment). A dielectric consisting of polar molecules is polarized in an external field., that is, it will acquire a dipole moment due to the preferential orientation of molecular dipoles in the direction of the external field.

Here we have a piece of dielectric, the external field is absent. The dipole moments of the molecules are randomly oriented, and on average, the dipole moment of any volume element is zero ( fig.5.6).

However, if we place an external electric field, a preferential orientation will appear, all these dipole moments will orient in approximately the manner shown in the figure. 5.7 . They will not be able to build everything along the field, because the chaotic thermal movement destroys the structure, but at least against the background of this chaos they will all strive to orient themselves along the field.

A dielectric consisting of non-polar molecules is also polarized., because these molecules acquire a dipole moment in the external field.

However, if we introduce this molecule into an external electric field, then the external field pulls away the positive and negative charges, and the molecule acquires a dipole moment.

The polarization of the dielectric is characterized by a vector. The meaning of this vector is as follows: if we take the element of volume dV, then the dipole moment of this volume will be equal. The value of the dipole moment of a small volume of the dielectric is proportional to the volume of the element, and the coefficient is a vector, in short, is the density of the dipole moment.

Now a little math. We have a fundamental equation (the first Maxwell equation, which connects the electric field with a charge). From this integral law follows a differential one:, this is by the Ostrogradsky-Gauss theorem.

There is such a wonderful mathematical theorem for an arbitrary vector field.

The meaning of this theorem is: we have a vector field, we have a closed surface, we calculate the vector at each point of the surface, multiply by the normal, by the area of ​​the small surface and sum up, this integral depends, of course, on the behavior on the surface, we get a number, now the vector field leads somehow we are inside this surface, at every point inside we calculate this very divergence, we get a number, integrate over the volume, we get equality. The behavior of the vector on the surface, it turns out, is connected with the filling of this volume. I leave the vector on the surface as before, and inside I can deform this field, but no matter how the field inside is deformed, the integral will not change (although at each point the divergence will change).

It is here that such a sly connection between the behavior of the vector field on the surface and its behavior inside the volume is in effect

Equality is obtained as a consequence of the Ostrogradsky-Gauss theorem. Here on the right is the charge density, which means that the divergence of tension is equal to the charge density. The dielectric polarization is equivalent to the appearance of a charge with a density   . This is not very obvious. If the polarization vector is constant, then no charge appears in the volume. Now, if the vector changes from point to point, then this is manifested in the fact that a certain fictitious charge appears in this volume element.

Taking into account this matter, the equation will be rewritten in the form where is the density of the real charges, and is the density of the associated charges, here are the fictitious charges resulting from the polarization of the dielectric. Now we can transform this equation. Multiply everything by and move the value to the left, we get the following equation:, where is the density of the real charges, or. Vector is called electric field induction, and for this induction we have obtained such a wonderful equation:.

And from it we now with the help of the Gauss theorem return to the integral equation:. For homogeneous dielectrics, a linear function of the field strength (), in general, for an arbitrary dielectric, is a certain function of the field strength (). We write then, where the coefficient called dielectric susceptibility. Hence, this coefficient characterizes the tendency of the dielectric to polarization. Returning to the expression for, we get for a homogeneous dielectric:. Magnitude is called medium dielectric constant. This is a dimensionless quantity, greater than one. Then the relationship between and:

Example. Suppose we have a charged ball with charge + Qplaced in a homogeneous infinite environment with dielectric constant. What field will exist inside this dielectric?

We proceed from the equation. Surround this charge with a radius sphere r. The vector should be directed along the radius, this is a consequence of spherical symmetry. , from here we get:; .

Moral: when we solved such a problem for emptiness, the field strength was equal, when the ball was placed in a dielectric, the field strength was less than in a vacuum. It is easy to see why this happens. When a charge is placed in a dielectric, due to the polarization of the dielectric, the charge + Q   enveloped by a negative charge -q ’which acts on the surface of the ball.

The resulting charge is less than QHowever, significantly, the induction is determined only by the real charge. The charge appearing on the dielectric does not affect the induction (this vector was specifically introduced in this way). The intensity of the field is affected by all charges, including -q ’.

Electrostatic conductors

Conductors are bodies in which there are free charge carriers, that is, charged particles that can move freely within this body. Well, usually, the word conductor is used, then the word metal is used as a synonym, the metals are remarkable because they contain free electrons. But, in fact, the concept of the conductor is wider. Water, for example, is a conductor; pure water itself is not H 2 O, it consists of neutral molecules, and there are no free particles there, but salt, that is, iodine, is usually present in dissolved form in water, and due to this almost all water is a conductor.

By the way, already due to the fact that we considered dielectrics last time. The dielectric constant of water is very high compared to such pure water, therefore, water is a very effective solvent for many substances, say, for solids, which are arranged according to the ionic scheme. So, if molecules are bonded in a solid due to the Coulomb interaction (say, one atom gains an electron, the other loses, these atoms are connected by Coulomb forces), then water destroys such bonds very effectively due to its high dielectric constant. Positive and negative charges are enveloped. bound chargesand these connections are destroyed. Water in this regard is a very good solvent.

Water, in general, is a wonderful substance. All bodies shrink when cooled, that is, the density increases (when cooled, the density increases, decreases when heated). Here there is an anomalous phenomenon in this: the maximum density of water at +4 О С, at a temperature below +4 О С the density drops again, that is, a further drop in temperature leads to a drop in density, that is, to the expansion of water. This amazing behavior is related to the fact that water plays such a prominent role in our life: firstly, a good solvent for various mineral salts, and secondly, this is the anomalous density behavior. If this were not, then, for example, in reservoirs, lakes, rivers, there would be no life, the reservoirs would freeze to the bottom, and the reservoirs would not freeze through. Well, why are they freezing? The upper layer of water cools down and goes down because it has more density, the warm layers from the bottom are pushed up and cooled again. And this cooling would go very efficiently. In fact, this is not happening. When the temperature of the lower layers is +4 ° C, they acquire maximum density and do not float. Cooling can go only due to thermal conductivity, not due to mass transfer, but due to thermal conductivity. Thermal conductivity is a slow process, and, say, over the winter, the reservoir does not have time to freeze, but if the water density did not behave this way, it would freeze to the bottom and, in the end, everything that lives there would give ends , and so in this water +4 О С lives.

Some statements:

1. Intensity inside conductor is zero   (this is in an electrostatic field). For good reason. If there was a field, then the charge e   an equal force would act, and under the action of this force the charges inside the conductor would move (the electrons in the metal would move). How long can they move? It is clear that they cannot move forever, well, let's say, we have a piece of iron in it, and in it they move, move and move, the iron heats at the same time, and nothing happens around. That, of course, would be ridiculous. And the following happens: we have a conductor and an external electrostatic field is turned on, the charges begin to move, while the charges inside move so that their own field completely extinguishes the external applied field, and the process stops. This movement with conventional measurements almost instantly. The value of the electric field inside the conductor is zero. Hence the consequence

2. The potential inside the conductor is constant. Well, obviously, the intensity is the potential gradient, the derivative of the potential, if the intensity is zero (this means that the derivative is zero), the function itself is constant. The potential at all points of the conductor is the same. This statement is true for all points of the conductor up to the surface. Hence the moral:

3. The conductor surface is an equipotential surface.. Well, and from here:

4. The field lines are orthogonal to the conductor surface..

  All this can be summarized as follows:

Let's say we have a point charge and a conductor introduced into the field of this charge. The following will occur: where the lines of force enter, the negative charge will concentrate on the surface of the conductor, say, electrons will fit here, and positive charges will appear on the opposite side, these are not compensated charges of the ions from which the crystal lattice is built.

The field lines of force will be orthogonal to the conductor, on the other hand they will come, again orthogonally to the surface of the conductor. Well, and, in general, the electric field will be significantly changed. We see that if the conductor surface is brought into the charge field, the entire field configuration will be distorted. If you put a charge on the conductor (or remove some of the electrons from it, or implant), this charge will be distributed so that the intensity inside is zero and that the surface of the conductor takes the same potential at all points.

This thing is useful to keep in mind, then you can qualitatively imagine what the field looks like in the vicinity of a charged conductor.

I will draw an arbitrary conductor and put a charge on it + qWell, a solitary guide (nothing else). What will be the structure of the field? Considerations are as follows: the surface is equipotential, the potential changes continuously, which means that the neighboring equipotential will differ little from this. Here, I can draw a system of equipotential surfaces more or less qualitatively. Then they will be so straightened, and, in the end, at large distances the orbits will be spheres, as from a point charge. And now, the field lines are orthogonal to these surfaces ...

Here is a hedgehog turned out. Here is a picture of the lines of force.

Now a little math.

We have an equation. In the void, given that, we get the following equation:). The potential of the electric field in a vacuum satisfies the equation, which is called the Laplace equation.

Mathematically, this problem is reduced to solving such an equation under given boundary conditions, which is on a given surface).

Capacitors

Suppose we have a separate conductor, on which the charge is planted qThis conductor creates a field of the configuration shown in the figure. 6.2 . The potential of this conductor is the same in all currents, so you can simply say the potential of the conductor, and, in fact, the word potential requires specifying the point at which this potential is determined. It can be shown that the potential of a solitary conductor is a linear function of the charge that is planted on it, double the charge, the potential will double. This is not an obvious thing, and I cannot bring any arguments on my fingers to clarify this dependence. It turns out that the field structure does not change, well, the pattern of lines of force does not change, the field strengths at all points grow in proportion to this charge, but the overall picture does not change. I repeat once again - not an obvious thing. Well, okay, the potential of a solitary conductor is a linear function of charge,. We write then, introducing the coefficient of proportionality in this way, where this coefficient of proportionality WITH   is determined by the geometry of the conductor and is called capacity of solitary conductor). The capacity of the conductor is not its property, that is, it is impossible to write “such-and-such capacity” on some piece of iron, because the presence or absence of foreign bodies near changes this capacity. Its capacity, the coefficient of proportionality, the capacity of a separate conductor is not a property of this conductor, it still depends, besides it, on the presence or absence of other bodies. However, there are devices that are called capacitors, special devices for which the concept of capacity has an unambiguous meaning.

A capacitor, generally speaking, is a system of two conductors, one of which completely covers the other, that is, ideally, a capacitor is such a thing:

If the internal conductor charge + q, and on the outside -q. Inside there is an electric field of such a configuration (the lines of force are orthogonal to the surfaces). And no external charges affect this field, external fields do not penetrate into the conductive cavity, that is, an electrostatic field can be shielded. If you want to live without an electric field, here, climb into the iron barrel, close the lid and everything, it will not penetrate you there, say, the transistor will not work there in your hands in this barrel, electromagnetic waves will not penetrate there. Why by the way? But because the field inside the conductor is zero, since the intensity is related to the charge distribution on the surface, and the conductor's filling is no longer involved there, you can throw out this stuffing, get a cavity, nothing will change. Inside the conductor, the field is determined only by the configuration of these conductors and does not depend on external charges, then, if there is a potential on the internal conductor, and on the external conductor, then we will again have such a thing that the internal energy is proportional to the charge: qthat sits on the picture inside the conductor. Then we write:. Such a device is called a capacitor, and WITH   called capacitor capacitance. This is already a property of the device, you can write on it: “Capacity WITH". A capacitor is a common element in electricity, in electrical engineering and in radio engineering, and “capacitance such and such” is directly written on them, and this quantity does not depend on what is around. Dimensional capacity of what is it? , the capacity in one farad is the capacity of such a device, that if you put a charge of 1 K on it (this is a huge charge), then the potential difference will be 1B. There are no such capacitors on earth, on Earth it is simply impossible to build such a capacitor that it has a capacity in the farad, therefore, going to this capacity, we will use microfarads.

Capacitor energy

Conventionally, two conductors represent a capacitor. How can I put a charge on these conductors, well, charge the capacitor? So, for example: we take a charge and transfer it from one conductor to another, for example, from one we remove several electrons and drag it to another, this is the process of charging a capacitor. How is this actually done, how can you drag electrons from one conductor to another? We have two conductors, the source is connected, the battery, the key is locked, the battery begins to move the charges from one conductor to another. Until then, we will be able to distill them is a separate issue, we will consider it in due time, but now it is simple: inside this battery there are forces, external forces in relation to electrostatics, and these forces distill charges from one conductor to another. It is clear that in order to make this division, it is necessary to expend some work. That's why: we removed the electron, a positive charge appeared, and this electron begins to be attracted to the positive charge, we need to do work to pull it away from this charge. This work can be counted. Suppose we have two conductors with potentials and, we transfer the charge, while doing the work, equal. We now take into account that the potential difference is a function of the charge:, then the work, and the full work will be. If we achieve that on each conductor becomes a charge equal in magnitude qthen such work is done. The question is, where does this work go? Stored in the form of energy of the capacitor, and it can be obtained back. Capacitor energy is:. By the way, this explains the word capacitor (storage): on the one hand, it is a charge drive, on the other hand, it is an energy storage device, and capacitors are really used as energy storage devices. If the capacitor is discharged, this energy is released. By the way, high-capacity capacitors (structures of the order of this audience) are discharged with a terrible thunder when closing, this is a dramatic process.

Electrostatic field energy

The problem is this: a charged capacitor has energy, where is this energy localized, with what is it connected? Energy is an integral characteristic, just a device has such energy, the question, I repeat, is the localization of energy, that is, what is the energy of what? The answer is this: the energy of a capacitor is, in fact, the energy of an electrostatic field, the energy belongs to the field, neither the plates of the capacitor, nor the charge. We will continue to get a clear theorem for the energy of the electromagnetic field, and now some simple considerations.

Flat capacitor. Here is a device called a flat capacitor, well known to everyone:

This means that the distance between the plates is much smaller than the characteristic linear size, S   - plate area. The plates have a large area, the gap is small, in this case the field lines of force are homogeneous and external charges do not affect it. The field strength is where. We know the formula for the plate with the surface density:, between the plates, the fields are folded, destroyed outside. Since the field is uniform, the potential difference equals:, where d   - the distance between the plates. Then we get that. Indeed, they found that the potential difference between the plates is a linear function of charge, this is a particular confirmation of the general rule. And the coefficient of proportionality is related to the capacity:. If the capacitor volume is filled with dielectric filling, then there will be a more general formula:).

Now let's take a formula for the energy of a capacitor:. This formula is always valid. For a flat capacitor, we get:, where V   - is the volume of the area between the plates. In the presence of a dielectric, the energy of a flat capacitor is equal to:. The field strength inside a flat capacitor at all points is the same, energy is proportional to volume, and this thing then acts as an energy density, energy per unit volume inside the capacitor. I repeat, further we will see good proof, this is so far as a suggestive consideration, but the situation is as follows. The electrostatic field has energy, and if we take a volume element dV, and inside this element the field strength equals E, then inside this volume will contain energy, determined by the field strength at a point inside this element. In any finite volume V   will contain energy equal.

What does it mean? Literally that's what. Now in this audience there is an electrostatic field, due to the fact that the Earth has a certain charge, and a charge of the opposite sign in the atmosphere, this field is uniform, I have already mentioned, for sure, the intensity is this: at the points where I have now prodded, the potential difference is of the order 100V, that is, the strength of this field is about 100V / m. This means that this audience has energy calculated by this formula: it is spread over the whole space, energy belongs to an electric field. Can I use it? Here the subtlety is, say, I came with a suitcase, put the suitcase here, opened it, then closed it, there is an electric field in the volume of the suitcase and, accordingly, energy. I took the suitcase and left, did I take away this energy? No, because I took the suitcase, and the field as it was here, remains. However, is it possible to extract this energy somehow? Yes. It is necessary to make the energy disappear in this volume, say, the electric field disappears in the volume of this audience, and then this energy will be released, if we destroy the field, then the energy will be released.

The procedure, for example, is this: here there is a uniform field, I take a metal plate and push it into this field perpendicular to the lines of force, the work is not performed and nothing happens; I push another plate in the same way, nothing happens either, well, the truth is, the field disappears inside the conducting plate, the charges protrude on the surface, but this is nonsense. And now I take the conductor to one plate, the key and the conductor to another, also an innocent affair, nothing happens at the same time. And when I close the key, what happens? These two plates are connected, it is one conductor, this means that their potentials must be equalized. Initially, there was potential on one conductor, on the other, and the potential difference was equal to where d   - this is the distance between the plates, and when I connect them with a conductor =, how can this be? The field between the plates disappears, because the potential difference is an integral. When I short-circuit them with a conductor, this configuration is obtained:

  How much is this process implemented? What is lightning and thunder? We have the earth, we have a cloud (these are capacitor plates), between them there is an electric field:

What is lightning? Breakdown, it is a diversion, it closes itself. Discharge occurs, the field disappears between the cloud and the ground. Thunder, what is it? Energy release of this field. All this thunder, crash and lightning is the release of energy between the cloud and the earth.

Capacitor energy is this. Of course, to take this integral, you need to know the whole field in the whole space, and how does such a simple formula result? Capacity, in fact, is an integral characteristic, in order to find the capacity of a system of charges, you need to know the field in all space. The whole difficulty of calculating the integral is equivalent to the difficulty of calculating the capacity.

Stationary magnetic fields

Let me remind you how we mined electrostatics. We have four Maxwell equations in which all the electricity sits. We laid there, got electrostatics. We will now weaken these imposed conditions, we will now put, but we will get a stationary magnetic field. That is, over time, nothing changes, but the current density is associated with the movement of the charge. The charges move, but stationary, move so that at any point in space with time nothing changes. An illustrative example: a river flows, the masses of water move, but the flow is stationary, the water velocity at each point is the same. When the wind blows here and there in gusts, it is not a steady flow, and if the wind blows without gusts: everything whistles in the ears, and nothing changes with time, then this is an example of a steady flow.

The equations of electrostatics (the first and second Maxwell equations) remain unchanged, and the third and fourth will be:

Stationary means unchanging with time. Well, we will discuss the properties of this field next time.

We study the stationary magnetic field. Let me remind the original positions: that is, the charges move, but stationary. This field will be described by two equations (the third and fourth Maxwell equations):

Which means third equation? That the flow of a vector through any closed surface is zero, wherever this surface is taken and whatever shape it has. This means that the contributions to the flow are alternating, that is, somewhere the vector is directed inward to the surface, and somewhere outward. Formally, from equality 3. it can be shown that how many lines come out of the surface, so much does it enter it. Otherwise, no line of force ends inside a closed surface and no one begins. How can it be? It can only be this way: all lines of force are closed. In short, from the third equation it follows that magnetic field lines of force closed. That is, the power line can somehow go, go, but it will definitely come back and bite itself by the tail.

For the electric field, we had such a thing:. On the left, the design is the same, but on the right was the charge inside the surface. Hence the consequences: 1) the lines of force are closed and 2) there are no magnetic charges, that is, there are no such particles from which they would come out in this way (see fig.7.1a) induction lines, such particles are called magnetic monopoles.

  Magnetic monopoles are absent. This is a special problem of physics. Physics, following nature, which it reflects, loves symmetry, and Maxwell's equations have symmetry, but limitedly, in particular, for the intensity on the right is the sum of charges, for magnetic induction there would be the sum of magnetic monopoles. This is a violation of symmetry annoying, I repeat, nature loves symmetry. There were attempts about twenty years ago to discover monopoles, so it seems, for reasons of symmetry, they should be, but they did not. Theory had to look for reasons why they are not. The considerations of symmetry are so powerful that its violations require some explanation. Well, there are different hypotheses in which these monopoles appear, but why we don’t find them here are also different explanations, to the extent that in the early stages of the Universe, they were simply turned out to be pushed out of the space around us. In general, there are theories in which they appear, and within the framework of those theories, explanations are being sought why we do not find them on Earth. While we, referring to the fact that they are not detected, we write here zero and deal only with closed lines of force.

Now we turn to the fourth equation. We read it: take a closed loop, set the direction of the detour (the detour and the normal should form the right screw), at each point we define, we take the scalar product, we get the number, for all the elements we find these scalar products, we get the circulation along the contour, this is some number. The equation states that if this circulation is non-zero, then the right-hand side is non-zero. And here what? The current density is associated with moving charges, the scalar product is the charge that slips through this area per unit of time. If the circulation around the contour is non-zero, then this means that some charges cross the surface stretched over this contour. This is the meaning of the fourth equation.

Then we can draw the following conclusion: the magnetic field lines are closed, take as a contour some magnetic field line along this line, because the product does not change sign. This means that if I take the surface S, stretched on the magnetic field line, then, of course, this surface is crossed by the charges in this way:

It can be said that the magnetic field line always covers the current, in other words, it looks like this: if we have a conductor through which current Á flows, for any circuit that covers the conductor with current,; if there are several conductors, again I will take the contour, the surface stretched on it, two conductors pierce it, then, taking into account the signs: the current Á 1 is positive, Á 2 is negative. We have then. This is immediately the general such properties of the magnetic field and current. Hence, the power line always covers the current.

Magnetic field of an infinite direct conductor with current

Let along the axis Oz   there is an infinitely long conductor through which a current with a force of Á flows. And what is the current strength? , is the charge that crosses the surface S in time. The system has axial symmetry. If we enter cylindrical coordinates r,   jzthen cylindrical symmetry means that and, moreover, when offset along the axis Ozwe see the same thing. That is the source. The magnetic field must be such that these conditions and are satisfied. This means that: the magnetic field lines are circles lying in the plane orthogonal to the conductor. This immediately allows you to find the magnetic field.

Let us have this conductor.

Here is the orthogonal plane

here's a circle of radius r,

i'll take a tangent vector here, a vector directed along jtangent to a circle.

Then where.

As a closed loop, choose a circle of radius r = const. We write then, the sum of the lengths along the whole circle (and the integral is nothing but the sum) is the length of the circle. where Á is the current in the conductor. On the right is the charge that crosses the surface per unit of time. Hence the moral:. So, the direct conductor creates a magnetic field with lines of force in the form of circles covering the conductor, and this value AT   decreases as it moves away from the conductor, well, and tends to infinity if we approach the conductor when the contour goes inside the conductor.

This result is only for the case when the circuit covers the current. It is clear that the infinite explorer is unrealizable. The length of the conductor is an observable quantity, and no observable quantity can take infinite values, not such a ruler that would allow to measure infinite length. This is an unrealizable thing, then what is the use of this formula? The sense is simple. For any conductor, the following will be true: the magnetic field lines of force are close enough to the conductor — such are closed circles covering the conductor and at a distance ( R   - radius of curvature of the conductor), this formula will be valid.

The magnetic field created by an arbitrary conductor with a current.

The law of Bio-Savara.

Suppose we have an arbitrary conductor with current, and we are interested in the magnetic field created by a piece of this conductor at a given point. How, by the way, did we find in the electrostatics the electric field created by some kind of charge distribution? The distribution was divided into small elements and the field from each element was calculated at each point (according to the Coulomb's law) and summed up. The same program here. The structure of the magnetic field is more complicated than the electrostatic, by the way, it is not potentially, a closed magnetic field can not be represented as a gradient of a scalar function, it has a different structure, but the idea is the same. We break the conductor into small elements. So I took a small element, the position of this element is determined by the radius-vector, and the observation point is determined by the radius-vector. It is claimed that this element of the conductor will create an induction at this point according to this recipe:. Where does this recipe come from? It was found experimentally at one time; it is difficult for me, by the way, to imagine how it could be experimentally found such a rather complex formula with a vector product. In fact, this is a consequence of the fourth Maxwell equation. Then the field created by the whole conductor:, or, we can now write the integral:. It is clear that calculating such an integral for an arbitrary explorer is not a very pleasant exercise, but as a sum it is a normal task for a computer.

Example.   The magnetic field of a circular coil with current.

  Let in the plane Yz   there is a wire coil of radius R through which the current of force Á flows. We are interested in the magnetic field that creates the current. The lines of force near the turn are:

The overall picture of the lines of force is also visible ( fig.7.10).

In theory, we would be interested in the field, but in elementary functions it is impossible to specify the field of this coil. You can only find on the axis of symmetry. We are looking for a field in points ( x,0,0).

The direction of the vector is determined by the vector product. The vector has two components: and. When we start to sum these vectors, then all perpendicular components in the sum will give zero. . And now we write:, =, a. and finally.

We produced the following result:

And now, as a test, the field in the center of the loop is equal to:.

The field of a long solenoid.

A solenoid is a coil on which a conductor is wound.

The magnetic field from the turns develops, and it is not difficult to guess that the structure of the field lines of force is as follows: they go thick inside, and rarely further. That is, for a long solenoid, outside we will assume = 0, and inside the solenoid = const. Inside a long solenoid, well, in a neighborhood. For example, its middle, the magnetic field is almost uniform, and outside the solenoid this field is small. Then we can find this magnetic field inside as follows: here I take such a circuit ( fig.7.13), and now we write:.

This is a full charge. This surface pierce the coils

(full charge) = (number of turns piercing this surface).

We will get this equality from our law:, or

The field is at a great distance from the limited current distribution.

Magnetic moment

This means that currents flow in a limited area of ​​space, then there is a simple recipe for finding the magnetic field that creates this limited distribution. Well, by the way, any source falls under this concept limited space, therefore there is no narrowing here.

If the characteristic size of the system, then. Let me remind you that we solved a similar problem for the electric field created by a limited charge distribution, and there the concept of a dipole moment, and higher order moments, appeared. I will not solve this problem here.

  By analogy (as was done in electrostatics) it can be shown that the magnetic field from a limited distribution at large distances is similar to the electric field of a dipole. That is, the structure of this field is as follows:

The distribution is characterized by a magnetic moment. Magnetic moment   where is the current density or, if we consider that we are dealing with moving charged particles, then we can express this formula for a continuous medium in terms of particle charges in the following way:. What does this amount express? I repeat, the current distribution is created by the fact that these charged particles move. Radius vector i-th particle vector multiplied by speed i-th particle and it all multiplies by the charge of this ith particles.

This design, by the way, we had in mechanics. If instead of a charge without a multiplier we write the mass of a particle, then what will it represent? The moment of the impulse system.

If we have particles of the same kind (for example, electrons), then we can write. So, if the current is created by particles of the same kind, then the magnetic moment is simply associated with the angular momentum of this system of particles.

A magnetic fieldcreated by this magnetic moment is equal to:

(8.1 )

The magnetic moment of the coil with current

Suppose we have a coil and a current of force I flows through it. The vector is different from zero within the loop. Take an element of this coil, where S   Is the cross section of the coil, and is the unit tangent vector. Then the magnetic moment is defined as:. What is it? This is a vector directed along the normal vector to the turn plane. And the vector product of two vectors is the doubled area of ​​the triangle built on these vectors. If a dS   - the area of ​​the triangle built on the vectors and, then. Then we write the magnetic moment equals. So

(magnetic moment of a coil with current) = (current strength) (coil area) (normal to a coil).

And now we have the formula ( 8.1 ) is applicable for the current loop and is comparable to what we extracted last time, just to test the formula, since I blinded this formula by analogy.

Suppose we have a coil of arbitrary shape at the origin of coordinates, through which the current of force Á flows, then the field is at a point at a distance x   equals: (). For round coil,. In the last lecture, we found the magnetic field of a round coil with a current, with these formulas coinciding.

At large distances from any current distribution, the magnetic field is found by the formula ( 8.1 ), and all this distribution is characterized by one vector, which is called the magnetic moment. By the way, the simplest source of the magnetic field is the magnetic moment. For an electric field, the simplest source is a monopole; for an electric field, the next in complexity is an electric dipole; for a magnetic field, everything starts from this dipole or magnetic moment. This, I once again draw attention, insofar as there are no these monopoles. If there was a monopole, then everything would be as in an electric field. And since we have the simplest source of a magnetic field, it is a magnetic moment, an analogue of an electric dipole. A good example of a magnetic moment is a permanent magnet. A permanent magnet has a magnetic moment, and at a great distance its field has the following structure:

The force acting on a conductor with a current in a magnetic field

We have seen that an equal force acts on a charged particle. The current in the conductor is the result of the movement of charged particles of the body, that is, there is no uniformly spread charge in space, the charge is localized in each particle. Current density On i-th particle acts force.

We select an element of volume and sum up the forces acting on all the particles of this element of volume. The force acting on all particles in a given volume element is defined as the current density on the magnetic field and on the value of the volume element. And now we rewrite it in a differential form:, hence - this power density, the force acting on the unit volume. Then we get the general formula for strength:.

  Usually the current flows along linear conductors, rarely do we encounter cases where the current is smeared somehow in volume. Although, by the way, the Earth has a magnetic field, but from what is this field? The source of the field is the magnetic moment, which means that the Earth has a magnetic moment. And this means that the recipe for the magnetic moment shows that there must be some kind of current inside the Earth, they must of necessity be closed, because there can be no stationary open field. Where do these currents support them? I am not an expert in terrestrial magnetism. Some time ago, a certain model of these currents was not yet. They could have been induced there once and had not yet faded away there. In fact, the current can be excited in a conductor, and then it quickly ends by absorption of energy, heat, and other things. But, when we deal with such volumes as the Earth, then there is a damping time of these currents, once with some kind of excited mechanism, this damping time can be very long and last for geological epochs. Maybe it is. Well, let's say, a small object like the Moon has a very weak magnetic field, which means that it has already been damped there, say, the magnetic field of Mars is also much weaker than the field of the Earth, because Mars is less than Earth. This is what I? Of course, there are cases when the currents flow in volumes, but the fact that we here on Earth have usually linear conductors, therefore, we are now transforming this formula with reference to a linear conductor.

Suppose there is a linear conductor, the current flows with the force I. Select the element of the conductor, the volume of this element dV. The force acting on the element of the conductor is perpendicular to the plane of the triangle, built on the vectors and, that is, directed perpendicular to the conductor, and the total force is summed. Here, two formulas solve this problem.

Magnetic moment in the external field

The magnetic moment itself creates a field, now we don’t consider its own field, but we are interested in how the magnetic moment behaves when placed in an external magnetic field. A moment of force, equal to, acts on the magnetic moment. The moment of force will be directed perpendicular to the board, and this moment will tend to turn the magnetic moment along the line of force. Why does the compass needle point to the north pole? She, of course, does not care about the geographic poles of the Earth, the compass needle is oriented along the magnetic field line of force, which, by chance, is directed along the meridian approximately. Due to what? And it affects the moment. When the arrow, the magnetic moment that coincides in direction with the arrow itself, does not coincide with the power line, a moment appears that turns it along this line. From where the magnetic moment is taken from the needle of the compass, we will discuss this later.

In addition, an equal force acts on the magnetic moment. If the magnetic moment is directed along, then the force pulls the magnetic moment into the area with greater induction. These formulas are similar to the way the electric field acts on the dipole moment, there too the dipole moment is oriented along the field and is drawn into the area with greater intensity. Now we can consider the question of the magnetic field in matter.

Magnetic field in matter

  Atoms can have magnetic moments. The magnetic moments of atoms are associated with the angular momentum of the electrons. The formula has already been obtained, where is the angular momentum of the particle creating the current. In the atom, we have a positive nucleus and an electron e, rotating in orbit, in fact, at one time we will see that this picture has no relation to reality, so it is impossible to imagine an electron that rotates, but the fact remains that an electron in an atom has an angular momentum, and this angular momentum will respond such a magnetic moment:. Visually, the charge rotating in a circle is equivalent to a circular current, that is, it is an elementary turn with a current. The moment of an electron's momentum in an atom is quantized, that is, it can take only certain values, according to this recipe:, where this value is Planck's constant. The angular momentum of an electron in an atom can take only certain values; we will not discuss now how this happens. Well, and because of this, the magnetic moment of an atom can take on certain values. These details do not concern us now, but at least we will imagine that an atom may have a certain magnetic moment, there are atoms that do not have a magnetic moment. Then the substance placed in the external field is magnetized, and this means that it acquires a certain magnetic moment due to the fact that the magnetic moments of the atoms orient themselves mainly along the field.

Volume element dV   acquires a magnetic moment, for which the vector has the meaning of the density of the magnetic moment and is called the magnetization vector. There is a class of substances called paramagneticsfor which, it is magnetized so that the magnetic moment coincides with the direction of the magnetic field. Are available diamagneticwhich are magnetized, so to speak, “against the wool,” that is, the magnetic moment is anti-parallel to the vector, which means. This is a more subtle term. The fact that the vector is parallel to the vector is clear, the magnetic moment of the atom is oriented along the magnetic field. Diamagnetism is associated with another: if an atom does not possess a magnetic moment, then it acquires a magnetic moment in an external magnetic field, and the magnetic moment is antiparallel. This very subtle effect is due to the fact that the magnetic field affects the planes of the orbits of the electrons, that is, it affects the behavior of angular momentum. The paramagnet is drawn into the magnetic field, and the diamagnetic is pushed out. So that it would not be pointless, copper is a diamagnetic and aluminum is a paramagnet, if you take a magnet, the aluminum cake will be attracted by a magnet, and then the copper will repel.

It is clear that the resultant field, when a substance is introduced into a magnetic field, is the sum of the external field and the field created by the magnetic moment of the substance. Now we turn to the equation, or in differential form. Now this statement:   magnetization of a substance is equivalent to induction in it of a current with a density   . Then we write this equation as.

Check the dimension: M   - is the magnetic moment in a unit of volume, dimension. When you write any formula, it is always useful to check the dimension, especially if this formula is your own brood, that is, you did not copy it, did not remember it, but received it.

Magnetization is characterized by a vector, it is called the magnetization vector, it is the density of the magnetic moment or the magnetic moment per unit time. I said that magnetization is equivalent to the appearance of a current, the so-called molecular current, and this equation is equivalent to this: that is, we can assume that there is no magnetization, but there are such currents. Let us set ourselves by the following equation:, are the real currents associated with specific charge carriers, and these are currents associated with magnetization. An electron in an atom is a circular current, we take the area inside, inside the sample all these currents are destroyed, but the presence of such circular currents is equivalent to one common current that flows around this conductor along the surface, hence this formula. Rewrite this equation in the following form:,. This will also be sent to the left and denote, the vector is called magnetic field strengththen the equation takes the form. (Circulation of the magnetic field strength in a closed loop) = (current strength through the surface of this circuit).

Well, finally, the last. We have the following formula:. For many media, the magnetization depends on the field strength, where - magnetic susceptibility, is the coefficient characterizing the propensity of the substance to magnetization. Then this formula will be rewritten in the form, - magnetic permeability, and we get the following formula:.

If, then these are paramagnetic, are diamagnetic, well, and, finally, there are substances for which it takes large values ​​(of the order of 10 3), these are ferromagnetics (iron, cobalt and nickel). Ferromagnetics are wonderful themes. That they are not only magnetized in a magnetic field, but residual magnetization is characteristic of them, if it has already been magnetized once, then if the external field is removed, then it will remain magnetized unlike diamagnetic and paramagnetic. A permanent magnet is a ferromagnet, which is magnetized by itself without an external field. By the way, there are analogues of this case in electricity: there are dielectrics that are polarized by themselves without any external field. In the presence of matter, our fundamental equation takes the following form:

And here's another example   ferromagnetic, household example of a magnetic field in environments, firstly, a permanent magnet, well, and a more subtle thing - tape. What is the principle of writing to tape? A tape recorder is a thin tape covered with a layer of a ferromagnet, the recording head is a coil with a core over which alternating current flows, an alternating magnetic field is created in the gap, the current tracks a sound signal, vibrations with a certain frequency. Accordingly, there is an alternating magnetic field in the circuit of the magnet, which varies with this current. Ferromagnet is magnetized by alternating current. When this tape is pulled through a device of this type, the alternating magnetic field creates a variable emf. and the electrical signal is played again. These are ferromagnets at the household level.

Quasistationary fields

The prefix "quasi-" is the Russian equivalent of "supposedly", that is, it means that the field is variable, but not very. Now we suppose, finally, but we will leave one thing: in order not to take into account the influence of the electric field on the magnetic field. Maxwell's equations take the following form:

3) and 4) the equations have not changed, it means that the connection of the magnetic field with the currents at each point remains the same, only we now allow currents varying with time. The current may change over time, but the relationship between the magnetic field and the current remains the same. Since the magnetic induction is linearly related to the current, it will change synchronously with the conductor current: the current increases, the magnetic field increases, but the connection between them does not change. But for the electric field, a novelty appears: circulation is associated with a change in the magnetic field.

Electromagnetic induction phenomenon

A connection is found between electric and magnetic fields, if the magnetic field changes with time. An alternating magnetic field is a source of a vortex (closed) electric field. The epithet “vortex” is not some kind of metaphor, but it simply means that the lines of force of the electric field are closed. The phenomenon of electromagnetic induction is described by the equation.

Magnetic flux, “flux” is a term, you should not think what is flowing there, it’s just such a quantity. If the field is uniform and the ground is perpendicular to the lines of force, then for this case; if the site is oriented so that the normal to it is perpendicular to the lines of force, that is, the magnetic field slides along this surface of the site, then the flow will be zero. Clearly, the value of F is the number of lines of force crossing this site. This number actually depends on how thickly we draw them, but nevertheless these words make sense. We have a uniform magnetic field. Here, I'll take pad 1, here is one stream, now I'll take the same pad, but I will be located at point 2. Here (at point 1) it is crossed by five lines of force, and here (at point 2) there are only two. And no matter how I paint them thickly, the picture would not change.

What does the law say? And the law states this: take a closed loop, the surface rests on this loop S, we calculate the magnetic flux through the surface, and the law states if the magnetic flux through the surface supported on the contour changes with time, that is, the circulation of the intensity along the contour is not equal to zero and is equal to. This means that on average there is a component of the electric field along this circuit, all the time directed in one direction.

If I take the wire loop, the magnetic flux through the area will change, then this circuit will appear electricity. This phenomenon is called the phenomenon of electromagnetic induction.

The phenomenon of electromagnetic induction - is the appearance of a current in the circuit, if the magnetic flux changes through this circuit.

Electromotive force

The integral is designated and this quantity is called electromotive force. What is the meaning of the term? At one time, the forces called anything that is falling; now the word “force” is used in one sense: the right side of Newton's Second Law. And just the legacy of these old times, the electromotive force applied to this value.

Quasistationary currents

Here is the quasistationary condition for current:. What does this equation mean? The equation states that the circulation of the magnetic field strength is equal to the total current that flows through the surface of this circuit. And now I’ll do this: take the surface (bubble) that rests on the contour, and now I tighten the neck. When I contour this contour to a point, this left side tends to zero, because nowhere can it reach infinite values, but what is done with the right side? The surface becomes closed when the contour is tightened to a point. From these arguments we get that. This is the condition of quasi-stationary current. Physically, this means that: what kind of charge per unit time flows into a closed surface, such a charge flows. This means in particular the following: if there are three conductors, the consequence of the statement will be that. We cover the point of intersection with a closed surface, since the currents flowing in per unit of time and flowing are equal, which means that.

Ohm's law

For metal conductors with good accuracy is such a law:, where the value is called conductivity, it is some constant that characterizes the ability of the conductor to conduct current. This is a law in differential form, what relation does it have to a law that you know well? This result, by the way, will get it for the cylindrical conductor.

Ohm's law for a circuit with emf

On the other hand, we already know that for a capacitor, from here. q, I - functions of time, purely formally, one function must be expelled. Cover the plate with a closed surface (current density in the conductor on the conductor cross section is the current strength). We make up the system of equations, whence we get the differential equation, which is immediately solved: Our initial conditions are: t = 0, q (0) = q 0, Consequently A = q 0. .

Self-induction phenomenon

This is a special case of electromagnetic induction. A current flows along the contour, an alternating magnetic field arises, Ф =, emf, which is induced in the contour is:,. This phenomenon is called self-induction. , L   - self-induction coefficient (self-inductance), depending on the geometry of the circuit and on the environment. Then we got this law:.

Inductance of the long solenoid

  Consider one turn:, therefore. It is in one turn, and full emf. is the summation over all the turns:, the coefficient before - the coefficient of self-induction.

Here is the question: we have a coil, what will happen if the ends of this coil are inserted into the socket? I was interested in this question from my childhood, in this connection: it was a long time ago and there were various space flight projects, as one of the projects was this: to make a long solenoid (such a magnetic gun) in it a projectile (a metal spacecraft), and such a magnetic field in a long tube, he would have to accelerate, shoot and fly. I had such a book, there was this one of the projects, well, and I decided to look. He took up a cardboard tube, wrapped a wire around it, put an iron thing in there and put it in a socket to see if it would fly. The effect was, of course, impressive when it all burned with a terrible flash. But the problem itself, what will happen if the coil winding stick into the outlet, it takes me since. Here's the question: what will happen if you take the coil wrapped and put it in the socket? The answer is this: if there are a lot of turns there, then the resistance of this winding will be zero, an alternating current will flow such that emf. self-induction at each point in time will balance the voltage at the outlet terminals, the greater the inductance of the coil, the less current will be, and nothing spicy will happen, at a constant current it will burn, for direct current   such a coil will be short circuit. Alternating current   - A coil with an arbitrarily small resistance, if it has a large enough inductance, you can stick in, and nothing terrible will happen.

Magnetic field energy

We have already asked a similar question for the electric field and found that it is impossible to create a free electric field; this requires energy and, consequently, financial costs. With a magnetic field in the same way: you cannot create a magnetic field for nothing. In order to create a magnetic field, it is necessary to do a certain work, we will now calculate it.

With an increase in the current in the circuit, an emf occurs, equal. This emf directed "against the wool" (against the current). To maintain this current, power is required. So, the work that needs to be done in time dt   equals: Moral: in order to increase the current strength dÁ, need to do work dA   such (it is determined by the already available current by the time t). Complete work will be integral:. In order to create a current Á, work is needed, where L   - self-induction coefficient.

And now I ask, where does this work go? Answer: stored in the form of magnetic field energy. Clearly: we have a generator with a pen, we twist this pen. The work that we do, turning this knob, goes into the energy of a magnetic field and spreads across the whole space.

Let the magnetic field localized in a long solenoid, then the work is:, but, and, and we get:. This work is equal to the energy of the magnetic field: the value has the meaning of the energy density. The volume element contains energy, and the volume V - .

The magnetic field has energy, and the density of energy, can it be released? Yes, of course, if the magnetic field disappears, then this energy is released in one form or another.

Creating current in a circuit with inductance

This is the creation of a current in any circuit, because any circuit has inductance. We have such a system: battery, key, R   - resistance of the circuit L   - inductance of the circuit (it is not necessary to have a coil, because, I repeat, any circuit has an inductance, but we draw it). We have a rule for a closed loop:. In this case, if the current in the circuit changes, then we have an emf. batteries, external forces concentrated there, and in addition, due to self-induction, emf develops. We write: (- is the emf of self-induction), we get the following equation:, or, or. Such a differential equation, linear, first degree, inhomogeneous, is solved by:. Define BUT   from the initial conditions:, it means that. We then finally get: When we get - a reasonable solution, and the initial stage - an exponential increase:

Why, it is asked, when you turn on the light, does it flash instantly? The answer is: the inductance is just small. If, for example, you put a good coil in series with a light bulb and use alternating current, then the lamp will not light at all, if you connect it to the battery, then the light bulb will slowly light up, but when you turn it off, there is also an interesting thing to happen: Magnetic field is the release of energy, thunder, lightning, etc.

We have finished the discussion of quasi-stationary processes. Now we move on, and the last topic we have in electricity is non-stationary fields.

Non-stationary fields

Bias current

Non-stationary fields are described by the full set of Maxwell's equations without any exceptions:

What we have so far considered are four equations. But in the fourth a term was removed. We begin the elucidation of the role of this term.

By the way, the whole set is called "Maxwell's equations", why? The first equation is in fact the Coulomb law; the second is the law of electromagnetic induction, which Faraday discovered; the third one expresses the fact that the magnetic induction lines are closed, it is even difficult to specify the authorship here; Now, if we throw out this term, then the fourth equation is the law of Bio-Savart. What did Maxwell do? One thing: he added this addendum to one equation, and the whole set was called the "Maxwell's equation".

And now, here, I can not say whether Maxwell argued, but you can give an example on which this equation would break. Here is an example. Consider a spherically symmetric charge distribution, and let the charge spread in this way: let's say we have a charged ball and the charge spreads out of this ball along radial rays. And now it is asked: what magnetic field creates such a spherically symmetric current? Well, since our source is spherically symmetrical, the magnetic field must also be spherically symmetrical. What does this mean? The picture of the field must be such that if this field is rotated around any axis passing through the center of symmetry, it must pass into itself. Perfectly. But from equation 3. it follows that the magnetic field lines are closed, we have already discussed this, and it is impossible to create a configuration of such closed lines so that it has spherical symmetry. Axial symmetry can be, that is, so that the field transforms into itself when turning around a certain axis, and that it transforms into itself when turning around any axis ... If you strain your imagination, it is clear that you cannot create spherically symmetric magnetic fields from closed lines. From equation 3. it follows that for such a spherically symmetric current, that is, a magnetic field is not created, that is, a magnetic field is not created.

Take such a contour, a contour whose area is perpendicular to the current lines. Let's apply here the equation 4 * to this contour. - the circulation through this circuit is not zero. Why? Because the equation says that the circulation is equal to the current density multiplied by this pad. The current flows through this area, and, once the current flows, the circulation through this circuit is equal to the strength of the current through this area, in any case, not zero. So, it turns out, from the third equation it follows that, and from equation 4 *. follows that. It turned out that two equations compete in relation to this situation. What conclusion, and what, generally speaking, is it true, does this configuration create a magnetic field or does it not create? Symmetry considerations are more powerful considerations, which means that it is true that, that is, the third equation wins. This means that the fourth equation with an asterisk is not true. But, if we add this term, then there are no contradictions between these two equations.

One more consideration, I repeat, I do not know whether it occurred to Maxwell or not, but it could have occurred to it, and probably it did. For an electromagnetic field in a vacuum, equation 2. gives:. Here, when a partial derivative is written, it means that the contour is fixed in space, the contour does not move. Its meaning is such that if it changes with time (not that the circuit has moved somewhere), then an electric field arises. Equation 4 *. gives for empty space, because there is no in emptiness. Symmetry is broken, that is, generally speaking, it would be nice here if the circulation along the equals the flow from the derivative. What physics is behind this equation? An alternating magnetic field creates an electric field, and an alternating electric field creates nothing. Here, symmetry considerations in today's physics are very popular, well, because this is the key to many problems, symmetry breaking is annoying and needs to be explained. In fact, if we take the full equation of 4., then the real equation in vacuum will give the following:. Equation 2. Faraday discovered experimentally, and this is a symmetrical phenomenon of electromagnetic induction - this is Maxwell sucked from the finger. There were no experimental data for this, because, in fact, this effect is very difficult to observe (the constant is very small), and it was almost impossible to create an alternating electric field and detect the occurrence of a magnetic field at that time. It was possible to play on very large derivatives, in short, simply moving an electric charge, a noticeable magnetic field will not be created, say, if you pull this charge with a frequency of a million oscillations per second, you would notice a magnetic field. If you move a charge, according to equation 4., a magnetic field will be created, but so small at moderate frequencies that it is practically impossible to detect it. Maxwell wrote it by analogy, the result was the existence of electromagnetic waves, which no one even thought of before Maxwell. And when, after about twenty years, electromagnetic waves were discovered, then this Maxwell theory and this equation 4 were recognized. Finally, all these constructions turned from a hypothesis into a theory.

The quantity (this quantity, in dimensioning equal to the current density) is called bias current. The name belongs to Maxwell, the name remains, and the argument is gone: nothing shifts there, and the name “bias current” should not cause you to be associated with the fact that something is shifting there, this is a term that remained for historical reasons.

The moral is: an alternating electric field itself creates a magnetic field. And everything closes! An alternating magnetic field is a source of electric, an alternating electric field is a source of magnetic, and equations in vacuum acquire a symmetric form (the only difference is in the sign before the derivative, but this is not such a terrible violation of symmetry).

The introduction of this bias current in the first example saves the matter: in this picture and. In short, the circulation along any circuit is zero. Thus, the fourth equation for this spherically symmetrically spreading current gives that the magnetic field is zero. This Maxwell Amendment put things in order, and the theory became non-contradictory.

The law of conservation of energy for the electromagnetic field

I will write Maxwell's equations in differential form:

Now we do the following: equation 2) I will multiply the scalar by, equation 4) I will multiply the scalar by:

Now, from the second equation we subtract the first:

For uniform dielectric. These were suggestive considerations, in fact, in the general case, as well. Then the equation takes the form: or

There is a Gauss theorem that reduces the integral in volume from divergence to a surface integral. I have an identity, I have a letter S   I'm already busy, so I'm writing σ . Then we choose some space in space. V, σ   - the surface bounding it, and we get such a thing:. There is no current in the vacuum, and we get the equation (9.1).

Let me remind the law of conservation of charge:. What is the meaning? If the charge decreases, then due to the fact that it flows through the surface, limiting the volume.

Now we look at the formula (9.1): the rate of change w   in volume is expressed through a change in the vector through this surface. The structure is the same, the question is what is w   and what is it? What wwe already know: this electromagnetic field energy density, the energy density of the electromagnetic field in a unit volume. Then the integral is the total energy of the electromagnetic field in volume. this is the energy flowing through the unit area per unit of time, and this is the density of the energy flow ( poynting vector), by dimension = W, a =.

This is the work of the electromagnetic field in a unit volume. This work can manifest itself in the form of heat or in the form of work, if there is a motor there, for example.

And now the application of this theorem. Such a chain (see fig.9.2.), the circle indicates the motor. The key is locked, the motor spins, and I wish to apply this theorem. I take a closed surface σ then we get it. Integral is the power of an electric motor or work per unit of time,. The motor does work due to the energy that flows into the volume. This is what I say? The motor performs work due to the fact that the field energy, which is represented by the Poynting vector, flows out of a vacuum through a closed surface with which it can be covered. This means that in order for the electric motor to work. In the neighborhood must be two fields, as.

Energy is transmitted through empty space and flows into this volume. The question then is, why does the electrician fool around and pull the wires from the source to the consumer? The answer is obvious: the wires are needed in order to create such fields and the corresponding configuration. Then the question is different, is it possible to create such fields so that energy is transmitted through emptiness without conductors? It is possible, but this is the next time. So, all end.

Last time we looked at the Poiting vector. Let me remind you, the energy of the electromagnetic field is transmitted through empty space, not through wires. In general, the situation here is this: there is some area, some energy is being poured into this area (say, a shaft with a handle sticks out of this area and then the person turns this shaft) and further this energy flows into another area through empty space, for example, there is a device that processes the energy flowing in here and, at the output, again produces some work (say, there is a generator or an electric motor).

Electromagnetic waves

I have already said that Maxwell perfected the equations (he added a bias current there), and finally a closed theory came out, and the prediction of the existence of electromagnetic waves was the crown of comprehension of this theory. It is necessary to understand that no one saw Maxwell before these waves, no one even suspected that such things could be. But, as soon as these equations were obtained, of them mathematically it followed that electromagnetic waves must exist, and twenty years after this prediction was made, they became observable, and then the theory was a triumph.

Maxwell's equations allows the existence of a thing called an electromagnetic wave. But in nature, it turns out that the fact that it is possible within the framework of the correct theory actually exists.

Now we will have to see, following Maxwell, that there must be these waves, that is, to make such a mathematical discovery, so that, looking at Maxwell’s equations, say: “And, of course, there must be waves”.

Maxwell's equations in the void

What is great about emptiness? In the void there are no charges,. The equations take the form:

Well, the remarkable symmetry immediately catches your eye, symmetry is broken only by the fact that in equation 4) the constant is dimensional and sign. Dimensional constant is not essential, it is connected with the system of units, it is possible to choose such a system of units where this constant is simply a unit. These are differential equations, but the situation is complicated by the fact that the variables intersect. First, we set a modest task - to write an equation that would contain only one unknown quantity, for example.

Hence, our first goal is to exclude from equation 2). How to exclude? And it's very simple: we see that in the fourth equation there is a variable, if we act on this equation as a vector operator, then the right side will jump out ...

The second equation gives:. Adding the fourth equation we get: or

We obtained an equation that states that the second time derivative of is related to the second derivatives of the components with respect to the coordinates, that is, the change in the value at a given point over time is linked to the spatial change in this value.

Wave equation and its solution

Here is a purely mathematical problem:

the equation of the form, where is a function of coordinates and time, and a constant, is wave equation.

We will not solve the partial differential equation, and I will now present one important particular solution, and it will be proved that it really is a solution.

Statement. The view function satisfies the wave equation (partial solution).

A particular solution, in fact, is guessed and checked by typing. Here, we now substitute this solution in the equation and check. What does the equation say? That the second time derivative of this function coincides with the spatial derivatives.

This is why the complex exponent is remarkable: one could write real sines and cosines, but it is much more pleasant to differentiate the exhibitors than sines and cosines.

So Again, a wonderful thing: the operator acts on a function, this function simply multiplies by, then we immediately find the repeated action of the operator:.

Substitute in the original equation:, hence we get.

The moral is this: the function of the form satisfies our equation, but only under this condition:

This is a mathematical fact. It remains for us to figure out now what this function depicts.

If we go into a real domain, that is, we take the restriction of this set of functions to the class of real functions, this will be a solution of this type:. In order not to suffer with three variables, it is possible to simplify this matter: let, then. Note that this is no limitation of generality, the axis x   we can always choose along the vector. We obtained a function from two variables:. And now we will see what this function represents.

We make an instant photo: we fix the moment of time and look at the spatial configuration.

The period of the sine of 2π is clear when x   changing to λ – wavelength   (spatial period), the sine should change by 2π, we have the following ratio:. We interpreted the constant k – wave numberand the vector is the wave vector. This instant photo shows how the function depends on the space.

Now we will follow the temporary change, that is, we sit at the point x   and see what happens with the function over time. We fix, then, then, at a fixed point, again, the sinusoidal function of time. We have, since the period of the sine of 2π, that is, we have interpreted a constant, is called by frequency.

And finally, the last thing remains: run both variables λ   and tWhat then will this feature represent? Easy to understand too.

If, then, and means in turn that. For events for which the coordinate is a linear function of time, the function is always the same. This can be interpreted as follows: if we run along the axis x   with speed, we will always see in front of us the same value of this function.

The function we got is a sine wave traveling right along the axis x.

If we run x   and t   at the same time, it turns out that this sinusoid runs along the axis at a speed, we received such a solution, and then it is clear why this is called a wave.

Here is what I said, that if we run at such a speed, we will see the same value of the function, clearly:

water waves. For a wave in water, this is the deviation of the wave from the horizontal level. When you run along this wave with the speed of its propagation, you will always see in front of you the same height above the surface of the water.

Another example - sound wave.

We have a sinusoidal sound wave. How to create it? The source oscillates with one frequency (we seldom perceive such a hum on one frequency, which, by the way, is very annoying). If there is such a wave of a certain tonality, then when you are standing, the pressure in your ear changes with time and creates a force that puts pressure on the membrane in the ear, vibrations of the membrane are transmitted to the brains, using different transmission devices there, and we will hear the sound . And what will happen if you run along the wave with the speed of its spread? There will be constant pressure on the membrane and everything, there will be no sound. True, the example is hypothetical, because if you run in the air at the speed of sound, then you will have to whistle in your ears so that you will have no time for perceiving this string.

The wave runs with speed, but we have this ratio:. We see that speed is the constant in the equation.

The solution of the wave equation is a sine wave traveling at a speed with.

Now back to the Maxwell equations. We got there that. For the magnetic field is similar. Such a function satisfies this equation. Provided that. So, there must be electromagnetic waves propagating at such a speed. And here the circle is closed. Maxwell obtained the wave equation and determined the wave velocity, and by that time the experimental value of the speed of light was known, and it was found that these velocities are equal.

The computer would have considered it: it would break the curve into elements with a given accuracy and sum it up. How to get into the computer vector field? Table: the space is divided into cells and enter the value of the vector in each cell, the curve is also entered in a table. There are ways in the analysis of how to take such integrals, but we don’t care now, we need to understand the meaning.

) Here I introduced a new mathematical symbol - a partial derivative, but so that there were no misunderstandings:. It is more convenient to write instead, because it directly contains an indication of what needs to be done.

By the way, here, in the exercise order, it would be useful for you to calculate, and make sure that you get the previous formula for field strength. This, here, for a self-test (not in physics, but in mathematical qualification), if you get it - this is a sign that you have a corresponding mathematics, if not, then go to your teacher. analysis, and let him there you either teach or punish.

A field created by a given charge distribution.

) Any charge distribution considered from infinity, well, or from a distance, it always behaves like a point charge.

) Integration is carried out according to when integration is performed, then this variable takes off altogether, we get a number, it sits here as a parameter, that is, the value of the integral depends on, on the position of the point where the potential is sought.

) The obvious thing is that if we move far enough away from this distribution, then what field will it be? Like a point charge. So, at a great distance, you can write the answer immediately: the potential as from a point charge.

) This is still an exact formula, there is a small value and a square of a small value; now, if we threw them out, we would get a point charge field, we’ll throw out a small square and make the formula more accurate.

) Integration is carried out by the hatched variable, by the coordinates of the volume element, relative to this integration.

) There is a whole section of mat. physicists specifically dedicated to solving this equation, and we will not discuss this.

) The word "capacity", in general, is unfortunate, because it leads to household associations, such as the capacity of a bucket or a cup capacity, in fact, there is no such meaning. This I simply warn you, because there are often misunderstandings; there is a feeling that the capacity of the conductor is connected with the charge that can be put on this conductor; You can put any charge on any conductor, there will be just a different potential, the capacity will be a coefficient of proportionality between potential and charge and everything.

) You should be able to find the capacity of spherical and cylindrical capacitors.

We take into account that the other variables are integrated over and for all - constants.

Integral over BUTD= integral over The sun= 0, since, the integral over CD= 0, because there by assumption. And in the segment AB   vectors and parallel.

The direction of the normal is given by the right screw rule (the bypass and the normal should form the right screw).

It can even be done. It is known that there is radioactive decay (when charged α-particles fly out of the nucleus), take a ball of such radioactive substance from which α-particles fly out (these are positively charged helium nuclei), these charged particles represent this radial current. That is, this situation is realizable.

Physical laws are such that when there is a divergence of a vector in them, then every physicist will certainly have a desire to integrate this divergence in volume.

There is such a mathematical identity. From the first equation, therefore.

We use the formula and take into account that.