Consider now using the Gauss Theorem, the field created by a uniformly charged fine spherical shell. Again, let's start with the consideration of the symmetry of the field. Obviously, the field, as well as the distribution of charges has spherical symmetry. This means that the intensity vector module depends only on the distance to the center of the sphere (or at all points from the center of the sphere in one distance, the intensity module is constant), and the direction is radial, from the center of the sphere to the observation point.
We choose as a closed surface, to which we apply the Gauss theorem, the sphere, concentric with a charged shell (Fig. 251).
Equation for potential point charge looks like that. To use the equation, all you need to do is connect some rooms and solve. If we take this equation for the potential and draw it as a schedule, we will find that electric potential Outside the surface of the sphere looks like this.
It begins with some maximum value on the surface, and then quickly decreases as it moves further. But how about inside the sphere? How about this area of \u200b\u200bgraphics? To do this, we need to think about the fact that the electric field is the rate of potential change. From the Gauss law, we know that the electric field inside the conductive sphere is zero, because the charge on the sphere applies to the surface.
Fig. 251.
Let the radius of the sphere r. More shell radius. Then in all points of this sphere, the vector of tension is directed along the normal to the surface, and its module is constant. Therefore, the stream of tension vector through the sphere is equal to the product of the tension module on the area of \u200b\u200bthe sphere F E \u003d E × 4πr 2. By the Gauss Theorem, this flow is equal to the charge of a sphere divided by an electrical constant F E \u003d Q / ε O. Of the equality of these expressions, we obtain the dependence of the field strength from the distance 
The resulting formula corresponds to the formula of the Culon law for a point charge, therefore, beyond the sphere, the field of a uniformly charged sphere coincides with the field of point charge placed in the center of the sphere. Thus, the result, for the proof of which I. Newton spent several years, we received almost automatically. We emphasize that in addition to the proof of formula (1), in addition to the K. Gauss Theorem, it was necessary to consider the symmetry of the fields.
The field inside the charged spherical shell should also have a spherical symmetry. Therefore, the stream of tension vector electric field through the sphere, concentric with charged shell and located inside it (Fig. 252) 
Fig. 252.
Also expressed formula F E \u003d E × 4πr 2. However, within this sphere electrical charges No, therefore, from Theorem K. Gauss it follows that the field strength inside the sphere is zero. We emphasize if the Gauss Theorem was not fair, then an electric field would exist inside a uniformly charged shell.
Thus, a function describing the field strength of a uniformly charged sphere of radius r.has the form (the graph of this function is shown in Figure 253) 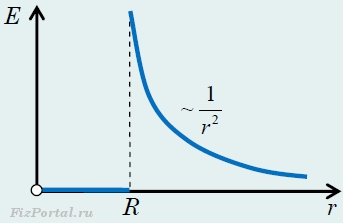
Fig. 253. 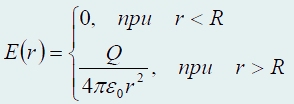
If the electric field is zero across the entire inside of the sphere, this means that the rate of potential change is zero. Or, in other words, the potential within the sphere does not change. So, the schedule must be flat, for example. From the surface, up to the center, the electric potential remains constant.
Two points in space have different electrical potentials due to their different positions inside the field. From the Gauss law, we know that the equation for the electrical field of the conductive charged sphere coincides with the equation for the electric field of the point charge. Electric field It is also a change in the potential. It follows that the equation for the potential of the charged sphere also coincides with the equation of the potential of a point charge. We can build this equation along the radius from the center of the sphere, creating a schedule that looks like in the section above.
The spherical surface of the radius R with a shared charge q is charged evenly with surface density +0. Due to the uniform distribution of charge on the surface, the field created by them has a spherical symmetry. Therefore, the lines of tension are directed radially. We construct a mentally sphere of radius R, which has a common center with a charged sphere. If R\u003e R, the entire charge Q, which creates the field under consideration, falls inside the surface, and, on the Gauss theorem, from where:
The Gauss law also tells us that the electric field inside the conductive sphere is zero. Since the electric field is the rate of capacity change, this means that the potential should not change within the sphere, therefore, for the inner sphere of the sphere, the schedule remains flat, as shown above.
Examine this lesson when you prepare.
- Indicate the definition of the electric potential.
- Denote the equations for the potential obtained from the Gauss law.
- Understand the effect of the electric field to zero inside the conductive sphere.
![]()
At R\u003e R, the field decreases with the distance r along the same law as a point charge. The graph E dependence of R is shown in Fig. 129. If R "< R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (E = 0).
Massive full ball is uniformly charged. Use the Gauss law in combination with the Maxwell equation from the electric field for the electric field. To determine the electrical field outside the full sphere, you can best use the Gauss law in spherical coordinates. It is ideal for this problem, since the full sphere has spherical symmetry, so the Gauss law ensures the fastest solution.
First, imagine or think about the imaginary Gaussian volume that surrounds the charged full sphere and has the same central point. Use the Gausha law to which you use the Maxwell electrostatic equation.: \\\\ \u003d \\\\. However, these parts would be present if the full spheres were not uniformly charged! Use the Gauss law from Notes: \\\\ \u003d \\\\.
14. Vector polarization
Polarization vector - vector physical value equal to the dipole moment of a unit of the volume of the substance arising during its polarization, the quantitative characteristic of dielectric polarization.
It is indicated by the letter P, in the international system of units (C) is measured in CL / m 2.

Now only a single goal. Since this is a spherical task, the Gaussian law leads to a rapid definition of the E-field. To determine the electrical field outside, apply Gaussian the sphere that surrounds the hollow ball. Now you must completely clean the surface! For this spherical task, use spherical coordinates.
Therefore, its amount does not depend on whether you are moving a little to \\\\ or \\\\. If you do not know the formula for the surface of the sphere, you can integrate it on the surface. Now you need to admit that the Gaussian sphere located in the charged field does not include a charge.
15. Relative dielectric constant and its connection with dielectric susceptibility
The dielectric permeability of the medium ε shows how many times the strength of the interaction of two electrical charges in the medium is less than in vacuum. The relative dielectric permeability of air and most other gases under normal conditions is close to one (due to their low density).
Thus, Gauss's law becomes 0 \u003d. Since the surface of the Gaussian sphere is not zero, the electric field should be zero. Calculate the electrical field created by the sphere in all points of space. Application of electrostatic laws Direct integration. . The simplest way to calculate this field is an application of an innocent nature. electrostatic field and Law Gauss.
The fact that the electrostatic field is intimidate, allows you to enter an electric potential. The use of electric potential allows the use of simple symmetries of this problem. Since this is a uniformly charged spherical surface, the system is invariant with respect to rotation around its center.
The relative dielectric permeability of ferroelectrics is tens and hundreds of thousands.
The dielectric susceptibility (polarizability) of the substance is the physical value, the measure of the ability of the substance to polarize under the action of the electric field. Dielectric susceptibility - the linear communication coefficient between the polarization of the dielectric P and the outer electric field E in sufficiently small fields:
Therefore, the electrical potential depends solely on the distance to the center of the sphere. And this means that the electrostatic field is the central field. As soon as it is found that the field is radial and depends exclusively on the distance to the center, we can use the Gauss law to find its value.
According to the law of Gauss. ![]()
Let's go first with the second member. The surface of the integration is within the sphere and does not contain any load, since everything is located outside the surface. 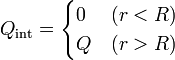
Let's go with the first participant. For spherical surface we must. Therefore, the flow comes down to the integral.
![]()
where - electrical constant; Produced by absolute dielectric susceptibility. In case of Vacuum
Dielectrics are usually positive. Dielectric susceptibility is measured in nothing (dimensionless value).
Polarizability is associated with dielectric constant ε by the ratio: ![]() , or
, or
Therefore, you can leave the integral. It is necessary to insist again and again on the fact that in order for the field to be removed from the stream, this integral must first be transformed into one of the scalar value and this value is constant on the integration surfaces. If not, you cannot remove the field, and the flow is not equal.
Gauss's law is always truthful, but not always useful. Equating now the expression of the flow to the accompanying load divided by the fall. 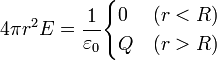
And expression for the field in vector form. Pronounced by words, the electric field created by a uniformly charged sphere is zero inside the sphere and an equal to the electric field of a point charge outside. This punctual charge will cost a complete charge of the sphere and will be located in the center of it.
16. Electric displacement vector
Electrical displacement - vector value equal to the sum of the voltage vector of the electric field and the polarization vector.
In C: D \u003d E + 4πP
17. Theorem Gauss for dielectrics
18. Hytresis loop for ferroelectrics
Now we will solve the same task by direct integration, i.e. Based on the integral expression for the field created by the distribution surface charge. ![]()
Load density, if it is evenly distributed, will be. ![]()
Being a unitary radial vector, we must go to the Cartesian base during integration.
Vector relative position and its module. Since, by determining the angle θ. When replacing in the integral expression for the field, we must pass the integrand to the Cartesian base. From the point of view of view, the charged sphere can be considered as consisting of a rings whose axis passes through this point.
Hysteresis Segroelectric - an ambiguous loop-like dependence of the polarization of ferroelectrics from external. Electric. Fields E with its cyclick. Change. For perfect hinge monocrystals. It has a form close to rectangular, and even to. in real crystals and ferroelectrics. The ceramics of the loop has a different form, is very different from, the process of interpretability is delayed to a large interval of E. values
Each of the rings, as seen from another task, creates a field on its axis, which goes towards this axis. The integral in gives us a multiplier 2π, since the integrand has an azimuth of symmetry. We must, since two radio stations are positive.
That is why we allocate two regions as a result. To write an expression of the electric field there is one last step. But what happens if we have two different points in which we want to find a field and whose values \u200b\u200bdo we want to compare? The solution is to restore the geometric interpretation. In this problem, there is a unitarine, which indicates the direction and direction coming from the center of the sphere to the observation point. But it is only general definition. Thus, the expression of the field for any point of space.
19. Electricity of the ball

20. Electricity condenser

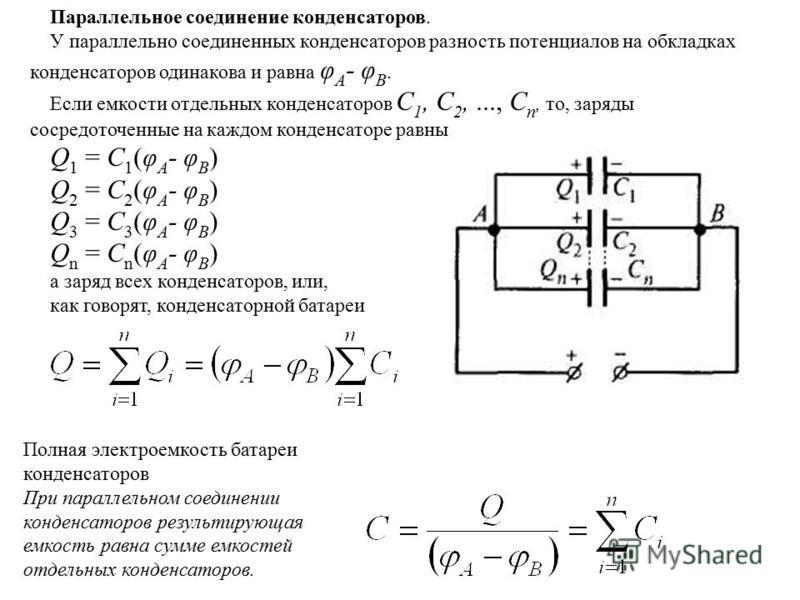
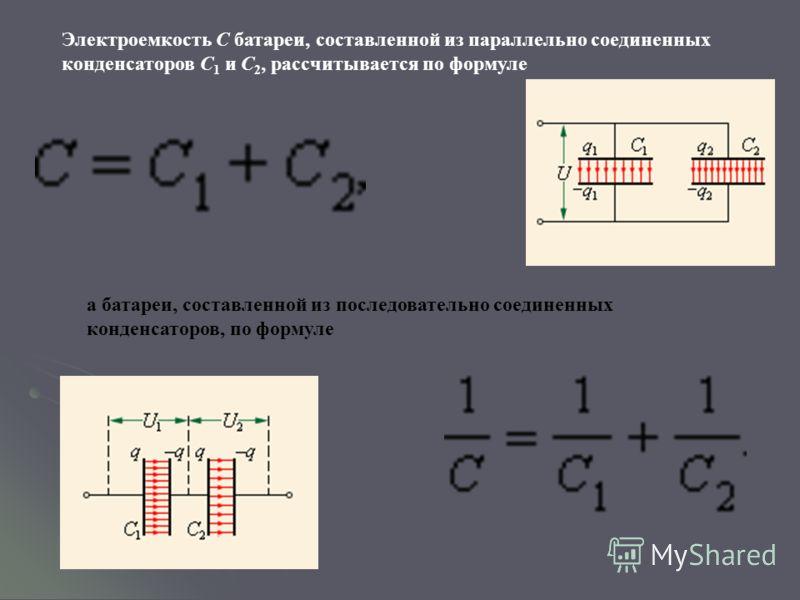
21. Battery power consumption parallel to the connected capacitors
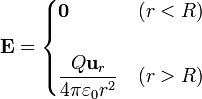
It is strange that the field inside the charged sphere is zero. Obviously, in the center of the sphere should be in symmetry. The result, however, is stronger. The field is zero at all points of the sphere. Seems to be anti-attament that if negative charge Approaches the surface from the inside, do not have a traction force due to charges close to it. Of course, this attraction exists, but compensated by attraction due to the other charges of the spherical surface, which stretch in the opposite direction.
22. Electricity of the battery sequentially connected capacitors
23. Energy of the electrostatic field, bulk energy density


These leisure loads are more distant, but they make up the majority, therefore, finally, both effects are compensated, and the force is zero. This effect is applicable to the gravitational field, since Newton's law is similar to the Culon law. This means that on the hollow planet, his underground residents will not walk along the inside of the planet, but will swim by weightless in the interior.
Square spherical surface. is mathematical representation The fact that the resulting stream is proportional to the number of rows in the field. The number of rows in the field is proportional to the load inside the surface. The number of lines falling on the surface is equal to the number of lines overlooking the surface. The resulting electrical stream through a closed surface, which does not include any charge is zero.
24. The power of the current
Current power (I) - scalar valueequal to the ratio of charge (q), which passed through the cross-section of the conductor, by the interval (T) during which the current was covered.
I \u003d Q / T, where the current is current, Q - charge, T is time.
Unit of current measurement in the SI system: [i] \u003d 1A (amp)
25. Toki density

Electrical field of positive point charge radially outward by symmetry and therefore is normal to the surface at each point. Consequently, it is parallel in all points on the surface, and then according to the law of Gauss. Consequently, where we use the fact that the surface area of \u200b\u200bthe sphere is equal.
Now we get an electric field: - the electric field of a point charge, which we develop from the Coulomb law. Thus, the resulting flow through the Gauss surface is a flow through a flat face outside the conductor, where the field is perpendicular to the surface.
26. EMS.
EMF is the energy characteristics of the source. This is a physical value equal to the attitude of work committed by third-party forces when moving an electric charge on a closed chain, to this charge:
It is measured in volts (B).
27. Ohm's law in differential form
record OMA's law in differential form, where - electrical conductivity [OM -1 M -1]
28. Generalized Ohm Law
Ohm Law: Current Power in Chain direct current Directly proportional to the emf of the current source and inversely proportional to the impedance of the electrical circuit.
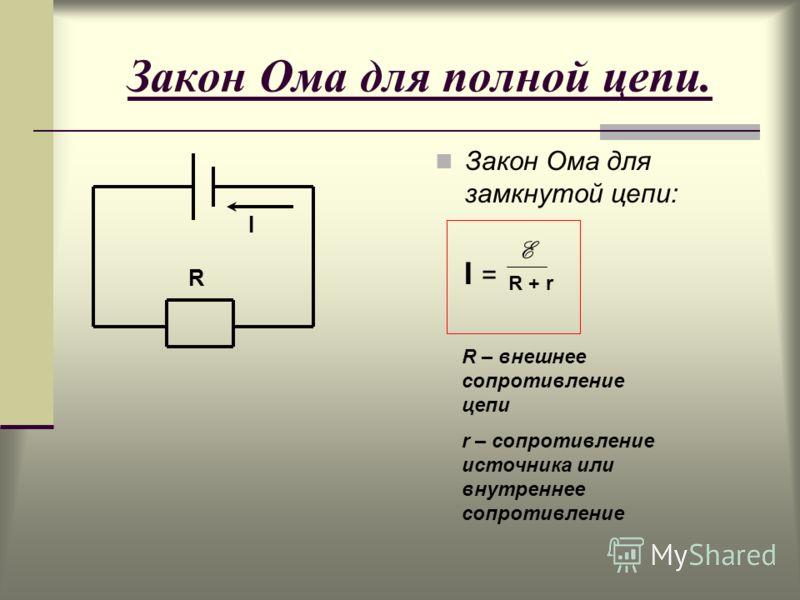
29. The work of the electrostatic field to move charging


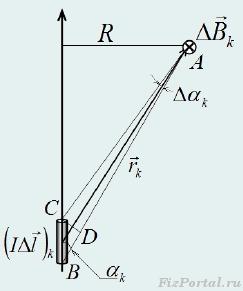
30. Law of Bio-Savara Laplas
The wording of the Law of Bio Savara Laplas has the form: when the direct current is passed on the closed contour, which is in vacuo, for a point, distinguished at a distance R 0, from contour magnetic induction will be viewed.
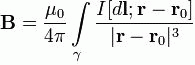
In the event that the progressive movement of the screw is directed towards the current movement, the direction of rotation of the screw head indicates the DB direction.
![]()
31. Induction magnetic field straight wire with current
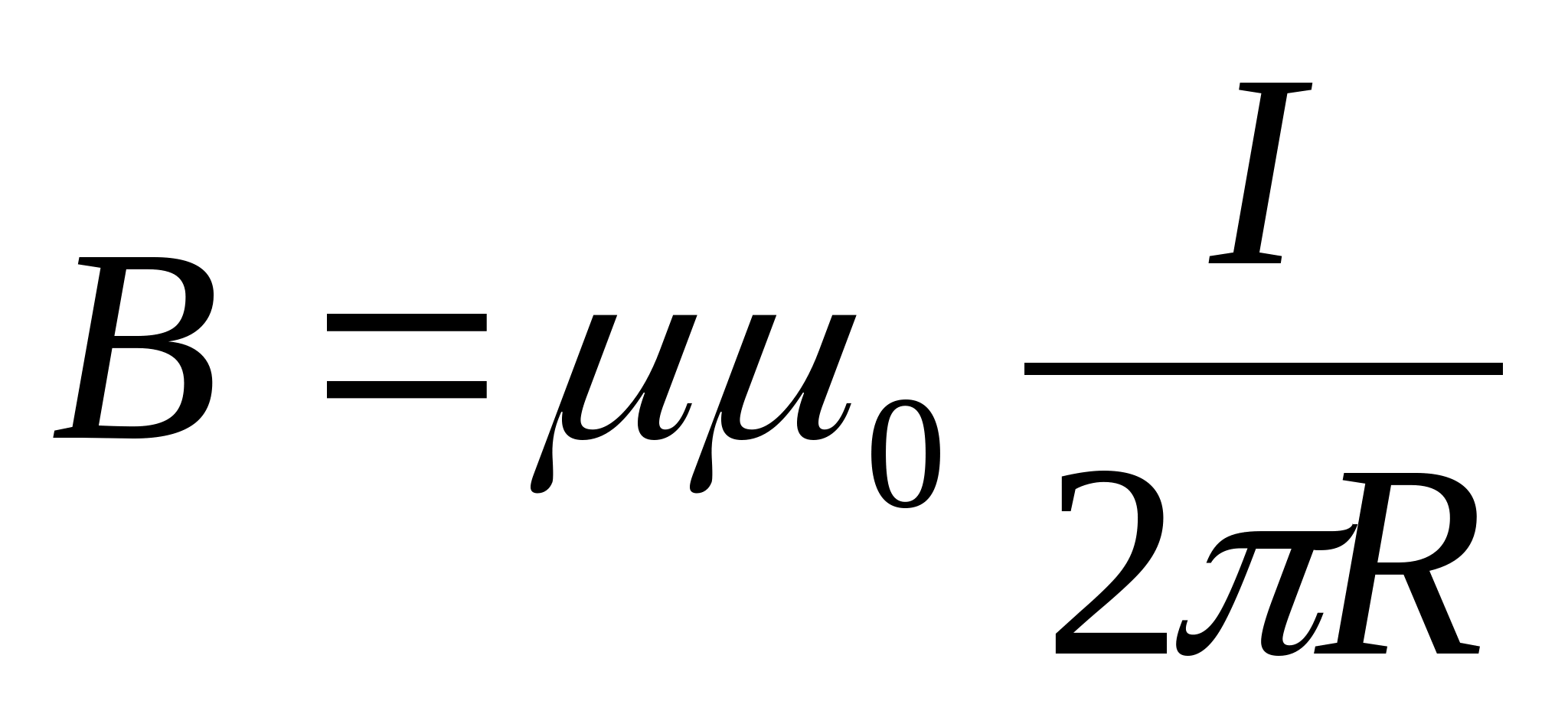
32. The power of amperes The conductor with a current, which is in a magnetic field, acts the force equal toF \u003d i · L · b · sina, where I is the current power in the conductor; B - the module of the magnetic field induction vector; L - the length of the conductor located in the magnetic field; A - The angle between the magnetic field vector and the current in the explorer. Seed, acting on the conductor with a current in a magnetic field, is called the ampere force. The amps of the ampere is: f \u003d i · L · b; it corresponds to a \u003d 90ᵒ
The direction of the ampere power is determined by the rule of the left hand: if the left hand is positioned so that the perpendicular component of the magnetic induction vector is in the palm, and the four elongated fingers were directed towards the current, then the thumb stranded 90 degrees will show the direction of force acting on the conductor segment With current, that is, ampere power.




