مشتق تابع خیلی دور نمی افتد و در مورد قوانین L'Hôpital دقیقاً در همان جهت تابع اصلی قرار می گیرد. این شرایط به افشای عدم قطعیت های شکل 0/0 یا ∞ / ∞ و برخی عدم قطعیت های دیگر که هنگام محاسبه به وجود می آیند کمک می کند. حدنسبت دو تابع بی نهایت کوچک یا بی نهایت بزرگ. محاسبه با کمک این قانون بسیار ساده شده است (در واقع دو قانون و یادداشت برای آنها):

همانطور که فرمول بالا نشان می دهد، هنگام محاسبه حد نسبت دو تابع بینهایت کوچک یا بی نهایت بزرگ، حد نسبت دو تابع را می توان با حد نسبت آنها جایگزین کرد. مشتقاتو به این ترتیب نتیجه مشخصی بدست می آید.

بیایید به فرمول بندی دقیق تر قوانین L'Hôpital برویم.

قانون L'Hôpital برای مورد حد دو کمیت بی نهایت کوچک... اجازه دهید توابع f(ایکس) و g(ایکس آ... و در همان نقطه آ آمشتق از یک تابع g(ایکس) برابر با صفر نیست ( g"(ایکس آبرابر یکدیگر و برابر با صفر هستند:

قانون L'Hôpital برای مورد حد از دو مقدار بی نهایت بزرگ... اجازه دهید توابع f(ایکس) و g(ایکس) مشتقاتی (یعنی متمایزپذیر) در برخی از همسایگی های نقطه دارند آ... و در همان نقطه آممکن است مشتقاتی داشته باشند یا نداشته باشند. علاوه بر این، در مجاورت نقطه آمشتق از یک تابع g(ایکس) برابر با صفر نیست ( g"(ایکس) ≠ 0) و حدود این توابع به عنوان x تمایل به مقدار تابع در نقطه آمساوی با یکدیگر و مساوی با بی نهایت هستند:

سپس حد نسبت این توابع برابر است با حد نسبت مشتقات آنها:

به عبارت دیگر، برای عدم قطعیت های شکل 0/0 یا ∞ / ∞، حد نسبت دو تابع برابر است با حد نسبت مشتقات آنها، در صورت وجود دومی (متناهی، یعنی برابر با یک عدد معین یا نامتناهی یعنی برابر بی نهایت).

ملاحظات.

1. قوانین L'Hôpital همچنین زمانی که توابع قابل اجرا هستند f(ایکس) و g(ایکس) برای تعریف نشده اند ایکس = آ.

2. اگر هنگام محاسبه حد نسبت مشتقات توابع f(ایکس) و g(ایکس) دوباره به عدم قطعیت شکل 0/0 یا ∞ / ∞ می رسیم، سپس قوانین L'Hôpital باید چندین بار (حداقل دو بار) اعمال شوند.

3. قوانین L'Hôpital همچنین زمانی قابل اجرا هستند که آرگومان توابع (x) به یک عدد محدود تمایل نداشته باشد. آو تا بی نهایت ( ایکس → ∞).

عدم قطعیت انواع دیگر را نیز می توان به عدم قطعیت های 0/0 و ∞ / ∞ کاهش داد.

افشای عدم قطعیت ها از انواع «صفر تقسیم بر صفر» و «بی نهایت تقسیم بر بی نهایت»

مثال 1.

ایکس= 2 منجر به عدم قطعیت شکل 0/0 می شود. بنابراین، مشتق هر تابع و به دست می آوریم

مشتق چند جمله ای در صورت حساب محاسبه شد و در مخرج - مشتق تابع لگاریتمی پیچیده... قبل از آخرین علامت مساوی، معمول است حد، به جای x دو را جایگزین کنید.

مثال 2.حد نسبت دو تابع را با استفاده از قانون L'Hôpital محاسبه کنید:

راه حل. جایگزینی یک مقدار در یک تابع معین ایکس

مثال 3.حد نسبت دو تابع را با استفاده از قانون L'Hôpital محاسبه کنید:

راه حل. جایگزینی یک مقدار در یک تابع معین ایکس= 0 منجر به عدم قطعیت شکل 0/0 می شود. بنابراین مشتقات توابع را در صورت و مخرج محاسبه می کنیم و به دست می آوریم:

مثال 4.محاسبه

راه حل. جایگزینی مقدار x برابر به اضافه بی نهایت در تابع داده شده منجر به عدم قطعیت شکل ∞ / ∞ می شود. بنابراین، قانون L'Hôpital را اعمال می کنیم:

اظهار نظر. اجازه دهید به مثال هایی بپردازیم که در آنها قانون L'Hôpital باید دو بار اعمال شود، یعنی به حد نسبت مشتقات دوم برسیم، زیرا حد نسبت مشتقات اول عدم قطعیت شکل 0 است. /0 یا ∞ / ∞.

افشای عدم قطعیت های شکل "صفر ضربدر بی نهایت"

مثال 12.محاسبه

راه حل. ما گرفتیم

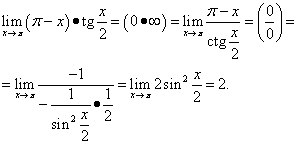
این مثال از هویت مثلثاتی استفاده می کند.

افشای عدم قطعیت ها از انواع «صفر به توان صفر»، «بی نهایت به توان صفر» و «یک به توان بی نهایت»

عدم قطعیت های فرم، یا معمولاً با استفاده از لگاریتم یک تابع از فرم به شکل 0/0 یا ∞ / ∞ کاهش می یابد.

برای محاسبه حد یک عبارت، باید از هویت لگاریتمی استفاده کرد که یک مورد خاص از ویژگی لگاریتم است. .

با استفاده از هویت لگاریتمی و خاصیت پیوستگی تابع (برای فراتر رفتن از علامت حد)، حد باید به صورت زیر محاسبه شود:

به طور جداگانه، شما باید حد بیان را در توان پیدا کنید و بسازید هبه درجه ای که پیدا شد

مثال 13.

راه حل. ما گرفتیم

مثال 14.با استفاده از قانون L'Hôpital محاسبه کنید

راه حل. ما گرفتیم

حد بیان را در توان محاسبه می کنیم

مثال 15.با استفاده از قانون L'Hôpital محاسبه کنید

عدم قطعیت‌های نوع و نوع رایج‌ترین عدم قطعیت‌هایی هستند که باید هنگام حل محدودیت‌ها افشا شوند.

اکثر وظایف تا حدی که برای دانش‌آموزان پیش می‌آیند، فقط دارای چنین عدم قطعیت‌هایی هستند. برای آشکار کردن آنها، یا به طور دقیق تر، برای جلوگیری از ابهامات، چندین روش مصنوعی برای تبدیل فرم یک عبارت در زیر علامت حد وجود دارد. این تکنیک ها به شرح زیر است: تقسیم ترم به ترم صورت و مخرج بر بالاترین توان متغیر، ضرب در بیان مزدوج و فاکتورسازی برای کاهش بعدی با استفاده از راه حل های معادلات درجه دوم و فرمول های ضرب اختصاری.

عدم قطعیت گونه

مثال 1.

nبرابر 2 است. بنابراین، صورت و مخرج را بر جمله تقسیم می کنیم:

در سمت راست عبارت نظر دهید. پیکان‌ها و اعداد نشان می‌دهند که کسرها پس از تعویض به‌جای تمایل به چه چیزی تمایل دارند nمقادیر بی نهایت در اینجا، مانند مثال 2، درجه nبیشتر در مخرج تا در صورت، در نتیجه کل کسر به یک مقدار بی نهایت کوچک یا "عدد فوق کوچک" تمایل دارد.

پاسخ را می گیریم: حد این تابع با متغیری که به بی نهایت تمایل دارد برابر است با.

مثال 2. .

راه حل. در اینجا بالاترین توان متغیر است ایکسبرابر 1 است. بنابراین، صورت و مخرج را بر جمله تقسیم می کنیم ایکس:

تفسیر سیر حل. در صورت حساب، "x" را زیر ریشه درجه سوم می بریم و به طوری که درجه اولیه آن (1) بدون تغییر باقی می ماند، آن را همان درجه ریشه، یعنی 3، نسبت می دهیم. دیگر پیکانی وجود ندارد. و اعداد اضافی در این ورودی، پس ذهنی امتحان کنید، اما با قیاس با مثال قبلی، مشخص کنید که عبارات صورت و مخرج پس از جایگزینی بی نهایت به جای "x" به دنبال چه چیزی هستند.

ما به جواب رسیدیم: حد این تابع با متغیری که به بی نهایت تمایل دارد برابر با صفر است.

عدم قطعیت گونه

مثال 3.عدم قطعیت را کشف کنید و حدی پیدا کنید.

راه حل. عدد تفاوت بین مکعب ها است. بیایید آن را با استفاده از فرمول ضرب اختصاری از درس ریاضی مدرسه فاکتور بگیریم:

مخرج یک مثلث درجه دوم است که ما آن را با حل یک معادله درجه دوم فاکتور می کنیم (یک بار دیگر به حل معادلات درجه دوم اشاره می کنیم):

بیایید عبارت به دست آمده در نتیجه تبدیل ها را بنویسیم و حد تابع را پیدا کنیم:

مثال 4.عدم قطعیت را کشف کنید و حد را پیدا کنید

راه حل. قضیه حد نصاب در اینجا قابل اجرا نیست، زیرا

بنابراین، کسر را یکسان تبدیل می کنیم: صورت و مخرج را در مزدوج دوجمله ای در مخرج ضرب می کنیم و آن را با خرج می کنیم. ایکس+1. با توجه به نتیجه قضیه 1، یک عبارت به دست می آوریم که با حل آن، حد مورد نظر را پیدا می کنیم:

مثال 5.عدم قطعیت را کشف کنید و حد را پیدا کنید

راه حل. جایگزینی مستقیم ارزش ایکس= 0 به تابع داده شده منجر به عدم قطعیت به شکل 0/0 می شود. برای آشکار کردن آن، تبدیل‌های یکسانی را انجام می‌دهیم و در نتیجه حد مورد نظر را به دست می‌آوریم:

مثال 6.محاسبه

راه حل:ما از قضایای حدود استفاده می کنیم

پاسخ: 11

مثال 7.محاسبه

راه حل:در این مثال، حدود صورت و مخرج 0 است:

; ... ما به دست آوردیم، بنابراین، قضیه حد نصاب قابل اعمال نیست.

بیایید صورت و مخرج را فاکتور بگیریم تا کسری را با ضریب مشترکی که به صفر گرایش دارد خنثی کنیم و در نتیجه اعمال قضیه 3 را ممکن کنیم.

سه جمله ای مربع را با فرمول گسترش می دهیم که در آن x 1 و x 2 ریشه های سه جمله ای هستند. پس از فاکتورسازی و تفرج، کسر را با (x-2) لغو کنید، سپس قضیه 3 را اعمال کنید.

پاسخ:

مثال 8.محاسبه

راه حل:در، صورت و مخرج به بی نهایت تمایل دارند؛ بنابراین، با اعمال مستقیم قضیه 3، عبارتی را به دست می آوریم که نشان دهنده عدم قطعیت است. برای رهایی از این نوع ابهام، صورت و مخرج را بر بالاترین درجه استدلال تقسیم کنید. در این مثال، باید تقسیم بر ایکس:

پاسخ:

مثال 9.محاسبه

راه حل: x 3:

پاسخ: 2

مثال 10.محاسبه

راه حل:هنگامی که صورت و مخرج به بی نهایت تمایل دارند. صورت و مخرج را بر بالاترین درجه استدلال تقسیم کنید، یعنی. x 5:

صورت کسر به 1 و مخرج 0 میل می کند، بنابراین کسر به بی نهایت میل می کند.

پاسخ:

مثال 11.محاسبه

راه حل:هنگامی که صورت و مخرج به بی نهایت تمایل دارند. صورت و مخرج را بر بالاترین درجه استدلال تقسیم کنید، یعنی. x 7:

پاسخ: 0

مشتق.

مشتق تابع y = f (x) با توجه به آرگومان xحد نسبت افزایش آن y به افزایش x آرگومان x زمانی است که افزایش آرگومان به صفر میل می کند:. اگر این حد محدود باشد، تابع y = f (x)در نقطه x متمایز نامیده می شود. اگر این محدودیت وجود داشته باشد، می گویند که تابع y = f (x)مشتق نامتناهی در نقطه x دارد.

مشتقات توابع ابتدایی پایه:

1. (const) = 0 9.

3. 11.

4. 12.

5. 13.

6. 14.

قوانین تمایز:

آ)

مثال 1.مشتق تابع را بیابید

راه حل:اگر مشتق جمله دوم بر اساس قاعده تمایز کسری یافت شود، جمله اول یک تابع پیچیده است که مشتق آن با فرمول پیدا می شود:

، جایی که ، سپس

هنگام حل فرمول ها استفاده شد: 1،2،10، a، c، d.

پاسخ:

مثال 21.مشتق تابع را بیابید

راه حل:هر دو عبارت توابع پیچیده ای هستند، جایی که برای اولی، و برای دومی، و سپس

پاسخ:

کاربردهای مشتق.

1. سرعت و شتاب

اجازه دهید تابع s (t) توصیف کند موقعیتشی در یک سیستم مختصات خاص در زمان t. سپس اولین مشتق تابع s (t) آنی است سرعتهدف - شی:
v = s ′ = f′ (t)
دومین مشتق تابع s (t) آنی است شتابهدف - شی:
w = v " = s " = f " (t)

2. معادله مماس
y − y0 = f ′ (x0) (x − x0)،
که در آن (x0, y0) مختصات نقطه مماس هستند، f ' (x0) مقدار مشتق تابع f (x) در نقطه مماس است.

3. معادله نرمال
y - y0 = -1f ′ (x0) (x - x0)،

که در آن (x0, y0) مختصات نقطه ای است که در آن حالت نرمال رسم می شود، f ′ (x0) مقدار مشتق تابع f (x) در این نقطه است.

4. افزایش و کاهش توابع
اگر f ′ (x0)> 0 باشد، تابع در نقطه x0 افزایش می یابد. در شکل زیر تابع به صورت x افزایش می یابد x2.
اگر f ′ (x0)<0, то функция убывает в точке x0 (интервал x1اگر f '(x0) = 0 یا مشتق وجود نداشته باشد، این معیار به ما اجازه نمی دهد ماهیت یکنواختی تابع را در نقطه x0 تعیین کنیم.

5. انتهایی محلی یک تابع
تابع f (x) دارد حداکثر محلیدر نقطه x1 اگر همسایگی نقطه x1 وجود داشته باشد به طوری که نابرابری f (x1) ≥f (x) برای همه x از این همسایگی برقرار باشد.
به طور مشابه، تابع f (x) نیز دارد حداقل محلیدر نقطه x2 اگر همسایگی نقطه x2 وجود داشته باشد به طوری که برای تمام x از این همسایگی نابرابری f (x2) ≤f (x) برقرار باشد.

6. نقاط بحرانی
نقطه x0 است نقطه بحرانیتابع f (x) اگر مشتق f ′ (x0) در آن برابر با صفر باشد یا وجود نداشته باشد.

7. اولین شاخص کافی برای وجود یک افراط
اگر تابع f (x) برای همه x در یک بازه (a, x1) افزایش یابد (f ' (x)> 0) و کاهش یابد (f' (x)<0) для всех x в интервале и возрастает (f′(x)>0) برای همه x از بازه ^ \ infty $ و $ ^ \ infty $.

همچنین، چنین عدم قطعیت هایی را می توان با استفاده از لگاریتم تابع نمایی آشکار کرد، اما این یک روش حل متفاوت است که در مقاله دیگری به آن پرداخته خواهد شد.

فرمول و پیامدها

فرمولمحدودیت قابل توجه دوم به صورت زیر نوشته شده است: $$ \ lim_ (x \ تا \ infty) \ big (1+ \ frac (1) (x) \ big) ^ x = e, \ text (where) e \ تقریباً 2.718 $$

فرمول دلالت دارد عواقب، که استفاده از آنها برای حل مثال هایی با محدودیت بسیار راحت است: $$ \ lim_ (x \ تا \ infty) \ big (1 + \ frac (k) (x) \ big) ^ x = e ^ k, \ text ( کجا) k \ در \ mathbb (R) $$ $$ \ lim_ (x \ تا \ infty) \ بزرگ (1 + \ فرک (1) (f (x)) \ بزرگ) ^ (f (x)) = e $ $ $$ \ lim_ (x \ تا 0) \ بزرگ (1 + x \ بزرگ) ^ \ فراک (1) (x) = e $$

شایان ذکر است که محدودیت قابل توجه دوم را نه همیشه می توان برای تابع نمایی اعمال کرد، بلکه فقط در مواردی که پایه به وحدت تمایل دارد. برای این کار ابتدا حد پایه در ذهن محاسبه می شود و سپس نتیجه گیری می شود. همه اینها در محلول های نمونه پوشش داده خواهد شد.

نمونه هایی از راه حل ها

بیایید نمونه هایی از راه حل ها را با استفاده از فرمول مستقیم و پیامدهای آن در نظر بگیریم. ما همچنین مواردی را که در آن فرمول مورد نیاز نیست، تجزیه و تحلیل خواهیم کرد. فقط کافی است پاسخ آماده را یادداشت کنید.

مثال 1
حد $ \ lim_ (x \ تا \ infty) \ big (\ frac (x + 4) (x + 3) \ big) ^ (x + 3) $ را پیدا کنید
راه حل
بیایید بی نهایت را به حد جایگزین کنیم و به عدم قطعیت نگاه کنیم: $$ \ lim_ (x \ تا \ infty) \ big (\ frac (x + 4) (x + 3) \ big) ^ (x + 3) = \ بزرگ (\ frac (\ infty) (\ infty) \ بزرگ) ^ \ infty $$ حد پایه را پیدا کنید: $$ \ lim_ (x \ تا \ infty) \ frac (x + 4) (x + 3) = \ lim_ (x \ تا \ infty) \ frac (x (1+ \ frac ( 4) (x))) (x (1+ \ فرک (3) (x))) = 1 $$ ما پایه ای برابر با یک گرفتیم، به این معنی که محدودیت قابل توجه دوم را می توان از قبل اعمال کرد. برای انجام این کار، پایه تابع را با تفریق و اضافه کردن یک به فرمول برازش می دهیم: $$ \ lim_ (x \ تا \ infty) \ بزرگ (1 + \ فرک (x + 4) (x + 3) - 1 \ بزرگ) ^ (x + 3) = \ lim_ (x \ تا \ infty) \ بزرگ (1 + \ فرک (1) (x + 3) \ بزرگ) ^ (x + 3) = $$ ما به پیامد دوم نگاه می کنیم و پاسخ را می نویسیم: $$ \ lim_ (x \ تا \ infty) \ بزرگ (1 + \ فرک (1) (x + 3) \ بزرگ) ^ (x + 3) = e $$ اگر نمی توانید مشکل خود را حل کنید، آن را برای ما ارسال کنید. ما یک راه حل دقیق ارائه خواهیم داد. شما می توانید با روند محاسبه آشنا شوید و اطلاعات کسب کنید. این به شما کمک می کند تا به موقع از معلم خود اعتبار بگیرید!
پاسخ
$$ \ lim_ (x \ تا \ infty) \ بزرگ (1 + \ فرک (1) (x + 3) \ بزرگ) ^ (x + 3) = e $$

مثال 4
حل حد $ \ lim_ (x \ تا \ infty) \ بزرگ (\ frac (3x ^ 2 + 4) (3x ^ 2-2) \ بزرگ) ^ (3x) $
راه حل
حد پایه را پیدا می کنیم و می بینیم که $ \ lim_ (x \ تا \ infty) \ frac (3x ^ 2 + 4) (3x ^ 2-2) = 1 $، بنابراین می توان دومین محدودیت فوق العاده را اعمال کرد. به طور استاندارد، طبق برنامه، یک عدد را از پایه درجه جمع و کم می کنیم: $$ \ lim_ (x \ تا \ infty) \ بزرگ (1+ \ frac (3x ^ 2 + 4) (3x ^ 2-2) -1 \ بزرگ) ^ (3x) = \ lim_ (x \ تا \ infty ) \ بزرگ (1+ \ فرک (6) (3x ^ 2-2) \ بزرگ) ^ (3x) = $$ کسر را با فرمول تبصره 2 مطابقت می دهیم. حد: $$ = \ lim_ (x \ تا \ infty) \ بزرگ (1+ \ frac (1) (\ frac (3x ^ 2-2) (6)) \ بزرگ) ^ (3x) = $$ حالا بیایید درجه را تنظیم کنیم. توان باید کسری برابر با مخرج پایه $ \ frac (3x ^ 2-2) (6) $ باشد. برای این کار، درجه را ضرب و تقسیم بر آن کنید و به حل ادامه دهید: $$ = \ lim_ (x \ تا \ infty) \ big (1+ \ frac (1) (\ frac (3x ^ 2-2) (6)) \ big) ^ (\ frac (3x ^ 2-2) (6) \ cdot \ frac (6) (3x ^ 2-2) \ cdot 3x) = \ lim_ (x \ تا \ infty) e ^ (\ frac (18x) (3x ^ 2-2)) = $$ حدی که در درجه $ e $ قرار دارد عبارت است از: $ \ lim_ (x \ تا \ infty) \ frac (18x) (3x ^ 2-2) = 0 $. بنابراین، در ادامه راه حل، داریم:
پاسخ
$$ \ lim_ (x \ تا \ infty) \ بزرگ (\ frac (3x ^ 2 + 4) (3x ^ 2-2) \ بزرگ) ^ (3x) = 1 $$

اجازه دهید مواردی را بررسی کنیم که مشکل مشابه حد قابل توجه دوم است، اما بدون آن قابل حل است.

در مقاله: «محدودیت قابل توجه دوم: نمونه هایی از راه حل ها» فرمول، پیامدهای آن و با توجه به انواع مکرر مشکلات در این موضوع مورد تجزیه و تحلیل قرار گرفت.

نگاه 20

20.1 افشای عدم قطعیت

مثال 1

حد را حل کنید ابتدا بیایید سعی کنیم -1 را در کسر جایگزین کنیم: در این صورت به اصطلاح عدم قطعیت به دست می آید.

قانون کلی:اگر چند جمله‌ای در صورت و مخرج وجود داشته باشد و شکل نامشخص باشد، برای افشای آن شما باید صورت و مخرج را در نظر بگیرید.

برای انجام این کار، اغلب باید یک معادله درجه دوم را حل کنید و / یا از فرمول های ضرب اختصاری استفاده کنید.

شمارنده را فاکتور بگیرید.

مثال 2

محاسبه حد

بیایید صورت و مخرج را فاکتور کنیم.

مخرج صورت: ,

روش ضرب صورت و مخرج در عبارت مزدوج

ما همچنان عدم قطعیت فرم را در نظر می گیریم

نوع بعدی محدودیت ها مشابه نوع قبلی است. تنها چیزی که علاوه بر چند جمله ای ها، ریشه ها را اضافه می کنیم.

مثال 3

حد را پیدا کنید

صورت و مخرج را در عبارت مزدوج ضرب کنید.

20.2 افشای عدم قطعیت

اکنون گروهی از حدود را در نظر می گیریم که، و تابع یک کسری است که در صورت و مخرج آن چند جمله ای وجود دارد.

مثال 4

محاسبه حد

طبق قاعده ما، سعی می کنیم بی نهایت را جایگزین تابع کنیم. چه چیزی در اوج بدست می آوریم؟ بی نهایت. و در زیر چه اتفاقی می افتد؟ همچنین بی نهایت. بنابراین ما به اصطلاح عدم قطعیت گونه را داریم. کسی فکر می کند که و پاسخ آماده است، اما در حالت کلی اصلاً اینطور نیست و شما باید از تکنیک های راه حلی استفاده کنید که اکنون آنها را بررسی می کنیم.

چگونه محدودیت های یک نوع معین را حل کنیم؟

ابتدا به عددگر نگاه می کنیم و با بالاترین توان آن را پیدا می کنیم: بالاترین درجه در صورتگر دو است.

اکنون به مخرج نگاه می کنیم و همچنین در بالاترین توان پیدا می کنیم: بالاترین توان مخرج دو است.

سپس بالاترین توان صورت و مخرج را انتخاب می کنیم: در این مثال، آنها یکسان و برابر با دو هستند.

بنابراین، روش حل به شرح زیر است: به منظور کشف عدم قطعیتلازم است که صورت و مخرج را بر تقسیم کنیمدر مقطع ارشد

صورت و مخرج را تقسیم بر

جواب همین است، نه بی نهایت.

چه چیزی اساساً در طراحی راه حل مهم است؟

ابتدا عدم قطعیت را در صورت وجود نشان می دهیم.

ثانیاً، توصیه می شود که راه حل را برای توضیحات میانی قطع کنید. من معمولا از یک علامت استفاده می کنم، هیچ معنای ریاضی ندارد، اما به این معنی است که راه حل برای یک توضیح میانی قطع شده است.

ثالثاً، در حد مطلوب است که مشخص شود چه چیزی و کجا تلاش می کند. هنگامی که کار با دست کامل می شود، راحت تر است که آن را به این صورت انجام دهید: بهتر است از یک مداد ساده برای علامت گذاری استفاده کنید.

البته، شما نمی توانید هیچ کاری از این کار انجام دهید، اما پس از آن، شاید معلم کاستی های موجود در راه حل را یادداشت کند یا شروع به پرسیدن سوالات اضافی در مورد تکلیف کند. آیا به آن نیاز دارید؟

مثال 5

حد را پیدا کنید باز هم در صورت و مخرج در بالاترین توان می یابیم: حداکثر درجه در صورت: 3 حداکثر درجه در مخرج: 4 انتخاب کنید بهترینمقدار، در این مورد چهار. طبق الگوریتم ما، برای افشای عدم قطعیت، صورت و مخرج را بر تقسیم می کنیم. طراحی کامل تکلیف ممکن است به شکل زیر باشد:

مثال 6

حد را پیدا کنید حداکثر درجه "x" در صورت: 2 حداکثر درجه "x" در مخرج: 1 (می توان آن را به صورت نوشت) برای آشکار کردن عدم قطعیت، صورت و مخرج را بر تقسیم کنید. یک راه حل تمیز ممکن است به شکل زیر باشد:

صورت و مخرج را تقسیم بر

ضبط به معنای تقسیم بر صفر نیست (شما نمی توانید بر صفر تقسیم کنید)، بلکه تقسیم بر یک عدد بی نهایت کوچک است.

بنابراین، هنگام افشای عدم قطعیت گونه، می توانیم دریافت کنیم عدد محدود، صفر یا بی نهایت.

تمرین 20

شغل شماره 1

راه حل:اگر به جای متغیر، مقدار 7 را که به آن تمایل دارد قرار دهیم، عدم قطعیت فرم را دریافت می کنیم، سپس

شغل شماره 2موضوع: افشای عدم قطعیت صفر تا صفر

راه حل:اگر به جای متغیر، مقدار 0 را که به آن تمایل دارد قرار دهیم، عدم قطعیت فرم را دریافت می کنیم، سپس

شغل شماره 3موضوع: افشای عدم قطعیت صفر تا صفر

راه حل:اگر به جای متغیر، مقدار 6 را که به آن تمایل دارد قرار دهیم، عدم قطعیت شکل را دریافت می کنیم، سپس

شغل شماره 4

راه حل:زیرا و

شغل شماره 5موضوع: افشای عدم قطعیت شکل "بی نهایت تا بی نهایت"

راه حل:زیرا و سپس شکل عدم قطعیت وجود دارد. برای آشکار کردن آن، باید هر جمله صورت و مخرج را بر تقسیم کنید. سپس، دانستن اینکه ما دریافت خواهیم کرد:

کار مستقل 20

شغل شماره 1موضوع: افشای عدم قطعیت صفر تا صفر

شغل شماره 2موضوع: افشای عدم قطعیت صفر تا صفر

شغل شماره 3موضوع: افشای عدم قطعیت صفر تا صفر

شغل شماره 4موضوع: افشای عدم قطعیت شکل "بی نهایت تا بی نهایت"

شغل شماره 5موضوع: افشای عدم قطعیت شکل "بی نهایت تا بی نهایت"محدودیت عملکرد برابر ...

شغل شماره 6موضوع: افشای عدم قطعیت شکل "بی نهایت تا بی نهایت"

روش های حل حدود عدم قطعیت ها
ترتیب رشد تابع. روش جایگزینی

مثال 4

حد را پیدا کنید

این یک مثال ساده تر برای راه حلی است که خودتان انجام دهید. در مثال پیشنهادی، مجدداً عدم قطعیت (از مرتبه رشد بالاتر از ریشه) وجود دارد.

اگر "x" به "منهای بی نهایت" تمایل دارد

شبح «منهای بی نهایت» مدت هاست که در این مقاله آمده است. حدودی را با چند جمله ای در نظر بگیرید که در آن. اصول و روش های حل دقیقاً مانند قسمت اول درس خواهد بود، به استثنای تعدادی از تفاوت های ظریف.

4 تراشه را در نظر بگیرید که برای حل کارهای عملی مورد نیاز است:

1) حد را محاسبه کنید

مقدار حد فقط به مدت بستگی دارد، زیرا بالاترین ترتیب رشد را دارد. اگر پس از آن مدول بی نهایت بزرگعدد منفی به توان زوج، در این مورد - در چهارم، برابر با "به علاوه بی نهایت":. ثابت ("دو") مثبت، از همین رو:

2) حد را محاسبه کنید

اینجا دوباره مدرک ارشد زوج، از همین رو: . اما در مقابل "منهای" ( منفیثابت -1)، بنابراین:

3) حد را محاسبه کنید

مقدار حد فقط به این بستگی دارد. همانطور که از مدرسه به یاد دارید، بنابراین "منهای" از زیر درجه فرد "بیرون می پرد". مدول بی نهایت بزرگعدد منفی به توان فردبرابر است با "منهای بی نهایت"، در این مورد:.
ثابت ("چهار") مثبت، به معنای:

4) حد را محاسبه کنید

اولین پسر روستا دوباره دارد فرددرجه، علاوه بر این، در سینه منفیثابت که به این معنی است:
.

مثال 5

حد را پیدا کنید

با استفاده از نکات فوق به این نتیجه می رسیم که عدم قطعیت وجود دارد. صورت و مخرج از نظر رشد یکسان هستند، به این معنی که در حد یک عدد متناهی به دست می آید. بیایید پاسخ را پیدا کنیم و همه سرخ شده را دور بریزیم:

راه حل بی اهمیت است:

مثال 6

حد را پیدا کنید

این یک مثال برای راه حلی است که خودتان انجام دهید. حل کامل و پاسخ در پایان آموزش.

و اکنون، شاید ظریف ترین موارد:

مثال 7

حد را پیدا کنید

با توجه به اصطلاحات پیشرو، به این نتیجه می رسیم که عدم قطعیت وجود دارد. صورت‌گر دارای مرتبه رشد بالاتری نسبت به مخرج است، بنابراین بلافاصله می‌توانید بگویید که حد بی‌نهایت است. اما کدام بی نهایت، مثبت یا منفی؟ تکنیک یکسان است - در صورت و مخرج از شر چیزهای کوچک خلاص می شویم:

ما تصمیم گرفتیم:

صورت و مخرج را تقسیم بر

مثال 15

حد را پیدا کنید

این یک مثال برای راه حلی است که خودتان انجام دهید. یک مثال تقریبی از اتمام در پایان درس.

چند مثال جالب دیگر در مورد جایگزینی متغیر:

مثال 16

حد را پیدا کنید

هنگام جایگزینی یک واحد در حد، عدم قطعیت به دست می آید. جایگزینی متغیر در حال حاضر واضح است، اما ابتدا مماس را با استفاده از فرمول تبدیل می کنیم. به راستی چرا به مماس نیاز داریم؟

توجه داشته باشید که، بنابراین. اگر کاملاً واضح نیست، به مقادیر سینوسی در آن نگاه کنید جدول مثلثاتی... بنابراین، ما بلافاصله از شر ضریب خلاص می شویم، علاوه بر این، عدم قطعیت آشناتر 0: 0 را دریافت می کنیم. همچنین اگر حد به صفر گرایش داشته باشد خوب است.

بیایید جایگزین کنیم:

اگر پس از آن

در زیر کسینوس "x" داریم که باید از طریق "te" نیز بیان شود.
از جایگزینی بیان می کنیم:.

راه حل را کامل می کنیم:

(1) ما تعویض را انجام می دهیم

(2) براکت های زیر کسینوس را باز کنید.

(4) سازماندهی اولین حد فوق العاده، صورت مصنوعی را در و متقابل ضرب کنید.

تکلیف برای راه حل مستقل:

مثال 17

حد را پیدا کنید

حل کامل و پاسخ در پایان آموزش.

اینها در کلاس آنها کارهای سختی نبودند، در عمل همه چیز می تواند بدتر باشد، و علاوه بر این فرمول های کاهش، باید از انواع مختلف استفاده کنید فرمول های مثلثاتیو همچنین ترفندهای دیگر. در مقاله محدودیت های دشوار، من چند مثال واقعی را از هم جدا کردم =)

در آستانه تعطیلات، اجازه دهید در نهایت وضعیت را با یک عدم اطمینان گسترده تر روشن کنیم:

حذف عدم قطعیت "یک تا درجه بی نهایت"

این عدم قطعیت "در خدمت" است دومین محدودیت فوق العادهو در قسمت دوم آن درس، نمونه‌های استاندارد راه‌حل‌هایی را که در بیشتر موارد در عمل با آن‌ها مواجه می‌شویم، با جزئیات کامل بررسی کردیم. اکنون تصویر با غرفه داران تکمیل می شود، علاوه بر این، وظایف نهایی درس به محدودیت ها - "ترفند" اختصاص می یابد، که در آن به نظر می رسد که لازم است محدودیت فوق العاده دوم را اعمال کنید، اگرچه این در این مورد نیست. همه موارد

نقطه ضعف دو فرمول کاری حد قابل توجه 2 این است که آرگومان باید به سمت "بعلاوه بی نهایت" یا صفر گرایش داشته باشد. اما اگر آرگومان به عدد دیگری گرایش پیدا کند، چه؟

یک فرمول جهانی به کمک می آید (که در واقع نتیجه دومین محدودیت قابل توجه است):

عدم قطعیت را می توان با فرمول حذف کرد:

در جایی مثل قبلا توضیح داده شد که پرانتز به چه معناست. چیز خاصی نیست، براکت ها مانند براکت هستند. آنها معمولاً برای واضح تر کردن نمادهای ریاضی استفاده می شوند.

بیایید نکات اساسی فرمول را برجسته کنیم:

1) هست فقط در مورد عدم قطعیت و هیچ چیز دیگری.

2) آرگومان "x" ممکن است تمایل داشته باشد مقدار دلخواه(و نه تنها به صفر یا، به ویژه، به "منهای بی نهایت" یا به هریک عدد محدود

با استفاده از این فرمول می توانید تمام مثال های درس را حل کنید. محدودیت های شگفت انگیزکه به 2مین حد قابل توجه تعلق دارند. به عنوان مثال، بیایید حد را محاسبه کنیم:

در این مورد ، و با فرمول :

درست است، من به شما توصیه نمی کنم که این کار را انجام دهید، در سنت هنوز از طرح "معمول" راه حل استفاده کنید، اگر بتوان آن را اعمال کرد. ولی استفاده از یک فرمول برای بررسی بسیار راحت استنمونه های "کلاسیک" در حد قابل توجه 2.