फलन का अवकलज बहुत दूर नहीं जाता है, और L'Hôpital के नियमों के मामले में, यह ठीक उसी दिशा में गिरता है जिस दिशा में मूल फलन होता है। यह परिस्थिति फॉर्म 0/0 या / की अनिश्चितताओं और गणना करते समय उत्पन्न होने वाली कुछ अन्य अनिश्चितताओं का खुलासा करने में मदद करती है। सीमादो अतिसूक्ष्म या अपरिमित रूप से बड़े फलनों का अनुपात। इस नियम की मदद से गणना बहुत सरल है (वास्तव में, दो नियम और उनके लिए नोट्स):
जैसा कि ऊपर दिए गए सूत्र से पता चलता है, दो अनंत या असीम रूप से बड़े कार्यों के अनुपात की सीमा की गणना करते समय, दो कार्यों के अनुपात की सीमा को उनके अनुपात की सीमा से बदला जा सकता है डेरिवेटिवऔर इस प्रकार एक निश्चित परिणाम प्राप्त करें।
आइए L'Hôpital के नियमों के अधिक सटीक सूत्रीकरण की ओर बढ़ते हैं।
दो अतिसूक्ष्म मात्राओं की सीमा के मामले के लिए L'Hpital का नियम... कार्यों को करने दें एफ(एक्स) तथा जी(एक्स ए... और बिल्कुल सही ए एकिसी फ़ंक्शन का व्युत्पन्न जी(एक्स) शून्य के बराबर नहीं है ( जी"(एक्स एएक दूसरे के बराबर और शून्य के बराबर हैं:
.
दो अपरिमित रूप से बड़ी मात्राओं की सीमा के मामले के लिए L'Hôpital का नियम... कार्यों को करने दें एफ(एक्स) तथा जी(एक्स) बिंदु के कुछ पड़ोस में डेरिवेटिव (यानी, अलग-अलग) हैं ए... और बिल्कुल सही एउनके पास डेरिवेटिव हो सकता है या नहीं भी हो सकता है। इसके अलावा, बिंदु के आसपास के क्षेत्र में एकिसी फ़ंक्शन का व्युत्पन्न जी(एक्स) शून्य के बराबर नहीं है ( जी"(एक्स) 0) और x के रूप में इन कार्यों की सीमाएं बिंदु पर फ़ंक्शन के मान की ओर प्रवृत्त होती हैं एएक दूसरे के बराबर और अनंत के बराबर हैं:
.
फिर इन कार्यों के अनुपात की सीमा उनके डेरिवेटिव के अनुपात की सीमा के बराबर है:
दूसरे शब्दों में, फॉर्म 0/0 या ∞ / की अनिश्चितताओं के लिए, दो कार्यों के अनुपात की सीमा उनके डेरिवेटिव के अनुपात की सीमा के बराबर होती है, यदि बाद वाला मौजूद है (परिमित, जो बराबर है) निश्चित संख्या, या अनंत, यानी अनंत के बराबर)।
टिप्पणियां.
1. L'Hpital के नियम तब भी लागू होते हैं जब फंक्शन एफ(एक्स) तथा जी(एक्स) के लिए परिभाषित नहीं हैं एक्स = ए.
2. यदि, फलनों के व्युत्पन्नों के अनुपात की सीमा की गणना करते समय एफ(एक्स) तथा जी(एक्स) फिर से हम फॉर्म 0/0 या / की अनिश्चितता पर पहुंचते हैं, तो L'Hôpital के नियमों को कई बार (कम से कम दो बार) लागू किया जाना चाहिए।
3. L'Hôpital के नियम तब भी लागू होते हैं जब फलन (x) का तर्क परिमित संख्या की ओर नहीं जाता है ए, और अनंत तक ( एक्स → ∞).
अन्य प्रकार की अनिश्चितताओं को भी 0/0 और / ∞ प्रकार की अनिश्चितताओं में कम किया जा सकता है।
"शून्य से विभाजित शून्य" और "अनंत से विभाजित अनंत" प्रकारों की अनिश्चितताओं का प्रकटीकरण
उदाहरण 1।
एक्स= 2 परिणाम 0/0 के रूप में अनिश्चितता का कारण बनता है। इसलिए, प्रत्येक फ़ंक्शन का व्युत्पन्न और हम प्राप्त करते हैं
बहुपद के व्युत्पन्न की गणना अंश में और हर में की जाती है - एक जटिल लॉगरिदमिक फ़ंक्शन का व्युत्पन्न... अंतिम बराबर चिह्न से पहले, सामान्य सीमा, x के बजाय दो को प्रतिस्थापित करना।
उदाहरण 2। L'Hôpital के नियम का उपयोग करके दो कार्यों के अनुपात की सीमा की गणना करें:
समाधान। किसी दिए गए फ़ंक्शन में मान का प्रतिस्थापन एक्स
उदाहरण 3. L'Hôpital के नियम का उपयोग करके दो कार्यों के अनुपात की सीमा की गणना करें:
समाधान। किसी दिए गए फ़ंक्शन में मान का प्रतिस्थापन एक्स= 0 परिणाम 0/0 के रूप में अनिश्चितता का कारण बनता है। इसलिए, हम अंश और हर में कार्यों के डेरिवेटिव की गणना करते हैं और प्राप्त करते हैं:
उदाहरण 4.गणना
समाधान। दिए गए फ़ंक्शन में x मान को प्लस इनफिनिटी के बराबर करने से / के रूप की अनिश्चितता होती है। इसलिए, हम L'Hôpital का नियम लागू करते हैं:
टिप्पणी। आइए हम उन उदाहरणों की ओर मुड़ें जिनमें L'Hôpital के नियम को दो बार लागू करना पड़ता है, यानी दूसरे डेरिवेटिव के अनुपात की सीमा तक आने के लिए, क्योंकि पहले डेरिवेटिव के अनुपात की सीमा फॉर्म 0 की अनिश्चितता है। /0 या / .
"शून्य गुणा अनंत" प्रपत्र की अनिश्चितताओं का प्रकटीकरण
उदाहरण 12.गणना
.
समाधान। हम पाते हैं
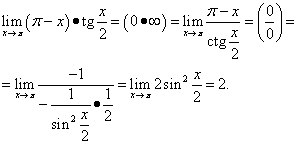
यह उदाहरण त्रिकोणमितीय पहचान का उपयोग करता है।
"शून्य की शक्ति के लिए शून्य", "शून्य की शक्ति के लिए अनंत" और "अनंत की शक्ति के लिए एक" प्रकार की अनिश्चितताओं का प्रकटीकरण
फॉर्म की अनिश्चितता, या आमतौर पर फॉर्म के एक फ़ंक्शन के लॉगरिदम का उपयोग करके 0/0 या ∞ / के रूप में कम हो जाती है
व्यंजक की सीमा की गणना करने के लिए, लघुगणकीय पहचान का उपयोग करना चाहिए, जिसका एक विशेष मामला लघुगणक की संपत्ति है 
.
लॉगरिदमिक पहचान और फ़ंक्शन की निरंतरता संपत्ति (सीमा चिह्न से आगे जाने के लिए) का उपयोग करके, सीमा की गणना निम्नानुसार की जानी चाहिए:
अलग से, आपको घातांक में अभिव्यक्ति की सीमा का पता लगाना चाहिए और निर्माण करना चाहिए इडिग्री तक पाया।
उदाहरण 13.
समाधान। हम पाते हैं
.
.
उदाहरण 14. L'Hpital's नियम का उपयोग करके गणना करें
समाधान। हम पाते हैं
हम घातांक में व्यंजक की सीमा की गणना करते हैं
.
.
उदाहरण 15. L'Hpital's नियम का उपयोग करके गणना करें
प्रकार और प्रकार की अनिश्चितताएं सबसे आम अनिश्चितताएं हैं जिन्हें सीमाओं को हल करते समय प्रकट करने की आवश्यकता होती है।
छात्रों के सामने आने वाले अधिकांश कार्यों में बस ऐसी ही अनिश्चितताएँ होती हैं। उन्हें प्रकट करने के लिए, या, अधिक सटीक रूप से, अस्पष्टताओं से बचने के लिए, सीमा चिह्न के तहत अभिव्यक्ति के रूप को बदलने के लिए कई कृत्रिम तरीके हैं। ये तकनीकें इस प्रकार हैं: चर की उच्चतम शक्ति द्वारा अंश और हर का पद-दर-भाग विभाजन, द्विघात समीकरणों और संक्षिप्त गुणन सूत्रों के समाधान का उपयोग करके बाद में कमी के लिए संयुग्म अभिव्यक्ति और गुणन द्वारा गुणा।
प्रजातियों की अनिश्चितता
उदाहरण 1।
एन 2 के बराबर है। इसलिए, हम अंश और हर को पद से विभाजित करते हैं:
.
अभिव्यक्ति के दाईं ओर टिप्पणी करें। तीर और संख्याएँ इंगित करती हैं कि के बजाय प्रतिस्थापन के बाद भिन्न क्या करते हैं एनअनंत मूल्य। यहाँ, उदाहरण 2 के रूप में, डिग्री एनअंश की तुलना में हर में अधिक, जिसके परिणामस्वरूप पूरा अंश एक असीम रूप से छोटे मान या "सुपर-स्मॉल नंबर" की ओर जाता है।
हमें उत्तर मिलता है: अनंत की ओर झुकाव वाले चर के साथ इस फ़ंक्शन की सीमा के बराबर है।
उदाहरण 2। .
समाधान। यहाँ चर की उच्चतम शक्ति एक्स 1 के बराबर है। इसलिए, हम अंश और हर को पद से विभाजित करते हैं एक्स:
.
समाधान के पाठ्यक्रम पर टिप्पणी। अंश में हम तीसरी डिग्री की जड़ के नीचे "x" चलाते हैं, और इसलिए कि इसकी प्रारंभिक डिग्री (1) अपरिवर्तित रहती है, हम इसे मूल के समान डिग्री प्रदान करते हैं, अर्थात 3. कोई और तीर नहीं हैं और इस प्रविष्टि में अतिरिक्त संख्याएं, इसलिए मानसिक रूप से प्रयास करें, लेकिन पिछले उदाहरण के अनुरूप, यह निर्धारित करें कि अंश और हर में अभिव्यक्ति "x" के लिए अनंत को प्रतिस्थापित करने के बाद क्या प्रयास कर रही है।
हमें उत्तर मिला: अनंत की ओर झुकाव वाले चर के साथ इस फ़ंक्शन की सीमा शून्य के बराबर है।
प्रजातियों की अनिश्चितता
उदाहरण 3.अनिश्चितता को उजागर करें और एक सीमा खोजें।
समाधान। अंश घनों के बीच का अंतर है। आइए स्कूल गणित पाठ्यक्रम से संक्षिप्त गुणन के सूत्र का उपयोग करके इसका गुणनखंड करें:
हर एक द्विघात त्रिपद है, जिसे हम द्विघात समीकरण (एक बार फिर द्विघात समीकरणों को हल करने के लिए एक संदर्भ) को हल करके निकालते हैं:
आइए परिवर्तनों के परिणामस्वरूप प्राप्त अभिव्यक्ति को लिखें और फ़ंक्शन की सीमा ज्ञात करें:
उदाहरण 4.अनिश्चितता को उजागर करें और सीमा का पता लगाएं
समाधान। भागफल सीमा प्रमेय यहाँ लागू नहीं है, क्योंकि
इसलिए, हम भिन्न को समान रूप से बदलते हैं: द्विपद संयुग्म द्वारा अंश और हर को हर से गुणा करना, और इसे रद्द करना एक्स+1। प्रमेय 1 के उपफल के अनुसार, हमें एक व्यंजक प्राप्त होता है, जिसे हल करने पर हमें वांछित सीमा प्राप्त होती है:
उदाहरण 5.अनिश्चितता को उजागर करें और सीमा का पता लगाएं
समाधान। प्रत्यक्ष मूल्य प्रतिस्थापन एक्स= 0 दिए गए फलन के परिणाम स्वरूप 0/0 की अनिश्चितता उत्पन्न होती है। इसे प्रकट करने के लिए, हम समान परिवर्तन करते हैं और परिणामस्वरूप वांछित सीमा प्राप्त करते हैं: 
उदाहरण 6.गणना 
समाधान:हम सीमा पर प्रमेयों का उपयोग करते हैं
उत्तर: 11
उदाहरण 7.गणना 
समाधान:इस उदाहरण में, अंश और हर की सीमाएँ 0 हैं:
; 
... हमने प्राप्त किया है, इसलिए, भागफल की सीमा पर प्रमेय लागू नहीं किया जा सकता है।
आइए हम अंश और हर को शून्य की ओर प्रवृत्त एक सामान्य गुणनखंड द्वारा भिन्न को रद्द करने के लिए निकालें, और इसलिए, प्रमेय 3 के अनुप्रयोग को संभव बनाने के लिए।
हम अंश में वर्ग त्रिपद को सूत्र द्वारा विस्तारित करते हैं, जहाँ x 1 और x 2 त्रिपद के मूल हैं। गुणनखंडित और निरूपित करके भिन्न को (x-2) से रद्द करें, फिर प्रमेय 3 लागू करें।
उत्तर:
उदाहरण 8.गणना
समाधान:पर, अंश और हर अनंत की ओर प्रवृत्त होते हैं; इसलिए, प्रमेय 3 के प्रत्यक्ष अनुप्रयोग के साथ, हमें एक ऐसा व्यंजक प्राप्त होता है जो अनिश्चितता का प्रतिनिधित्व करता है। इस तरह की अस्पष्टता से छुटकारा पाने के लिए, अंश और हर को तर्क के उच्चतम अंश से विभाजित करें। इस उदाहरण में, आपको द्वारा विभाजित करने की आवश्यकता है एक्स:
उत्तर:
उदाहरण 9.गणना 
समाधान: एक्स 3:
उत्तर: 2
उदाहरण 10.गणना 
समाधान:जब अंश और हर अनंत की ओर प्रवृत्त होते हैं। अंश और हर को तर्क की उच्चतम डिग्री से विभाजित करें, अर्थात। एक्स 5:
= 
भिन्न का अंश 1 की ओर प्रवृत्त होता है, हर 0 की ओर, इसलिए भिन्न अनंत की ओर प्रवृत्त होता है।
उत्तर:
उदाहरण 11.गणना
समाधान:जब अंश और हर अनंत की ओर प्रवृत्त होते हैं। अंश और हर को तर्क की उच्चतम डिग्री से विभाजित करें, अर्थात। एक्स 7:
उत्तर: 0
व्युत्पन्न।
फलन का व्युत्पन्न y = f (x) तर्क x . के संबंध मेंजब तर्क की वृद्धि शून्य हो जाती है, तो तर्क x के वेतन वृद्धि x से इसके वेतन वृद्धि y के अनुपात की सीमा होती है। यदि यह सीमा परिमित है, तो फलन वाई = एफ (एक्स)बिंदु x पर अवकलनीय कहलाता है। यदि यह सीमा मौजूद है, तो वे कहते हैं कि फलन वाई = एफ (एक्स)बिंदु x पर अनंत अवकलज है।
बुनियादी प्राथमिक कार्यों के व्युत्पन्न:
1. (स्थिरांक) = 0 9. 
3. 11. 
4. 
12. 
5. 13. 
6. 
14. 
भेदभाव नियम:
ए) 
वी) 
उदाहरण 1।किसी फ़ंक्शन के व्युत्पन्न का पता लगाएं 
समाधान:यदि दूसरे पद का व्युत्पन्न भिन्न के विभेदन के नियम के अनुसार पाया जाता है, तो पहला पद एक जटिल कार्य है, जिसका व्युत्पन्न सूत्र द्वारा पाया जाता है:
, कहाँ पे 
, फिर
हल करते समय सूत्रों का उपयोग किया गया: 1,2,10, ए, सी, डी।
उत्तर:
उदाहरण 21.किसी फ़ंक्शन के व्युत्पन्न का पता लगाएं 
समाधान:दोनों पद जटिल फलन हैं, जहां पहले के लिए, और दूसरे के लिए, तब
उत्तर: 
व्युत्पन्न अनुप्रयोग।
1. गति और त्वरण
मान लें कि फ़ंक्शन s (t) वर्णन करता है पदसमय t पर एक निश्चित समन्वय प्रणाली में वस्तु। तब फ़ंक्शन s (t) का पहला व्युत्पन्न तात्कालिक है स्पीडवस्तु:
वी = एस = एफ ′ (टी)
फ़ंक्शन s (t) का दूसरा व्युत्पन्न तात्कालिक है त्वरणवस्तु:
डब्ल्यू = वी ′ = एस = एफ ′ (टी)
2. स्पर्शरेखा समीकरण
y - y0 = f ′ (x0) (x - x0),
जहां (x0, y0) स्पर्शरेखा के बिंदु के निर्देशांक हैं, f (x0) स्पर्शरेखा के बिंदु पर फ़ंक्शन f (x) के व्युत्पन्न का मान है।
3. सामान्य समीकरण
y - y0 = −1f ′ (x0) (x - x0),
जहाँ (x0, y0) उस बिंदु के निर्देशांक हैं जिस पर अभिलंब खींचा जाता है, f (x0) इस बिंदु पर फलन f (x) के अवकलज का मान है।
4. बढ़ते और घटते कार्य
यदि f (x0)> 0, तो बिंदु x0 पर फलन बढ़ता है। नीचे दिए गए चित्र में, फलन x . के रूप में बढ़ रहा है
अगर एफ (x0)<0, то функция убывает в точке x0 (интервал x1
5. एक समारोह के स्थानीय एक्स्ट्रेमा
फलन f (x) में है स्थानीय अधिकतमबिंदु X1 पर यदि बिंदु X1 का एक पड़ोस मौजूद है जैसे कि असमानता f (x1) f (x) इस पड़ोस से सभी x के लिए है।
इसी प्रकार, फलन f (x) में है स्थानीय न्यूनतमबिंदु x2 पर यदि बिंदु x2 का एक पड़ोस मौजूद है जैसे कि इस पड़ोस से सभी x के लिए असमानता f (x2) f (x) है।
6. महत्वपूर्ण बिंदु
बिंदु x0 है महत्वपूर्ण बिंदुफलन f (x) यदि इसमें अवकलज f (x0) शून्य के बराबर है या मौजूद नहीं है।
7. एक चरम के अस्तित्व का पहला पर्याप्त संकेतक
यदि फलन f (x) किसी अंतराल (a, x1] में सभी x के लिए (f (x)> 0) बढ़ता है और घटता है (f (x))<0) для всех x в интервале и возрастает (f′(x)>0) अंतराल से सभी x के लिए ^ \ infty $ और $ ^ \ infty $।
साथ ही, इस तरह की अनिश्चितताओं को घातांक फ़ंक्शन के लघुगणक का उपयोग करके प्रकट किया जा सकता है, लेकिन यह एक अलग समाधान विधि है, जिसे एक अन्य लेख में शामिल किया जाएगा।
सूत्र और परिणाम
सूत्रदूसरी उल्लेखनीय सीमा इस प्रकार लिखी गई है: $$ \ lim_ (x \ to \ infty) \ bigg (1+ \ frac (1) (x) \ bigg) ^ x = e, \ text (जहाँ) e \ लगभग 2.718 $$
सूत्र का तात्पर्य है परिणाम, जो सीमा के साथ उदाहरणों को हल करने के लिए उपयोग करने के लिए बहुत सुविधाजनक हैं: $$ \ lim_ (x \ to \ infty) \ bigg (1 + \ frac (k) (x) \ bigg) ^ x = e ^ k, \ text ( जहां) k \ in \ mathbb (R) $$ $$ \ lim_ (x \ to \ infty) \ bigg (1 + \ frac (1) (f (x)) \ bigg) ^ (f (x)) = ई $$ $$ \ lim_ (x \ to 0) \ bigg (1 + x \ bigg) ^ \ frac (1) (x) = e $$
यह ध्यान देने योग्य है कि दूसरी उल्लेखनीय सीमा हमेशा घातीय फ़ंक्शन पर लागू नहीं की जा सकती है, लेकिन केवल उन मामलों में जहां आधार एकता की ओर जाता है। इसके लिए पहले मन में आधार सीमा की गणना की जाती है और फिर निष्कर्ष निकाला जाता है। यह सब नमूना समाधान में शामिल किया जाएगा।
समाधान के उदाहरण
आइए प्रत्यक्ष सूत्र और उसके परिणामों का उपयोग करके समाधानों के उदाहरणों पर विचार करें। हम उन मामलों का भी विश्लेषण करेंगे जिनमें सूत्र की आवश्यकता नहीं है। केवल तैयार उत्तर लिखने के लिए पर्याप्त है।
| उदाहरण 1 |
| सीमा ज्ञात कीजिए $ \ lim_ (x \ to \ infty) \ bigg (\ frac (x + 4) (x + 3) \ bigg) ^ (x + 3) $ |
| समाधान |
|
आइए अनंत को सीमा में बदलें और अनिश्चितता को देखें: $$ \ lim_ (x \ to \ infty) \ bigg (\ frac (x + 4) (x + 3) \ bigg) ^ (x + 3) = \ bigg (\ frac (\ infty) (\ infty) \ bigg) ^ \ infty $$ आधार की सीमा ज्ञात कीजिए: $$ \ lim_ (x \ to \ infty) \ frac (x + 4) (x + 3) = \ lim_ (x \ to \ infty) \ frac (x (1+ \ frac ( 4) (एक्स))) (एक्स (1+ \ फ्रैक (3) (एक्स))) = 1 $$ हमें एक के बराबर आधार मिला, जिसका अर्थ है कि दूसरी उल्लेखनीय सीमा पहले से ही लागू की जा सकती है। ऐसा करने के लिए, हम फ़ंक्शन के आधार को घटाकर और एक जोड़कर सूत्र में फिट करते हैं: $$ \ lim_ (x \ to \ infty) \ bigg (1 + \ frac (x + 4) (x + 3) - 1 \ bigg) ^ (x + 3) = \ lim_ (x \ to \ infty) \ बिग (1 + \ फ़्रेक (1) (x + 3) \ bigg) ^ (x + 3) = $$ हम दूसरे परिणाम को देखते हैं और उत्तर लिखते हैं: $$ \ lim_ (x \ to \ infty) \ bigg (1 + \ frac (1) (x + 3) \ bigg) ^ (x + 3) = e $$ यदि आप अपनी समस्या का समाधान नहीं कर सकते हैं, तो हमें भेजें। हम एक विस्तृत समाधान प्रदान करेंगे। आप गणना के पाठ्यक्रम से खुद को परिचित करने और जानकारी प्राप्त करने में सक्षम होंगे। इससे आपको अपने शिक्षक से समय पर क्रेडिट प्राप्त करने में मदद मिलेगी! |
| उत्तर |
| $$ \ lim_ (x \ to \ infty) \ bigg (1 + \ frac (1) (x + 3) \ bigg) ^ (x + 3) = e $$ |
| उदाहरण 4 |
| हल सीमा $ \ lim_ (x \ to \ infty) \ bigg (\ frac (3x ^ 2 + 4) (3x ^ 2-2) \ bigg) ^ (3x) $ |
| समाधान |
|
हम आधार की सीमा ज्ञात करते हैं और देखते हैं कि $ \ lim_ (x \ to \ infty) \ frac (3x ^ 2 + 4) (3x ^ 2-2) = 1 $, इसलिए दूसरी अद्भुत सीमा लागू की जा सकती है। मानक रूप से, योजना के अनुसार, हम डिग्री के आधार में से एक को जोड़ते और घटाते हैं: $$ \ lim_ (x \ to \ infty) \ bigg (1+ \ frac (3x ^ 2 + 4) (3x ^ 2-2) -1 \ bigg) ^ (3x) = \ lim_ (x \ से \ infty) ) \ bigg (1+ \ frac (6) (3x ^ 2-2) \ bigg) ^ (3x) = $$ हम भिन्न को दूसरी टिप्पणी के सूत्र में फिट करते हैं। सीमा: $$ = \ lim_ (x \ to \ infty) \ bigg (1+ \ frac (1) (\ frac (3x ^ 2-2) (6)) \ bigg) ^ (3x) = $$ अब डिग्री एडजस्ट करते हैं। घात, आधार $\ frac (3x ^ 2-2) (6) $ के हर के बराबर एक अंश होना चाहिए। ऐसा करने के लिए, डिग्री को इसके द्वारा गुणा और विभाजित करें, और हल करना जारी रखें: $$ = \ lim_ (x \ to \ infty) \ bigg (1+ \ frac (1) (\ frac (3x ^ 2-2) (6)) \ bigg) ^ (\ frac (3x ^ 2-2) (6) \ cdot \ frac (6) (3x ^ 2-2) \ cdot 3x) = \ lim_ (x \ to \ infty) e ^ (\ frac (18x) (3x ^ 2-2)) = $$ $ e $ पर डिग्री में स्थित सीमा है: $ \ lim_ (x \ to \ infty) \ frac (18x) (3x ^ 2-2) = 0 $। इसलिए, समाधान जारी रखते हुए, हमारे पास है: |
| उत्तर |
| $$ \ lim_ (x \ to \ infty) \ bigg (\ frac (3x ^ 2 + 4) (3x ^ 2-2) \ bigg) ^ (3x) = 1 $$ |
आइए हम उन मामलों की जांच करें जब समस्या दूसरी उल्लेखनीय सीमा के समान है, लेकिन इसके बिना इसे हल किया जा सकता है।
लेख में: "दूसरी उल्लेखनीय सीमा: समाधान के उदाहरण" सूत्र, उसके परिणामों का विश्लेषण किया गया था, और इस विषय पर लगातार प्रकार की समस्याओं को दिया गया था।
विचार 20
20.1 अनिश्चितता प्रकटीकरण
उदाहरण 1
सीमा को हल करें 
सबसे पहले, आइए भिन्न में -1 को प्रतिस्थापित करने का प्रयास करें: 
इस मामले में, तथाकथित अनिश्चितता प्राप्त की जाती है।
सामान्य नियम:यदि अंश और हर में बहुपद हैं, और प्रपत्र की अनिश्चितताएं हैं, तो इसके प्रकटीकरण के लिए आपको अंश और हर का गुणनखंड करना होगा.
ऐसा करने के लिए, सबसे अधिक बार आपको द्विघात समीकरण को हल करने और / या संक्षिप्त गुणन सूत्रों का उपयोग करने की आवश्यकता होती है।
अंश का गुणनखंड करें। 
उदाहरण 2
सीमा की गणना करें 
आइए अंश और हर का गुणनखंड करें।
अंश भाजक: 
,
संयुग्मी व्यंजक द्वारा अंश और हर को गुणा करने की विधि
हम फॉर्म की अनिश्चितता पर विचार करना जारी रखते हैं
अगले प्रकार की सीमाएँ पिछले प्रकार के समान हैं। केवल एक चीज, बहुपदों के अलावा, हम जड़ें जोड़ेंगे।
उदाहरण 3
सीमा का पता लगाएं 
संयुग्मी व्यंजक द्वारा अंश और हर को गुणा करें।
20.2 अनिश्चितता प्रकटीकरण
अब हम सीमाओं के एक समूह पर विचार करेंगे, जब और फलन एक भिन्न हो, जिसके अंश और हर में बहुपद हों
उदाहरण 4
सीमा की गणना करें 
हमारे नियम के अनुसार, हम फलन में अनंत को प्रतिस्थापित करने का प्रयास करेंगे। हमें सबसे ऊपर क्या मिलता है? अनंतता। और नीचे क्या होता है? अनंत भी। तो हमारे पास प्रजातियों की तथाकथित अनिश्चितता है। कोई ऐसा सोचेगा, और उत्तर तैयार है, लेकिन सामान्य स्थिति में ऐसा बिल्कुल नहीं है, और आपको कुछ समाधान तकनीक लागू करने की आवश्यकता है, जिस पर अब हम विचार करेंगे।
किसी दिए गए प्रकार की सीमाओं को कैसे हल करें?
सबसे पहले, हम अंश को देखते हैं और उच्चतम घात में पाते हैं: 
अंश में उच्चतम डिग्री दो है।
अब हम हर को देखते हैं और उच्चतम घात में भी पाते हैं: 
हर की उच्चतम शक्ति दो है।
फिर हम अंश और हर की उच्चतम शक्ति चुनते हैं: इस उदाहरण में, वे समान हैं और दो के बराबर हैं।
तो, समाधान विधि इस प्रकार है: अनिश्चितता को उजागर करने के लिएअंश और हर को विभाजित करना आवश्यक हैवरिष्ठ डिग्री में।
अंश और हर को से भाग दें 
ऐसा ही है, उत्तर, अनंत नहीं।
समाधान के डिजाइन में मौलिक रूप से क्या महत्वपूर्ण है?
सबसे पहले, हम अनिश्चितता का संकेत देते हैं, यदि कोई हो।
दूसरा, मध्यवर्ती स्पष्टीकरण के लिए समाधान को बाधित करना उचित है। मैं आमतौर पर एक संकेत का उपयोग करता हूं, इसका कोई गणितीय अर्थ नहीं होता है, लेकिन इसका मतलब है कि मध्यवर्ती स्पष्टीकरण के लिए समाधान बाधित किया गया था।
तीसरा, सीमा में यह चिह्नित करना वांछनीय है कि क्या प्रयास कर रहा है और कहाँ। जब काम हाथ से पूरा हो जाता है, तो इसे इस तरह करना अधिक सुविधाजनक होता है: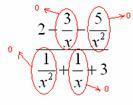 
चिह्नित करने के लिए एक साधारण पेंसिल का उपयोग करना सबसे अच्छा है।
बेशक, आप इसमें से कुछ नहीं कर सकते हैं, लेकिन फिर, शायद, शिक्षक समाधान में कमियों को नोट करेगा या असाइनमेंट पर अतिरिक्त प्रश्न पूछना शुरू कर देगा। क्या आपको इसकी जरूरत है?
उदाहरण 5
सीमा का पता लगाएं 
फिर से, अंश और हर में, हम उच्चतम घात में पाते हैं: 
अंश में अधिकतम डिग्री: 3 हर में अधिकतम डिग्री: 4 चुनें महानतममूल्य, इस मामले में एक चार। हमारे एल्गोरिथ्म के अनुसार, अनिश्चितता का खुलासा करने के लिए, हम अंश और हर को विभाजित करते हैं। असाइनमेंट का पूरा डिज़ाइन इस तरह दिख सकता है:
उदाहरण 6
सीमा का पता लगाएं 
अंश में "x" की अधिकतम डिग्री: 2 हर में "x" की अधिकतम डिग्री: 1 (इस रूप में लिखा जा सकता है) अनिश्चितता का खुलासा करने के लिए, अंश और हर को विभाजित करना आवश्यक है। एक साफ समाधान इस तरह दिख सकता है:
अंश और हर को से भाग दें
रिकॉर्डिंग का मतलब शून्य से विभाजन नहीं है (आप शून्य से विभाजित नहीं कर सकते हैं), लेकिन एक अतिसूक्ष्म संख्या से विभाजन।
इस प्रकार, प्रजातियों की अनिश्चितता का खुलासा करते समय, हम प्राप्त कर सकते हैं समापिका, शून्य या अनंत।
अभ्यास 20
जॉब नंबर 1
समाधान:यदि, चर के स्थान पर, हम 7 का मान रखते हैं, जिस पर यह प्रवृत्त होता है, तो हमें रूप की अनिश्चितता प्राप्त होती है, तो 
जॉब नंबर 2विषय: शून्य से शून्य अनिश्चितता का प्रकटीकरण
समाधान:यदि, चर के बजाय, हम मान 0 डालते हैं, जिस पर यह जाता है, तो हमें रूप की अनिश्चितता मिलती है, फिर
नौकरी # 3विषय: शून्य से शून्य अनिश्चितता का प्रकटीकरण
समाधान:यदि चर के स्थान पर हम 6 का मान रखते हैं, जिसकी ओर यह प्रवृत्त होता है, तो हमें रूप की अनिश्चितता प्राप्त होती है, तो
नौकरी # 4
समाधान:चूंकि 
तथा 
नौकरी # 5विषय: "अनंत से अनंत" रूप की अनिश्चितता का प्रकटीकरण
समाधान:चूंकि 
तथा 
तो फॉर्म की अनिश्चितता है इसे प्रकट करने के लिए, आपको अंश और हर के प्रत्येक पद को विभाजित करने की आवश्यकता है। तब, यह जानते हुए कि हम प्राप्त करेंगे: 
स्वतंत्र कार्य 20
जॉब नंबर 1विषय: शून्य से शून्य अनिश्चितता का प्रकटीकरण
जॉब नंबर 2विषय: शून्य से शून्य अनिश्चितता का प्रकटीकरण
नौकरी # 3विषय: शून्य से शून्य अनिश्चितता का प्रकटीकरण
नौकरी # 4विषय: "अनंत से अनंत" रूप की अनिश्चितता का प्रकटीकरण
नौकरी # 5विषय: "अनंत से अनंत" रूप की अनिश्चितता का प्रकटीकरणकार्य सीमा 
बराबर...
नौकरी # 6विषय: "अनंत से अनंत" रूप की अनिश्चितता का प्रकटीकरण
सीमा को हल करने के तरीके। अनिश्चितताएं।
फ़ंक्शन का विकास क्रम। प्रतिस्थापन विधि
उदाहरण 4
सीमा का पता लगाएं 
यह स्वयं करें समाधान के लिए एक सरल उदाहरण है। प्रस्तावित उदाहरण में, फिर से अनिश्चितता है (जड़ की तुलना में विकास के उच्च क्रम की)।
यदि "x" "ऋण अनंत" की ओर जाता है
"माइनस इनफिनिटी" का भूत इस लेख में काफी समय से है। उन सीमाओं पर विचार करें जिनमें बहुपद हैं। समाधान के सिद्धांत और तरीके पाठ के पहले भाग के समान ही होंगे, कई बारीकियों को छोड़कर।
व्यावहारिक कार्यों को हल करने के लिए आवश्यक 4 चिप्स पर विचार करें:
1) सीमा की गणना करें 
सीमा का मूल्य केवल अवधि पर निर्भर करता है, क्योंकि इसमें उच्चतम वृद्धि क्रम है। तो अगर असीम रूप से बड़े मोडुलोसम शक्ति के लिए ऋणात्मक संख्या, इस मामले में - चौथे में, "प्लस इनफिनिटी" के बराबर:। स्थिर ("दो") सकारात्मक, इसीलिए: 
2) सीमा की गणना करें 
यहाँ फिर से वरिष्ठ डिग्री यहाँ तक की, इसीलिए: । लेकिन "माइनस" के सामने ( नकारात्मकस्थिर -1), इसलिए: 
3) सीमा की गणना करें 
सीमा मूल्य केवल पर निर्भर करता है। जैसा कि आप स्कूल से याद करते हैं, विषम डिग्री के नीचे से "माइनस" "कूद जाता है", इसलिए असीम रूप से बड़े मोडुलोऋणात्मक संख्या से विषम घातइस मामले में "माइनस इन्फिनिटी" के बराबर है:।
स्थिर ("चार") सकारात्मक, साधन: 
4) सीमा की गणना करें
गांव का पहला लड़का फिर आया है अजीबडिग्री, इसके अलावा, छाती में नकारात्मकस्थिर, जिसका अर्थ है: इस प्रकार:
.
उदाहरण 5
सीमा का पता लगाएं 
उपरोक्त बिंदुओं का उपयोग करते हुए, हम इस निष्कर्ष पर पहुंचते हैं कि अनिश्चितता है। अंश और हर वृद्धि के एक ही क्रम के हैं, जिसका अर्थ है कि सीमा में आपको एक परिमित संख्या मिलती है। आइए जानते हैं सारे फ्राई को छोड़कर इसका जवाब: 
समाधान तुच्छ है: 
उदाहरण 6
सीमा का पता लगाएं 
यह स्वयं करें समाधान के लिए एक उदाहरण है। ट्यूटोरियल के अंत में पूरा समाधान और उत्तर दें।
और अब, शायद सबसे सूक्ष्म मामले:
उदाहरण 7
सीमा का पता लगाएं 
प्रमुख पदों पर विचार करते हुए, हम इस निष्कर्ष पर पहुँचते हैं कि अनिश्चितता है। अंश हर की तुलना में वृद्धि के उच्च क्रम का है, इसलिए आप तुरंत कह सकते हैं कि सीमा अनंत है। लेकिन कौन सा अनंत, प्लस या माइनस? तकनीक एक ही है - अंश और हर में हमें छोटी-छोटी चीजों से छुटकारा मिलता है: 
हमने निर्णय किया: 
अंश और हर को से भाग दें
उदाहरण 15
सीमा का पता लगाएं
यह स्वयं करें समाधान के लिए एक उदाहरण है। पाठ के अंत में समाप्त करने का एक मोटा उदाहरण।
परिवर्तनीय प्रतिस्थापन पर कुछ और दिलचस्प उदाहरण:
उदाहरण 16
सीमा का पता लगाएं
एक इकाई को सीमा में प्रतिस्थापित करने पर अनिश्चितता प्राप्त होती है। परिवर्तनीय प्रतिस्थापन पहले से ही स्पष्ट है, लेकिन पहले हम सूत्र का उपयोग करके स्पर्शरेखा को बदलते हैं। दरअसल, हमें स्पर्शरेखा की आवश्यकता क्यों है?
ध्यान दें, इसलिए। यदि पूरी तरह से स्पष्ट नहीं है, तो इसमें साइन मानों को देखें त्रिकोणमितीय तालिका... इस प्रकार, हम तुरंत गुणक से छुटकारा पाते हैं, इसके अलावा, हमें अधिक परिचित 0: 0 अनिश्चितता मिलती है। अच्छा होगा कि हमारी सीमा शून्य हो जाए।
आइए प्रतिस्थापित करें:
तो अगर
कोसाइन के तहत हमारे पास "x" है, जिसे "ते" के माध्यम से भी व्यक्त किया जाना चाहिए।
प्रतिस्थापन से हम व्यक्त करते हैं:।
हम समाधान पूरा करते हैं: 
(1) हम प्रतिस्थापन करते हैं
(2) कोसाइन के नीचे कोष्ठक का विस्तार करें।
(4) व्यवस्थित करना पहली अद्भुत सीमा, कृत्रिम रूप से अंश को और व्युत्क्रम से गुणा करें।
स्वतंत्र समाधान के लिए असाइनमेंट:
उदाहरण 17
सीमा का पता लगाएं
ट्यूटोरियल के अंत में पूरा समाधान और उत्तर दें।
ये उनकी कक्षा में कठिन कार्य नहीं थे, व्यवहार में सब कुछ बदतर हो सकता है, और इसके अलावा कमी सूत्र, आपको विभिन्न प्रकार के का उपयोग करना होगा त्रिकोणमितीय सूत्र, साथ ही अन्य तरकीबें। मुश्किल सीमा लेख में, मैंने कुछ वास्तविक उदाहरणों को अलग रखा =)
छुट्टी की पूर्व संध्या पर, आइए हम अंत में एक और व्यापक अनिश्चितता के साथ स्थिति को स्पष्ट करें:
अनिश्चितता का उन्मूलन "अनंत की डिग्री तक एक"
यह अनिश्चितता "सेवारत" है दूसरी अद्भुत सीमा, और उस पाठ के दूसरे भाग में, हमने समाधान के मानक उदाहरणों की बहुत विस्तार से जांच की, जो ज्यादातर मामलों में व्यवहार में सामने आते हैं। अब प्रदर्शकों के साथ चित्र पूरा हो जाएगा, इसके अलावा, पाठ के अंतिम कार्य सीमा के लिए समर्पित होंगे- "चाल", जिसमें यह लगता है कि दूसरी अद्भुत सीमा को लागू करना आवश्यक है, हालांकि यह नहीं है सभी मामले।
दूसरी उल्लेखनीय सीमा के दो कार्य सूत्रों का नुकसान यह है कि तर्क "प्लस इनफिनिटी" या शून्य पर होना चाहिए। लेकिन क्या होगा अगर तर्क एक अलग संख्या में जाता है?
बचाव के लिए एक सार्वभौमिक सूत्र आता है (जो वास्तव में दूसरी उल्लेखनीय सीमा का परिणाम है):
अनिश्चितता को सूत्र द्वारा समाप्त किया जा सकता है:
कहीं न कहीं पहले ही समझाया गया है कि वर्ग कोष्ठक का क्या अर्थ है। कुछ खास नहीं, कोष्ठक कोष्ठक की तरह हैं। वे आमतौर पर गणितीय संकेतन को स्पष्ट करने के लिए उपयोग किए जाते हैं।
आइए सूत्र के आवश्यक बिंदुओं पर प्रकाश डालें:
1) यह है केवल अनिश्चितता के बारे में और कोई नहीं.
2) "x" तर्क की प्रवृत्ति हो सकती है मनमाना मूल्य(और न केवल शून्य या), विशेष रूप से, "ऋण अनंत" या to कोईएक परिमित संख्या।
इस सूत्र का उपयोग करके आप पाठ के सभी उदाहरणों को हल कर सकते हैं। अद्भुत सीमाएंजो दूसरी उल्लेखनीय सीमा से संबंधित हैं। उदाहरण के लिए, आइए सीमा की गणना करें:
इस मामले में 
, और सूत्र द्वारा 
:
सच है, मैं आपको ऐसा करने की सलाह नहीं देता, परंपरा में यह अभी भी समाधान के "सामान्य" डिजाइन का उपयोग करने के लिए है, अगर इसे लागू किया जा सकता है। लेकिन एक सूत्र का उपयोग करना जाँच करने के लिए बहुत सुविधाजनक हैदूसरी उल्लेखनीय सीमा पर "क्लासिक" उदाहरण।
